【PyTorch][chapter 15][李宏毅深度学习][Neighbor Embedding-LLE]

明朝百晓生

已于 2024-02-09 08:46:08 修改

阅读量895

点赞数 18

文章标签：深度学习 pytorch embedding

于 2024-02-07 16:48:36 首次发布

4AM_明朝百晓生

本文链接：https://blog.csdn.net/chengxf2/article/details/136025739

版权

前言：

前面讲的都是线性降维，本篇主要讨论一下非线性降维.

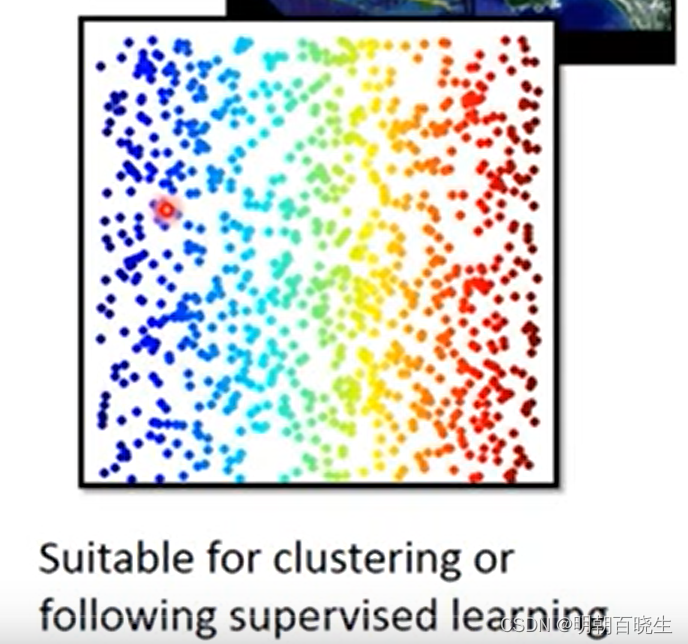
流形学习（mainfold learning）是一类借鉴了拓扑流行概念的降维方法.

如上图,欧式距离上面 A 点跟C点更近，距离B 点较远

但是从图形拓扑结构来看， B 点跟A点更近

目录：

LLE 简介
高维线性重构
低维投影
Python 例子

一局部线性嵌入（LLE Locally Linear Embedding ）

局部线性嵌入(Locally Linear Embedding，以下简称LLE)也是非常重要的降维方法。和传统的PCA，LDA等关注样本方差的降维方法相比，LLE关注于降维时保持样本局部的线性特征，由于LLE在降维时保持了样本的局部特征，它广泛的用于图像图像识别，高维数据可视化等领域。下面我们就对LLE的原理做一个总结。

1.1 LLE 思想

比如我们有一个样本 $x_1,$ 我们在它的原始高维邻域里用K-近邻算法（k=3）找到和它最近的三个样本 $x_2,x_3,x_4$ 然后我们假设 $x_1,$ 可以由 $x_2,x_3,x_4$ 线性表示，即：

$x_1=w_{12}x_2+w_{13}x_3+w_{14}x_4$ , $w_{12},w_{13},w_{14}$ 为权重系数。

在我们通过LLE降维后，我们希望 $x_1$ 在低维空间对应的投影 $z_1$ ′和 $x_2,x_3,x_4$ 对应的投影 $z_2,z_3,z_4$ 也尽量保持同样的线性关系，即

$z_1=w_{12}z_2+w_{13}z_3+w_{14}z_4$

　LLE算法的主要优点有：

　　　　1）可以学习任意维的局部线性的低维流形

　　　　2）算法归结为稀疏矩阵特征分解，计算复杂度相对较小，实现容易。

　　　　LLE算法的主要缺点有：

　　　　1）算法所学习的流形只能是不闭合的，且样本集是稠密均匀的。

　　　　2）算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响。

二高维线性重构

设有m个n维的样本

$\begin{bmatrix} x_1\\ x_2 \\ .. \\ x_m \end{bmatrix}$

使用均方差作为损失函数

$J(W)=\sum_{i=1}^{m}||x_i-\sum_{j\in Q(i)}w_{ij}x_j||_2^2$

其中：

$Q(i)$ : 按照欧式距离作为度量, 计算和样本点 $x_i$ 最近的的k个最近邻

$w_{ij}$ : 权重系数为标量， $\sum_{j \in Q(i)} w_{ij}=1$

则

$J(W)=\sum_{i=1}^{m}||x_i\sum_{j\in Q(i)}w_{ij}-\sum_{j\in Q(i)}w_{ij}x_j||_2^2$

$=\sum_{i=1}^{m}||\sum_{j\in Q(i)}w_{ij }x_i-\sum_{j\in Q(i)}w_{ij}x_j||_2^2$

$=\sum_i \sum_j ||w_{ij}(x_i-x_j)||_2^2$

$=\sum_i W_i^T(x_i-x_j)(x_i-x_j)^TW_i$

例：

设

$S_i=(x_i-x_j)(x_i-x_j)^T$ （对称矩阵）

则：

$J(w)=\sum_{i}W_i^TS_iW_i$

加上约束条件

$W_i^T1_K=1$ 其中

$1_k=\begin{bmatrix} 1\\ 1 \\ .. \\ 1 \end{bmatrix}$ k行全1的列向量

现在我们将矩阵化的两个式子用拉格朗日子乘法合为一个优化目标：

$L(W_i)=\sum_{j}W_i^TS_iW_i+\lambda(W_i^T1_k-1)$

对 $W_i$ 求导并令其值为0，我们得到

$2S_iW_i+\lambda 1_k=0$ (前半部分利用了 $S_i$ 的对称性简化了)

$W_i=\frac{-\lambda}{2}(S_i)^{-1}1_k$ （公式1）

$=\frac{S_i^{-1}1_k}{1_k^TS_i^{-1}1_k}$ (公式2)

公式2的解原理

由约束条件: $W_i^T1_K=1$ ， $1_k^TW_i=1$

已知： $W_i=\frac{-\lambda}{2}(S_i)^{-1}1_k$

则

$1_k^TW_i=1$

$1_k^T\frac{-\lambda}{2}S_i^{-1}1_k=1$

$\frac{-\lambda}{2}=1/(1_k^TS_i^{-1}1_k)$

重新带入公式1 ,即得到公式2

$W_i=\frac{S_i^{-1}1_k}{1_k^TS_i^{-1}1_k}$

三低维投影

我们得到了高维的权重系数W，那么我们希望这些权重系数对应的线性关系在降维后的低维一样得到保持。假设我们的n维样本集{ $x_1,x_2,...x_m$ }在低维的d维度对应投影为{ $z_1,z_2,...z_m$ }, 则我们希望保持线性关系，也就是希望对应的均方差损失函数最小，即最小化损失函数J(Y)如下：

$J(z)=\sum_{i=1}^{m}||z_i-\sum_j^{m}w_{ij}z_j||_2^2$

注意：

低维的损失函数中：权重系数W已知，目标是求最小值对应的数据z

W: 是[m,m]矩阵，我们将那些不在邻域位置的 $W_i$ 的位置取值为0，将W扩充到m×m维度。

一般我们也会加入约束条件如下：

$\sum_{i=1}^{m}z_i=0$

$\frac{1}{m}\sum_{i=1}^{m}z_iz_i^T=E$ : 单位矩阵

3.1 原理推导

$Z\sim R^{d*m}$

损失函数为

$J(Z)=\sum_{i=1}^{m}||z_i-\sum_{j}^{m}W_{ij}z_j||_2^2$

$=\sum_{i=1}^{m}||ZE_i-ZW_i||_2^2$ (步骤一）

$=\sum_{i=1}^{m}||Z(E_i-W_i)||_2^2$

$=tr(Z(E-W)(E-W)^TZ^T)$

备注：步骤一原理

其中 $I_i, W_i$ 为m 行一列的列向量

下面一步推导用到了该知识:

$tr(aa^T)=\sum_{i=1}^{m}a_i^2$

$a=\begin{bmatrix} a_1\\ a_2 \\ .... \\ a_m \end{bmatrix}$

设

$M=(E-W)(E-W)^T$

$J(Z)=tr(ZMZ^T)$

加上约束条件,得到拉格朗日函数

$L(Z)=tr(ZMZ^T+\lambda(ZZ^T-mE))$

对Z 求微分

$2MZ^T+2\lambda Z^T=0$

$MZ^T=\lambda^{'} Z^T$

要得到最小的d维数据集，我们需要求出矩阵M最小的d个特征值所对应的d个特征向量组成的矩阵 $Z=(z_1,z_2,..z_d)$

由于M的最小特征值为0不能反应数据特征，此时对应的特征向量为全1。我们通常选择M的第2个到第d+1个最小的特征值对应的特征向量

2.2 为什么M的最小特征值为0呢？

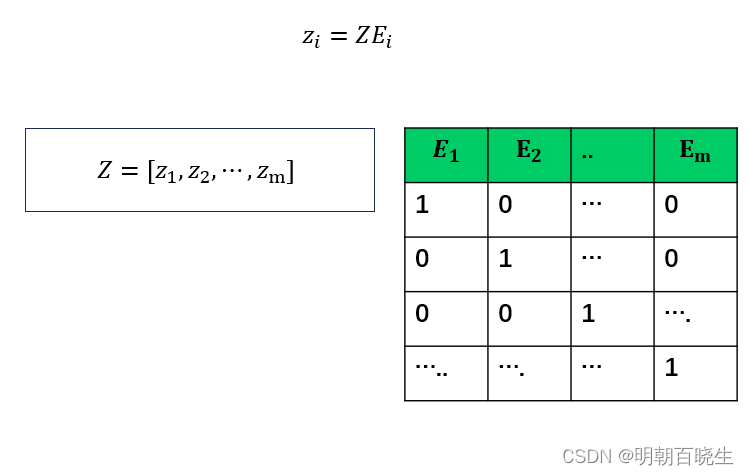
前面知道约束条件： $W^Te=1*e$ ,

$(W^T-E)e=0$ (注意大E和小e 不一样,前面是单位矩阵，后面是全1的列向量）

$(E-W^T)e=0$

$(E-W)(E-W^T)e=0*(E-W)=0$

$(E-W)(E-W^T)e=0*e$

所以最小的特征值为0,对应的特征向量为全1的列向量。

把该最小特征值丢弃

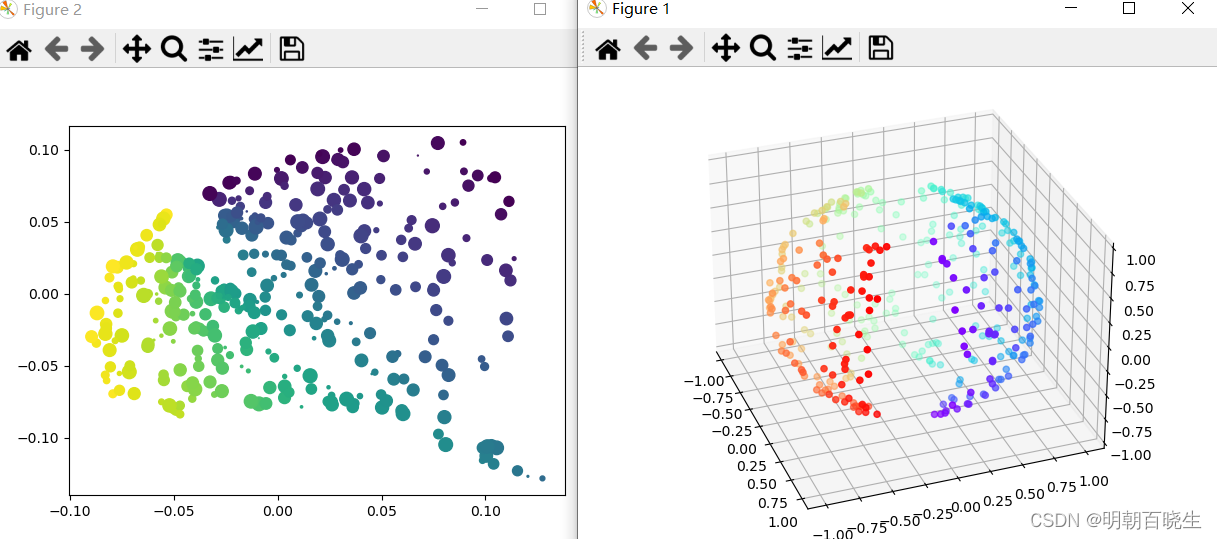
$W^T=\begin{bmatrix} W_1^T\\ .... \\ W_i^T\\ ....\\ W_m^T\end{bmatrix}$ $e=\begin{bmatrix} 1\\ 1 \\ ... \\ 1 \end{bmatrix}$ $W_1^Te=1,W_2^Te=1,..W_i^T=e$

四 Python 例子

# -*- coding: utf-8 -*-
"""
Created on Wed Feb  7 17:02:55 2024

@author: chengxf2
"""

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import manifold, datasets
from sklearn.utils import check_random_state


def generateData(m = 500):
    
    random_state = check_random_state(0)
    p = random_state.rand(m) * (2 * np.pi - 0.55)
    t = random_state.rand(m) * np.pi

    # 让球体不闭合，符合流形定义
    indices = ((t < (np.pi - (np.pi / 8))) & (t > ((np.pi / 8))))
   
    colors = p[indices]
    x, y, z = np.sin(t[indices]) * np.cos(p[indices]), \
    np.sin(t[indices]) * np.sin(p[indices]), \
    np.cos(t[indices])

    fig = plt.figure()
    
   
    ax = Axes3D(fig, elev=30, azim=-20,auto_add_to_figure=False)
    fig.add_axes(ax)
    ax.scatter(x, y, z, c=p[indices], marker='o', cmap=plt.cm.rainbow)
    plt.show()
 

    return x,y,z,colors


def LLE():
    
    x,y,z,colors= generateData()
    
    train_data = np.array([x,y,z]).T
    print("\n 高维空间shape",np.shape(train_data))
    #n_neighbors: 高维空间K邻近选择的点个数
    #n_components：低维空间的维度

    #[362,2]
    trans_data = manifold.LocallyLinearEmbedding(n_neighbors =10, n_components = 2,
                                method='standard').fit_transform(train_data)
    print("\n 低维空间shape",np.shape(trans_data))
  
    size = np.random.rand(363)*100
    fig = plt.figure()
    plt.scatter(trans_data[:, 0], trans_data[:, 1],s=size, marker='o',c=colors)

    
LLE()

参考：

15: Unsupervised Learning - Neighbor Embedding_哔哩哔哩_bilibili

https://www.cnblogs.com/pinard/p/6266408.html

明朝百晓生

关注

18
点赞
踩
15

收藏

觉得还不错? 一键收藏
0
评论
【PyTorch][chapter 15][李宏毅深度学习][Neighbor Embedding-LLE]

和传统的PCA，LDA等关注样本方差的降维方法相比，LLE关注于降维时保持样本局部的线性特征，由于LLE在降维时保持了样本的局部特征，它广泛的用于图像图像识别，高维数据可视化等领域。我们得到了高维的权重系数W，那么我们希望这些权重系数对应的线性关系在降维后的低维一样得到保持。要得到最小的d维数据集，我们需要求出矩阵M最小的d个特征值所对应的d个特征向量组成的矩阵。2）算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响。1）算法所学习的流形只能是不闭合的，且样本集是稠密均匀的。
复制链接

扫一扫