奇异值矩阵分解(Singular Value Decomposition)的一些感想

写在前面的话：

最近的大半年一直在和矩阵分解和数值运算打交道，基本功不扎实吃了很多亏。

主要是在做算法的研究和优化。核心算法里需要用到矩阵分解的思想，目前广泛应用的分解方式有整数分解，特征值分解(eigen value)，奇异值分解(SVD)，非负矩阵分解(non-negative matrix fatorization)等等。我整个学习和使用的过程比较艰辛，走了很多弯路，因为之前完全把分解算法当做黑盒来处理，并没有深入进去算法的本质。而本文作为一个记录，回顾一下我学习过程的一些思考，以及一部分自己的见解。

本文主要分为五部分，在目录中有介绍，正文部分写的比较凌乱，因为记录了自己思考的整个过程，思维混乱是做研究的大忌，所以以后要改正，特别是需要静下心来慢慢梳理的部分。好在SVD的学习曲线不算非常陡峭，因而可以充分的边学边思考。目前许多大型的算法在建立之后(比如大部分的推荐算法以及计算广告等)都会划归为矩阵的操作，这里面有普通的数值运算，也有复杂的分解和变换。而奇异值分解(SVD)就是这其中效果很好并广为使用的一种，SVD的一个代数特性就是它用到了几乎所有的线性代数知识，把线性代数从入门到进阶的基础知识完美的串联了起来，推导逐层深入，理解逐渐细化。所以当你对SVD了然于心的时候，不知不觉之间，线性代数的基础知识也更加稳固了。

--------------------------------------------------------------------------------------------------------------------

content

背景

1. 什么是SVD

     - concept

     - geometry/physical  aspect

2. SVD实现

     - conventional algorithm

3. 算法优化

     - modify: compute the largest singular value

4. MATLAB的实现

5. SVD的应用

     - Rank

     - PCA

     - image denoise

     - video deblocking 

     - recommender system

--------------------------------------------------------------------------------------------------------------------

背景

最近几个月一直在做一些有关奇异值分解(SVD，Singular Value Decomposition)的东西，并没有从理论上创新的修改奇异值的计算方法，只是在学习和了解的过程中逐渐明白了SVD的一些意义和实际的应用场景。学习的过程中间走了很多弯路，也有了很多不理解的地方，到现在也不敢说是完全明白，但是我觉得有必要总结一下这一系列的东西，顺便也梳理一下研究的思路，不要因为走得太远而忘记了为了什么而出发。同时在知乎上也有一个这类的问题[1]，但是个人觉得高票的几个回答从不同的角度在解释这个问题，所以尝试自己写一个比较简单的问题。

1. 什么是SVD

1.1 概念

SVD是Singular Value Decomposition的缩写，翻译成中文一般是奇异值分解。这是一种矩阵分解形式，它将一个矩阵(可以是实矩阵也可以是复矩阵，我们只讨论实矩阵)分解为三个子矩阵，分别代表了左奇异向量，奇异值矩阵以及右奇异向量。直接说概念可能会比较抽象，后面会详细的介绍各个矩阵的左右以及物理意义。除了奇异值分解，目前常用的矩阵分解方式还有根据特征值分解以及非负矩阵分解(Non-negative Matrix Factorization, NMF)。如果需要回忆一些线性代数的基础知识的话，可以参考[2]网易公开课上MIT的线性代数课程， Gilbert Strang将很多线性代数的基础知识讲的深入浅出，个人强推。

那么，奇异值的数学表达式是什么呢？对于矩阵X，总能找到一个正交矩阵U和一个正交矩阵V，以及一个对角矩阵 Σ，使得：

X = UΣV ^T

式子成立。其中，U被称为的左奇异向量，V被称为右奇异向量，而对角矩阵 Σ的主对角线上的值称为矩阵X的奇异值，并按照从大到小降序排列。

1.2 几何意义

以2x2的矩阵为例，因为二阶矩阵可以使用平面在直角坐标系来表示，主要参考了[3]。SVD在2x2矩阵上的作用的几何意义主要是可以将二维空间下两个互相正交(也就是垂直)的向量，通过矩阵分解，变换为另一个二维空间下互相正交的两个向量。具体的过程如下图所示。

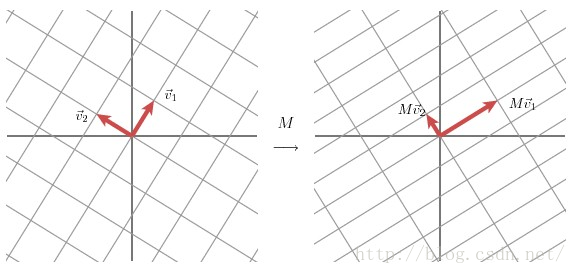
上图的含义是，我们在左图首先选定了两个单位正交基向量 V 1和 V ₂  。那么此时，通过矩阵M的作用下，左图中的一个二维空间(左图正方形格子)下的正交向量 V 1和 V ₂  。就变换成为了另一个二维空间(右图长方形格子)下的正交向量Mv 1和 Mv ₂   。然后我们在 Mv 1和 Mv ₂ 的方向上分别选择两个单位向量 u₁ 和 u_{2 ，}同时设 Mv 1和