文章目录
修订20230426,之前还是没有把注意力说清楚。今天试图重新整理文章。
修订20240319,多头注意力增加图片解释
文章目录
何为注意力?
面对纷繁复杂的信息,我们试图找出最重要的部分,可以称之为注意力机制,就是一种“简化数据的方法”,或者说是“信息选择方式”。
♠自下而上的基于显著性的注意力机制
其实:最大汇聚(max pooling)、门控(gating)这些算法(算子、机制)可以近似地看作是自下而上的基于显著性的注意力机制。我们从输出的特征做注意力。因此是自下而上的。
♥自上而下的会聚式注意力——attention
自上而下的会聚式注意力也是一种有效的信息选择方式。我们从原始信息入手做注意力,因此是自上而下的。我们一般认为这就是attention机制了。
1 首先,什么是 attention 注意力机制?
这就是一种计算方法,实现有效信息选择的方式。
2 然后attention 算子的计算方法
2.1 简单理解
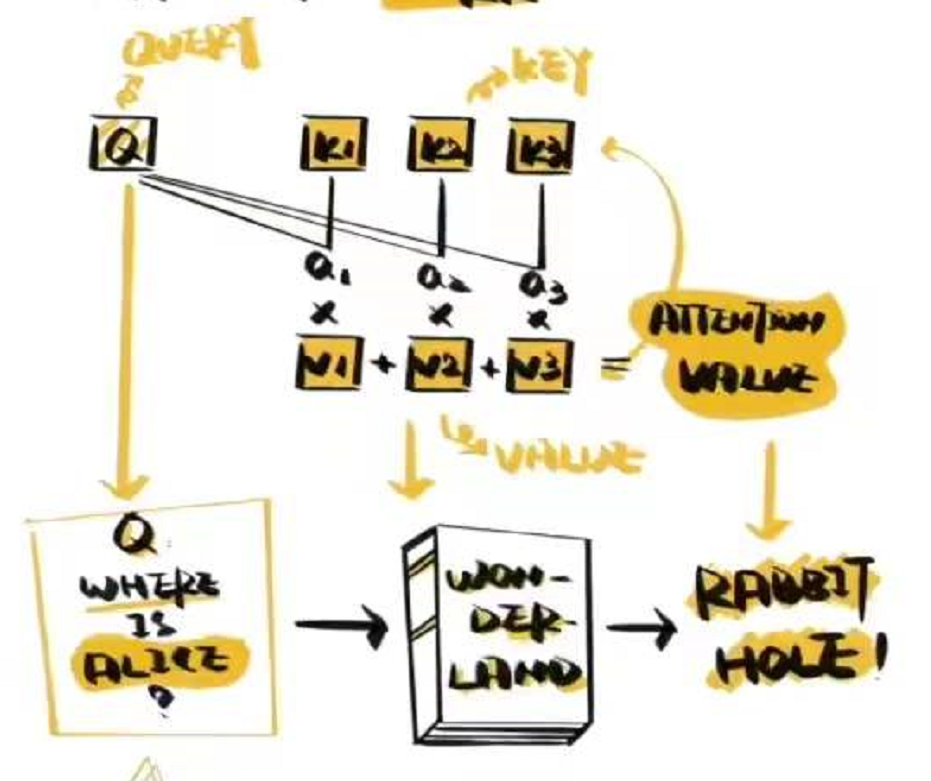
一个典型的Attention 包含三个部分 Q K V
Q 是query 是输入的信息
K 是Key ,V是value,K和V成组出现。通常是源语言,原始文本等已有信息。通过计算Q和K之间的相关性,得到a, 得出不同的K 对输出的重要程度再与对应的V 相乘求和,就得到了Q 的输出。
Output = F(Q)
举个例子
以阅读理解为例子,
Q是问题:Where is Alice?
K和V是原始文本:Wonder Land,
然后我们计算Q和K 的相关性,让我们找到文本中最需要注意的部分;然后利用 V 得到答案。
2.2 详细公式化理解
2.2.1 注意力的概率计算函数
这个函数的目的是:计算Q和 X的相关性。
用X=(x_1,x_2,…,x_N)表示N个输入信息,给定一个和任务相关的查询(Query)向量q,用z=1,2,…,N表示被选择信息索引位置,则第i个输入信息的概率(也称为注意力分布)

其中s(x_i,q)为注意力打分函数,一般采用缩放点积形式来定义:

其中d为输入信息的维度。
2.2.2 attention的计算函数
这个函数的目的是:我们计算Q和K 的相关性,让我们找到文本中最需要注意的部分;然后利用 V 得到答案。
输入信息存储在键值对(Key-Value pairs)中:(K, V)=[(k_1,v_1),…,(k_n,v_n)],则当q已知,注意力

3 不同类型的算子
3.1 自注意力:
只关注输入序列元素之间的关系。通过将输入序列直接转化成为Q K V ,在内部进行attention 计算,很好的捕捉文本内在的联系,对其做出再表示,输出Y1 Y2 Y3 Y4

为何会提出这个算子?
因为:
1、CNN或RNN只能表征输入信息的短距离相关
2、引入门控机制的LSTM,所表征的也只是一种“长的短期记忆”(long short-term memory),换言之,LSTM只能表征与其结构如榫卯般契合的、特定的长距离相关。
3、全连接网络是一种非常直接的建模远距离依赖的模型,但是无法处理变长的输入序列。不同的输入长度,其连接权重的大小也是不同的。
因此:
对于不同的输入长度,这时我们就可以利用注意力机制来“动态”地生成不同连接的权重,使得权重与数据本身的重要性相关。
公式化表述
输入的Q K V 都来源于 原始文本 X。

这里的Q,K,V都是通过X做线性变换得到,权重矩阵WQ,WK,WV可以通过注意力来动态地调整。因此称为自注意力(self-attention)。
输出向量

写成矩阵形式为

3.2 多头注意力机制,
在自注意力机制上,使用多种变换生成Q K V 进行计算,在将他们对相关性的结论综合起来,进一步增强Self-Attention 的效果。Multi-head机制,通过多个查询Q=[q_1,…,q_M]计算注意力函数

多头注意力(Multi-Head Attention)是注意力机制的一种扩展形式,可以在处理序列数据时更有效地提取信息。
在标准的注意力机制中,我们计算一个加权的上下文向量来表示输入序列的信息。而在多头注意力中,我们使用多组注意力权重,每组权重可以学习到不同的语义信息,并且每组权重都会产生一个上下文向量。最后,这些上下文向量会被拼接起来,再通过一个线性变换得到最终的输出。
多头注意力是Transformer模型中的一个重要组成部分,被广泛用于各种自然语言处理任务,如机器翻译、文本分类等。

不同算法形式
基于注意力机制,有不同的算法形式。
1、Transformer
有机会写文章讲解这些不同算法形式


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










