标准二阶响应--佛朗哥

最新推荐文章于 2024-05-31 09:55:17 发布

薛定谔的猫~~~

最新推荐文章于 2024-05-31 09:55:17 发布

阅读量462

点赞数

文章标签：硬件工程

本文链接：https://blog.csdn.net/estzmj/article/details/129746335

版权

如果一个电路对任何有界输入在响应中产生一个有界的输出，就说明这个电路是稳定的。判断一个电路是否稳定一种方法是将某些能量注入到它的电抗元件中的一个或者多个，然后在没有任何外加电源的情况下观察这个电路是如何作为的。这种情况下的响应为无源或者自然响应。注入能量的一种办法即为冲击响应，它的拉普拉斯变换是1，所得到的响应 $h\left ( t \right )=\varphi ^{-1}\left \{ H\left ( s \right ) \right \}$ ；这个响应是由极点决定的。

1） $H\left ( s \right )$ 有一个极点在 $s=\sigma _{k}\pm j0=\sigma _{k}$ ，可以得知 $H\left ( s \right )$ 含有 $A_{k}/\left ( s-\sigma _{k} \right )$ ， $A_{k}$ 为 $H\left ( s \right )$ 在那个点的留数。可以得出 $A_{k}=\left ( s-\sigma _{k} \right )H\left ( s \right )\mid _{s=\sigma _{k}}$ ；由拉普拉斯反变换可以推出：

$\varphi ^{-1}\left \{ \frac{A_{k}}{s-\sigma _{k}} \right \}=A_{k}e^{\sigma _{k}t}u\left ( t \right )$ ；其中 $u\left ( t \right )$ 是单位阶跃函数（u=0，t<0；u=1，t>0）；一个实数极点对响应 $x_{o}\left ( t \right )$ 贡献指数分量。若 $\sigma _{k}$ <0，分量衰减； $\sigma _{k}$ =0，分量不变； $\sigma _{k}$ >0，响应将发散。

2） $H\left ( s \right )$ 若有复数极点，即都是共轭存在的， $s=\sigma _{k}\pm jw_{k}$ ，则其中一个留数 $A_{k}=\left ( s-\left ( \sigma _{k}+jw_{k} \right ) \right )H\left ( s \right )\mid s=\sigma _{k}+jw_{k}$ ；另一个共轭的留数同理可以得出。则他们组合的拉普拉斯变换 $\varphi ^{-1}\left \{ \frac{A_{k}}{s-\left ( \sigma _{k} +jw_{k}\right )}+\frac{A_{k}^{*}}{s-\left ( \sigma _{k} -jw_{k}\right )} \right \}=2\left | A_{k} \right |e^{\sigma _{k}t}u\left ( t \right )cos\left ( w_{k}t+\nless A \right )$ ；同理若 $\sigma _{k}$ <0，分量衰减的正弦； $\sigma _{k}$ =0，恒定振幅的正弦； $\sigma _{k}$ >0，幅度增长的正弦。

很清楚，若要电路稳定，则全部极点位于s平面的左半平面。

二阶响应，即传递函数的分母的阶数是2，除了 $w_{0}$ 外还有一个附加的滤波器参数，所有的二阶函数都可以表示成如下的标准形式：

$H\left ( s \right ) = \frac{N\left ( s \right )}{\left ( s/w_{0} \right )^{2}+2\zeta \left ( s/w_{0} \right )+1}$

其中分子N(s)是一个阶次m $\leq$ 2的多项式。 $w_{0}$ 称为无阻尼自然频率，单位为rad/s。而 $\zeta$ 是阻尼系数。根据一元二次方程的求解，分母为0有两个解。即极点 $p_{1,2}$ = $\left ( -\zeta \pm \sqrt{\zeta ^{2}-1} \right )w_{0}$ ，

1）当 $\zeta >1$ 时，极点为实数且为负。自然响应是由两个衰减的指数项组成，称为过阻尼。

2）当 $0<\zeta <1$ 时，极点为一对共轭复根， $P_{1,2}=-\zeta w_{0}+jw_{0}\sqrt{1-\zeta ^{2}}$ ，欠阻尼。

3）当 $\zeta =0$ 时， $P_{1,2}=\pm jw_{0}$ ；这些极点都位于虚轴上，自然响应是一个恒定不变未受衰减的正弦函数，它的频率是 $w_{0}$

4）当 $\zeta <0$ 时，发散。

令 $s\rightarrow jw$ 可以得到频率响应，可以通过另外一个无量纲参数Q将频率响应改为：

$H\left ( jw \right )=\frac{N\left ( jw \right )}{1-\left ( w/w_{0} \right )^{2}+\left ( jw/w_{0}/Q \right )}$ ； $Q=\frac{1}{2\zeta }$ ；

1. 低通响应 $H_{LP}$

所有的二阶低通函数都可以表示成 $H\left ( jw \right )=H_{0LP}H_{LP}\left ( jw \right )$ ；其中 $H_{0LP}$ 是一个常数，为直流增益。 $H_{LP}\left ( jw \right )=\frac{1}{1-\left ( w/w_{0} \right )^{2}+\left ( jw/w_{0} \right )/Q}$

1)当 $w/w_{0}\ll 1$ 时，分母中第二项与第三项忽略。 $H_{LP}\rightarrow 1$ 。 $\left | H_{LP} \right |_{dB}=0$ ；

2)当 $w/w_{0}\gg 1$ 时，分母只考虑第二项。 $H_{LP}\rightarrow -1/\left ( w/w_{0} \right )^{2}$ ，那么 $\left | H_{LP} \right |_{dB}=20log_{10}\left ( 1/\left ( w/w_{0} \right )^{2} \right )=-40log_{10}\left ( w/w_{0} \right )$ ;即属于y=-40x类型，斜率为-40dB/dec的直线。与一阶相比更陡峭。

3)当 $w/w_{0}=1$ 时，两条线相交， $H_{LP}=-jQ\; \; \; \left | H_{LP} \right |_{dB}=Q_{dB}$ ；在靠近 $w/w_{0}=1$ 的频率范围内，得到一组依赖于Q值的曲线簇。在实际应用中，Q的范围可以为0.5~100，而接近于1的那些值最为常用。对于低Q值，从一条渐近线到另一条的过渡是平缓的，而对于高Q值，有 $\left | H_{LP} \right |> 1$ ，这种现象称为峰化。根据 $\left | H_{LP} \right |_{dB}=\frac{1}{\sqrt{\left ( 1-\left ( w/w_{0}\right ) ^{2}\right )^{2}+\left (( w/w_{0}\right )/Q)^{2}}}$ ，将 $\left (w/w_{0} \right )^{2}$ 当成一元，为了使 $\left | H_{LB} \right |$ 最大，即使得分母最小，抛物线的最低端，即 $\left (w/w_{0} \right )^{2}$ = $\frac{-b}{2a}$ 时最小。峰化之前Q最大值是Q=1/ $\sqrt{2}$ =0.707。它对应的曲线是最大平坦或者巴特沃滋响应，当Q>1/ $\sqrt{2}$ 时， $\left | H_{LB} \right |$ 取最大值时的频率及对应的最大值为：

$w/w_{0}=\sqrt{1-1/2Q^{2}}$ $\left | H_{LP} \right |=\frac{Q}{\sqrt{1-1/4Q^{2}}}$

对于足够大的Q，比如Q>5，有 $w/w_{0}\cong 1\, \, \, \, \left | H_{LP} \right |_{max}\cong Q$ ；若没有峰值存在，即 $Q< 1/\sqrt{2}$ ，那么在 $w/w_{0}=0$ 时最大，即为直流时。

$H_{LP}\left ( j0 \right )=H_{0LP}\, \, \, H_{LP}\left ( jw_{0} \right )=-jH_{0LP}Q$ ；寻找这样的一个频率，在这个频率上，输出信号相对于输入信号有90°的相移，从而测得出 $w_{0}$ ，利用 $Q=\left | H_{LP}\left ( jw_{0} \right ) \right |/\left | H_{0LP} \right |$ 即可以测出Q。

2. 高通响应 $H_{HP}$

所有二阶高通函数的标准形式是 $H\left ( jw \right )=H_{0HP}\frac{-\left ( w/w_{0} \right )^{2}}{1-\left ( w/w_{0} \right )^{2}+j\left ( w/w_{0} \right )/Q}$ ， $H_{0HP}$ 称为高频增益，令 $jw\rightarrow s$ ，表明 $H\left ( s \right )$ 除了有一对极点，原点还有一个二阶零点，把 $H_{LP}\left ( jw/w_{0} \right )$ 中的 $\left ( jw/w_{0} \right )$ 换成 $1/\left ( jw/w_{0} \right )$ 就可以得到 $H_{HP}\left ( jw/w_{0} \right )$ ， $H_{HP}$ 的幅度图是 $H_{LP}$ 幅度图的镜像。

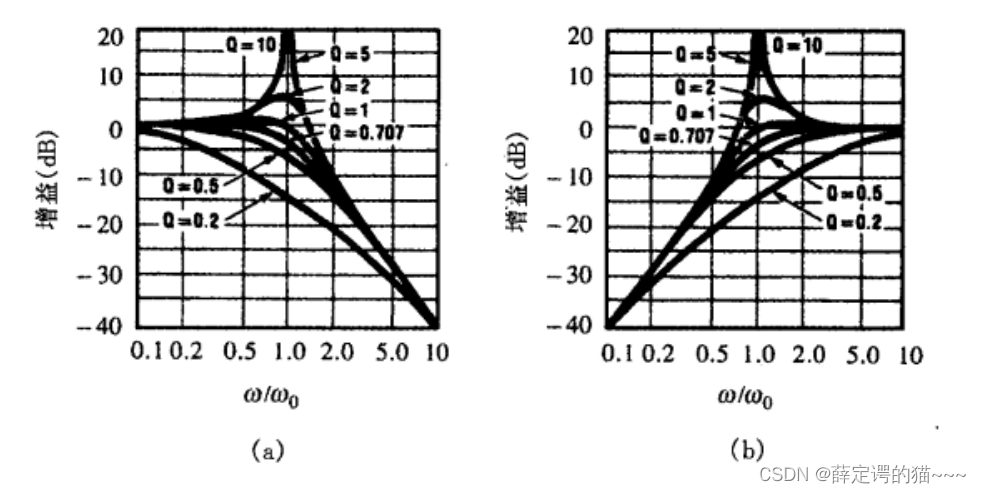
3. 带通响应 $H_{BP}$

所有二阶带通函数的标准形式是 $H\left ( jw \right )=H_{0BP}H_{BP}\left ( jw \right )$ ，式中 $H_{0BP}$ 称为谐振增益，而

$H_{_{BP}}\left ( jw \right )=\frac{\left ( jw/w_{0} \right )/Q}{1-\left ( w/w_{0} \right )^{2}+\left ( jw/w_{0} \right )/Q}$ ，这个函数除了有一对极点外，在原点还有一个零点。

1)当 $w/w_{0}\ll 1$ 时，分母中第二项与第三项忽略。 $H_{BP}\rightarrow \left ( jw/w_{0} \right )/Q$ ，因此低频渐近线为

$\left | H_{BP} \right |_{dB}=20log\left [ \left ( w/w_{0} \right ) /Q\right ]=20log\left [ \left ( w/w_{0} \right ) \right ]-Q_{dB}$ 。这个方程属于 $y=20x-Q_{dB}$ 的类型，表明一条斜率为20dB/dec的直线，但在 $w/w_{0}$ =1处，相对于0dB轴有一个 $-Q_{dB}$ 的位移。

2)当 $w/w_{0}\gg 1$ 时，分母只考虑第二项。 $H_{BP}\rightarrow -j1/\left ( w/w_{0} \right )Q$ ，因此高频渐近线为

$\left | H_{BP} \right |dB=-20log\left ( w/w_{0} \right )-Q_{dB}$ 这与上面有相同位移量的直线，但它的斜率是-20dB/dec。

3)当 $w/w_{0}=1$ 时， $H_{BP}=1\rightarrow \left | H_{BP} \right |dB=0$ ；无论Q取何值时， $\left | H_{BP} \right |$ 在 $w/w_{0}=1$ 处最大，称为峰值或谐振频率。

所有曲线的峰值都是0dB，对应不同的Q值，曲线形状有差别。对于高Q值，形状窄，有较高的选择性，低Q值，形状宽。高选择性曲线斜率滚降到 $\pm 20dB/dec$ ，但在 $w/w_{0}=1$ 附近时，这些曲线的斜率比 $\pm 20dB/dec$ 更为陡峭。带宽BW= $w_{H}-w_{L}$ ，其中 $w_{L}$ 和 $w_{H}$ 都是-3dB频率。

由以上式子在-3dB时可推算出 $w_{L}$ 和 $w_{H}$ ，

$H_{_{BP}}\left ( jw \right )=\frac{\left ( jw/w_{0} \right )/Q}{1-\left ( w/w_{0} \right )^{2}+\left ( jw/w_{0} \right )/Q}$ ， $\rightarrow \left | H_{BP} \right |=\frac{1}{\sqrt{2}}$

$\frac{\left ( w/w_{0}Q \right )}{\sqrt{\left ( 1-\left ( w/w_{0} \right )^{2} \right )^{2}+\left ( w/w_{0}Q \right )^{2}}}=\frac{1}{\sqrt{2}}$ ，两边取平方可推出 $\left ( 1-\left ( w/w_{0} \right )^{2} \right )^{2}=\left ( w/w_{0}Q \right )^{2}$

$\Rightarrow$ $1-\left ( w/w_{0} \right )^{2}=\pm \left ( w/w_{0}Q \right )$ $\Rightarrow$ 根据一元二次方程求解 $w/w_{0}=\sqrt{1+1/4Q^{2}}\pm 1/2Q$

得 $w_{L}=w_{0}\left ( \sqrt{1+1/4Q^{2}} -1/2Q\right )\, \, \, \, w_{H}=w_{0}\left ( \sqrt{1+1/4Q^{2}} +1/2Q\right )$ ； $w_{0}=\sqrt{w_{L}w_{H}}$ ；

$w_{0}$ 是 $w_{L}$ 和 $w_{H}$ 的几何均值。在对数坐标上 $w_{0}$ 是 $w_{L}$ 和 $w_{H}$ 的中点，显然带宽越窄，滤波器的选择越好，然而选择性还是依赖于 $w_{0}$ ，BW=10rad/s和 $w_{0}$ =1k rad/s的滤波器选择性明显优于 BW=10rad/s和 $w_{0}$ =100 rad/s的滤波器，一种有效的度量是求 $w_{0}$ /BW的比值，根据以上式子 $w_{H}$ - $w_{L}$ 可以得出 $Q=w_{0}/BW$ 。

$H_{BP}\left ( jw_{0} \right )=H_{0BP}$ ， $\nless H_{BP}\left ( jw_{L} \right )=\nless H_{0BP}-45^{o}$ ， $\nless H_{BP}\left ( jw_{H} \right )=\nless H_{0BP}-135^{o}$ ；通过测量 $w_{L}$ 和 $w_{H}$ ，在这些频率上输出对输入有正负45°的

4. 带阻响应 $H_{N}$

最常用的形式是 $H\left ( jw \right )=H_{0N}H_{N}\left ( jw \right )$ ， $H_{0N}$ 是一个常数。

$H_{N}\left ( jw \right )=\frac{1-\left ( w/w_{0} \right )^{2}}{1-\left ( w/w_{0} \right )^{2}+jw/w_{0}Q}$ ，令jw $\rightarrow$ s，可得出该函数有一对极点和一对零点， $z_{1,2}=\pm jw_{0}$ ；可以看出在相当低或者相当高的频率上， $H_{N}\rightarrow 1$ ，对于 $w/w_{0}=1$ 时， $\left | H_{N} \right |_{dB}\rightarrow -\infty$ ，Q值越高，带阻曲线越窄， $w_{0}$ 称为隔波频率。 $H_{N}=H_{LP}+H_{HP}=1-H_{BP}$

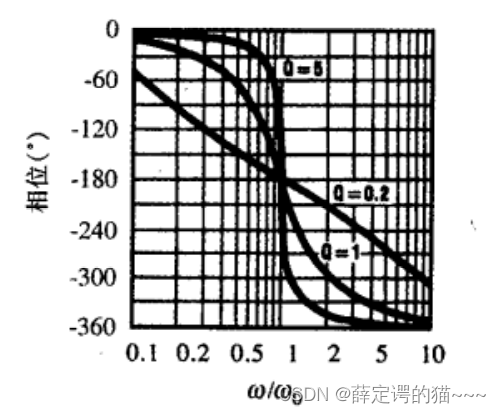
5. 全通响应

最常用的形式是 $H\left ( jw \right )=H_{0AP}H_{AP}\left ( jw \right )$ ， $H_{0AP}$ 是一个常数；

$H_{AP}\left ( jw \right )=\frac{1-\left ( w/w_{0} \right )^{2}-jw/w_{0}Q}{1-\left ( w/w_{0} \right )^{2}+jw/w_{0}Q}$ ；这个函数有两个零点和两个极点。关于jw轴对称。无论频率为何值时，都有 $\left | H_{AP} \right |=1\, \, \, \, \left | H_{AP} \right |_{dB}=0dB$ 。