投资组合：使用加权均值和协方差估计器的投资组合优化

已于 2024-04-25 14:35:11 修改
阅读量79 收藏
点赞数
分类专栏： 投资组合 文章标签： 算法 金融 python
于 2024-04-24 23:01:36 首次发布
原文链接：https://financialnoob.me/portfolio-optimization-with-weighted-mean-and-covariance-estimators/
版权

投资组合：使用加权均值和协方差估计器的投资组合优化

github仓库地址：https://github.com/financialnoob/portfolio_optimization
原文链接：https://financialnoob.me/portfolio-optimization-with-weighted-mean-and-covariance-estimators/

系列文章

  1. 投资组合优化核现代投资组合理论
  2. 使用加权均值和协方差估计器的投资组合优化
  3. 利用随机矩阵理论估计协方差矩阵的投资组合优化

文章目录

前言

现代投资组合理论（MPT）的假设之一是，收益的均值和协方差矩阵是已知的。显然，实际情况并非如此，我们必须使用某些估计值。使用的估计值的准确性对结果投资组合有很大影响。在之前的文章中，我使用了在滚动窗口中计算出的样本均值和协方差。在本文中，我将尝试通过使用加权估计器来提高最优投资组合的表现。本文基于论文《估计协方差矩阵》（Litterman, Winkelmann 1998），该论文描述了当时在高盛使用的估计框架。

论文的第二部分展示了在金融数据中发现的几个实证规律：

  • 波动性是时变的。
  • 相关性是时变的。
  • 金融数据具有厚尾特性。

厚尾特性（Fat-tails）是统计分布的一个特征，它描述的是数据分布的尾部（即非中心部分，通常是极端值所在的区域）比标准正态分布的尾部“厚”或“重”。在厚尾分布中，发生极端事件的概率比正态分布中的概率要高。

波动性

让我们看看这些规律是否存在于近期数据中。

首先我将观察波动性。我将使用从2018年1月1日到2022年12月31日的SPY ETF回报进行比较。我将比较使用所有可用数据计算出的历史标准差与100天滚动标准差。下面提供了执行此操作的代码。

spy = yf.download('SPY', start='2018-01-01', end='2022-12-31')['Adj Close']
spy_ret = spy.pct_change().dropna()
spy_hist_std = spy_ret.std()*np.sqrt(252) # 年化历史标准差
spy_rolling_std = spy_ret.rolling(100).std().dropna()*np.sqrt(252) # 年化滚动标准差（100天）

plt.figure(figsize=(18,6))
plt.plot(spy_rolling_std, label='100-day rolling')
plt.axhline(spy_hist_std, label='historical', color='m', linestyle='dashed')
plt.legend()

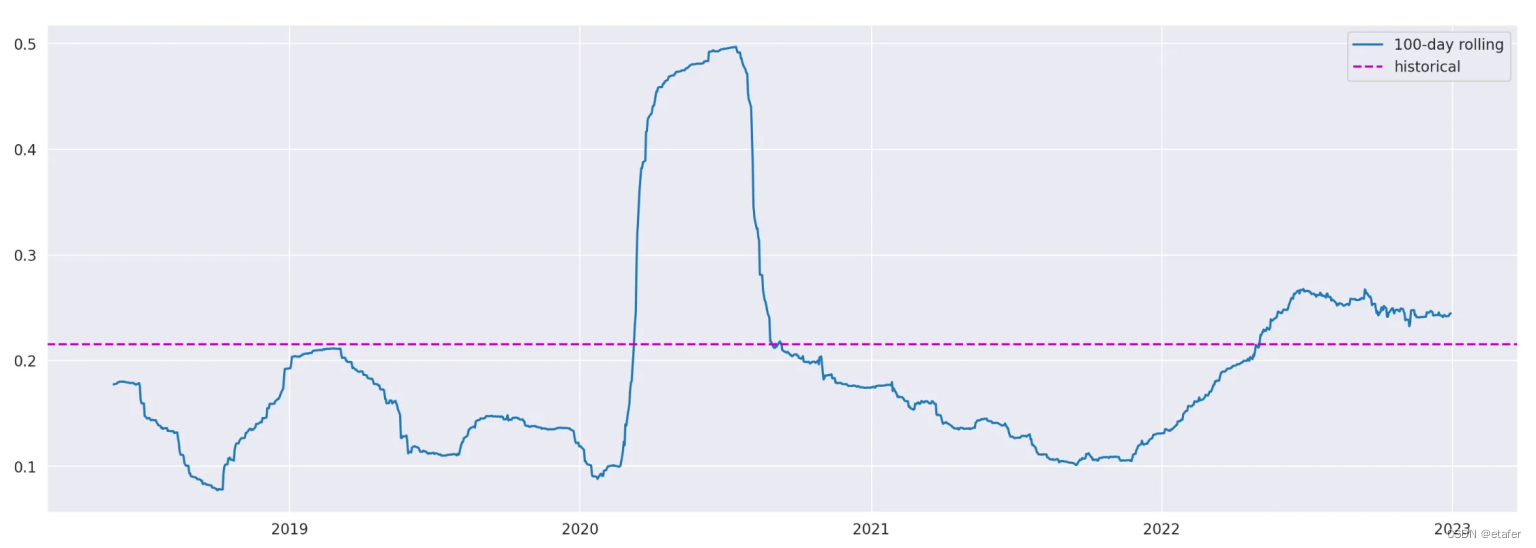
在这里插入图片描述

SPY波动性图

在这里插入图片描述

SPY历史波动性

我们可以在上面的图表中看到，使用滚动窗口计算出的波动性估计值与使用所有数据计算出的历史波动性有很大的偏差。让我们来看一下滚动波动性的一些描述性统计。

在这里插入图片描述

滚动波动性摘要统计数据

滚动波动性从7.74%变化到49.69%，平均值为19.2%。但即使真实波动性是恒定的，也预期会有一些滚动波动性的偏差。为了看看预期的偏差是什么样的，让我们生成一个具有与SPY回报相同均值和方差的正态分布回报的随机样本。然后我们可以通过将两者的滚动波动性放在一起对比。

np.random.seed(1)
rs = spy_ret.mean() + spy_ret.std() * np.random.randn(len(spy_ret))
rs = pd.Series(rs)
rs_rolling_std = rs.rolling(100).std().dropna() * np.sqrt(252) # 年化滚动标准差

plt.figure(figsize=(18,6))
plt.plot(rs_rolling_std, label='RS 100-day rolling')
plt.plot(spy_rolling_std, label='SPY 100-day rolling')
plt.axhline(spy_hist_std, label='historical', color='m', linestyle='dashed')
plt.legend()

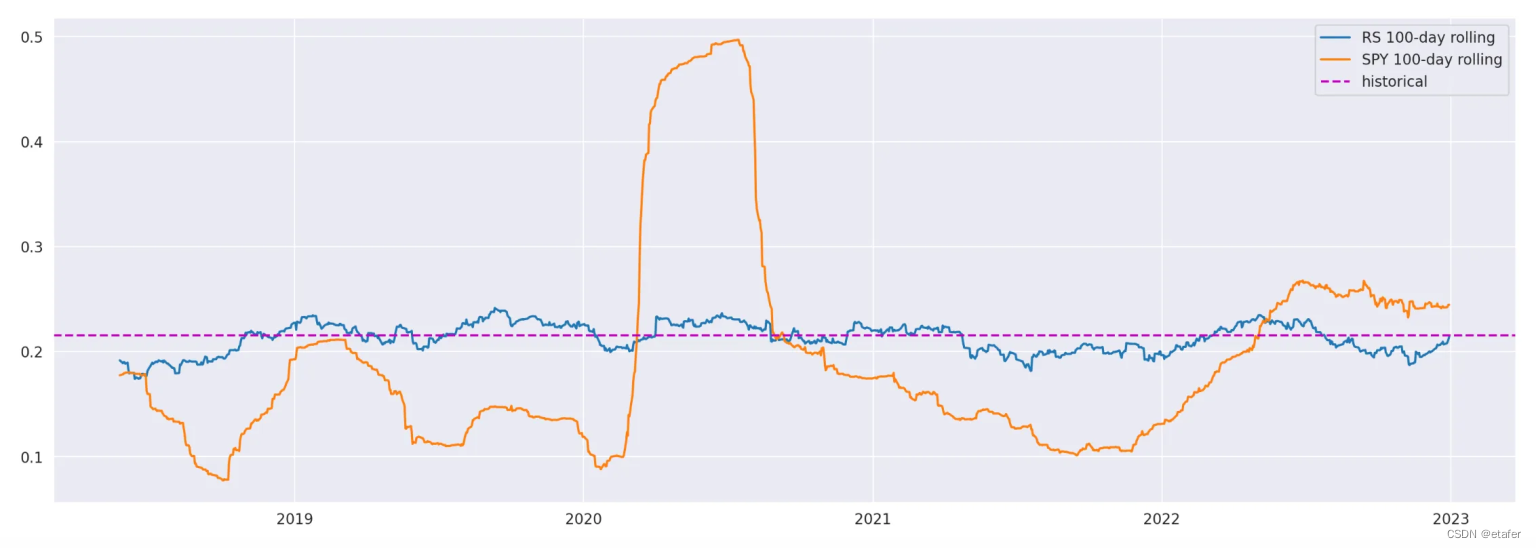
在这里插入图片描述

比较滚动波动性

正如您在上图中看到的，SPY的滚动波动性比随机样本的恒定波动性滚动波动性有更大的偏离历史波动性。下面我计算了两者滚动波动性的平均绝对偏差，并绘制了绝对偏差的直方图。

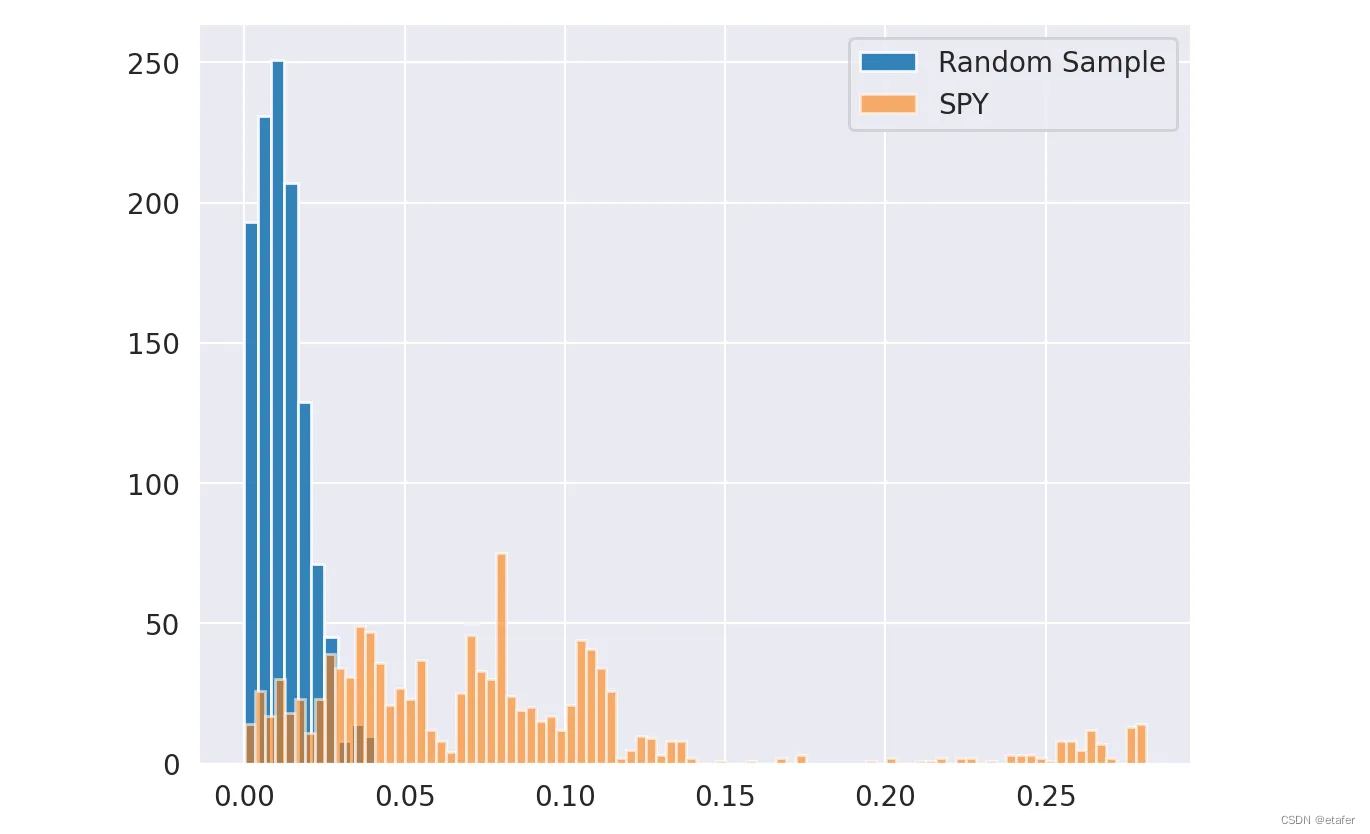
在这里插入图片描述

平均绝对偏差

在这里插入图片描述

绝对偏差的直方图

我们可以看到，SPY波动性的绝对偏差比随机样本的绝对偏差要大。但是我们上面所做的只涉及一个随机样本，我们实际上无法从中得出任何结论。为了解决这个问题，我们可以进行蒙特卡洛模拟。我们想回答以下问题：从具有恒定波动性的正态分布随机样本中获得如此大的滚动波动性偏差的概率是多少？

我们按照以下步骤进行：

  1. 进行10000次模拟。
  2. 在每次模拟中计算滚动波动性及其平均绝对偏差。
  3. 保存结果。
    下面展示了进行此操作的代码。
mean_std_diff = []

for i in range(10000):
    np.random.seed(i)
    rs = spy_ret.mean() + spy_ret.std() * np.random.randn(len(spy_ret))
    rs = pd.Series(rs)
    std_diff = rs.rolling(100).std().dropna() * np.sqrt(252) - spy_hist_std
    mean_std_diff.append(abs(std_diff).mean())

在这里插入图片描述

蒙特卡洛模拟结果

在10000个样本中，最大平均绝对偏差约为2.2%，这小于SPY的平均绝对偏差（7.9%）。我们可以得出结论，SPY滚动波动性来自于具有21.55%（SPY的历史波动性）恒定波动性的正态分布的概率小于0.0001。实际上，这个概率远远小于0.0001。我们可以使用结果的均值和标准差计算实际概率（p值），但知道它非常小已经足够我们使用了。

相关性

现在，让我们进行类似的关于相关性的研究。为此，我们需要另一种资产。我将使用代表黄金市场的GLD ETF。首先，我们下载数据并估计历史相关系数。

在这里插入图片描述

估计历史相关性

SPY和GLD之间的历史相关系数大约是0.1055。基本上这意味着两种资产之间几乎没有相关性。现在，让我们计算并绘制100天滚动相关性。

rolling_corr = spy_ret.rolling(100).corr(gld_ret).dropna()

plt.figure(figsize=(18,6))
plt.plot(rolling_corr, label='100-day rolling')
plt.axhline(hist_corr, label='historical', color='m', linestyle='dashed')
plt.legend()

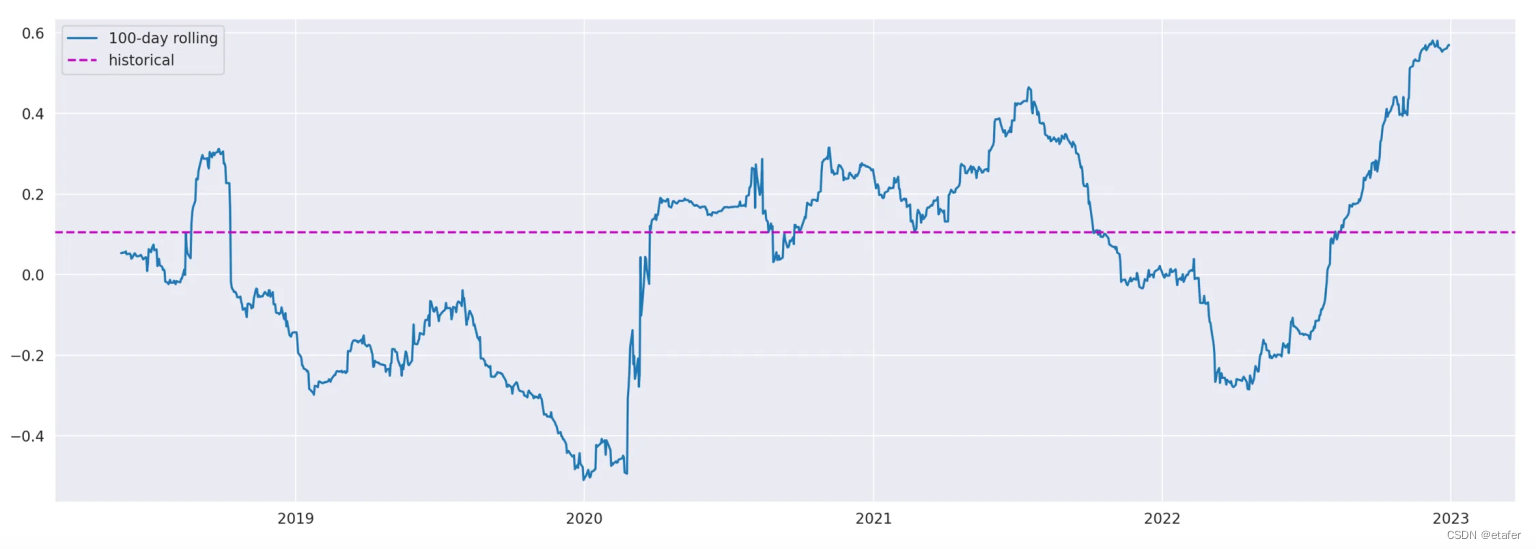
在这里插入图片描述

SPY-GLD相关系数图

在上面的截图中，我们可以看到滚动相关性与历史相关性有很大的偏差。它的范围从大约-0.5到+0.5，我们可以看到存在正相关、负相关或无相关的时期。当然，这将对最优投资组合产生巨大影响。让我们像对波动性那样，用一个随机样本的滚动相关性与这个结果进行比较。

我将生成一个具有SPY和GLD回报的均值和协方差矩阵的多元正态随机样本。然后，我会将该随机样本的滚动相关性添加到上面的图表中。

np.random.seed(1)
mu = np.array([spy_ret.mean(), gld_ret.mean()])
cov = np.cov(spy_ret, gld_ret)
rs = np.random.multivariate_normal(mean=mu, cov=cov, size=len(spy_ret))
rs = pd.DataFrame(rs, index=spy_ret.index)
rs_rolling_corr = rs[0].rolling(100).corr(rs[1]).dropna()

plt.figure(figsize=(18,6))
plt.plot(rolling_corr, label='SPY-GLD 100-day rolling')
plt.plot(rs_rolling_corr, label='RS 100-day rolling')
plt.axhline(hist_corr, label='historical', color='m', linestyle='dashed')
plt.legend()

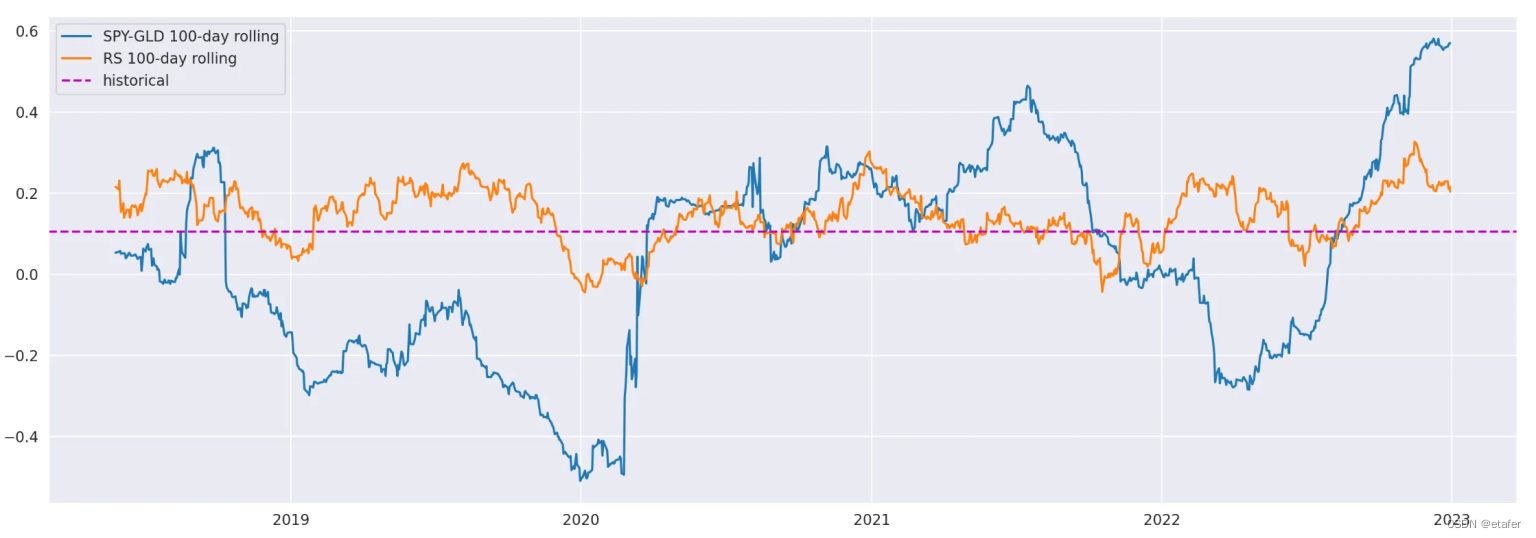
在这里插入图片描述

滚动相关性的比较

在这里插入图片描述

相关系数的平均绝对偏差

我们再次看到，SPY-GLD的滚动相关性与历史相关性相比，偏差显著超过随机样本的滚动相关性。SPY-GLD的平均绝对偏差为0.212，而随机样本的平均绝对偏差为0.067。
现在，让我们进行蒙特卡洛模拟，以估计获得类似SPY-GLD偏差的可能性。我生成了10000个随机样本，计算其100天滚动相关性及其与历史值的平均绝对偏差。

mean_corr_diff = []

mu = np.array([spy_ret.mean(), gld_ret.mean()])
cov = np.cov(spy_ret, gld_ret)

for _ in range(10000):
    rs = np.random.multivariate_normal(mean=mu, cov=cov, size=len(spy_ret))
    rs = pd.DataFrame(rs, index=spy_ret.index)
    rs_rolling_corr = rs[0].rolling(100).corr(rs[1]).dropna()
    corr_diff = rs_rolling_corr - hist_corr
    mean_corr_diff.append(abs(corr_diff).mean())

在这里插入图片描述

蒙特卡洛模拟结果

在10000个样本中平均绝对偏差的最大值是0.135，小于SPY-GLD的平均绝对偏差（0.212）。这意味着SPY和GLD的回报是正态分布且具有0.1055恒定相关性的概率小于0.0001。

厚尾效应

论文中的另一个测试用于显示金融数据具有“厚尾”特性。这是通过计算超过长期均值两个标准差的数据点的百分比来证明的。如果该值超过4.6%，则分布具有“厚尾”。这个数字来自正态分布，其中4.6%的回报超出均值的2个标准差（SD）。

让我们对两种资产的回报（SPY和GLD）进行这个测试。

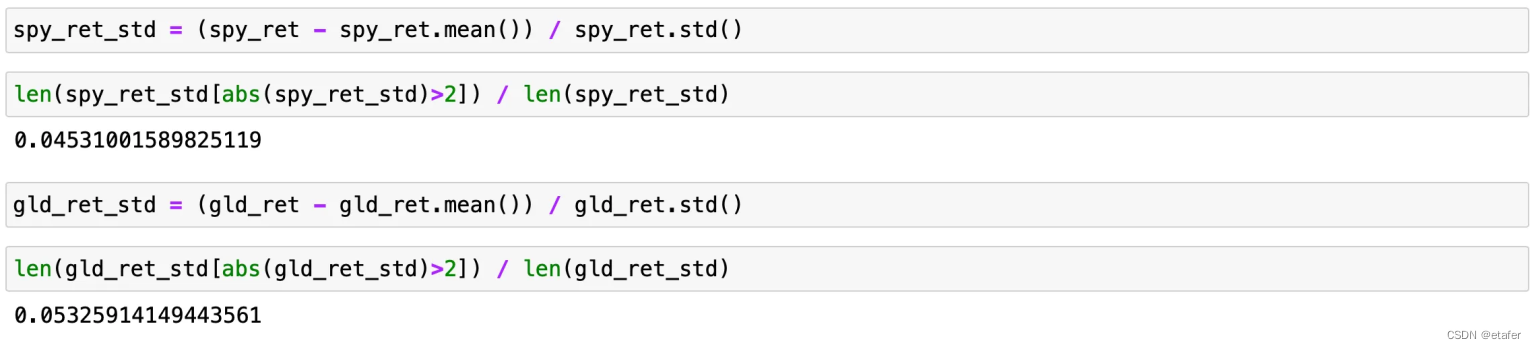
在这里插入图片描述

检测厚尾特性

在上面的截图中，我们可以看到大约4.53%的SPY回报超出均值的2个SD。这小于所需的4.6%，因此我们得出结论，SPY回报的分布没有“厚尾”。对于GLD，我们有5.32%的回报位于分布的尾部，因此GLD具有“厚尾”。

加权估计器

到目前为止，我们已经得出结论，回报的方差和相关系数不稳定并随时间变化。在这种情况下，我们应该如何估计它们呢？一种方法是只使用滚动窗口，每次估计仅包含最后N个数据点。我在上一篇文章中使用了这种方法。在论文中，作者提议使用加权估计器，这种估计器对较新的数据点给予更多的权重，而对较老的数据点给予较少的权重。上述公式就是用于计算加权协方差的方法。论文中的公式有一点不同 — 它不包含回报的期望值，因为假设它们为零。

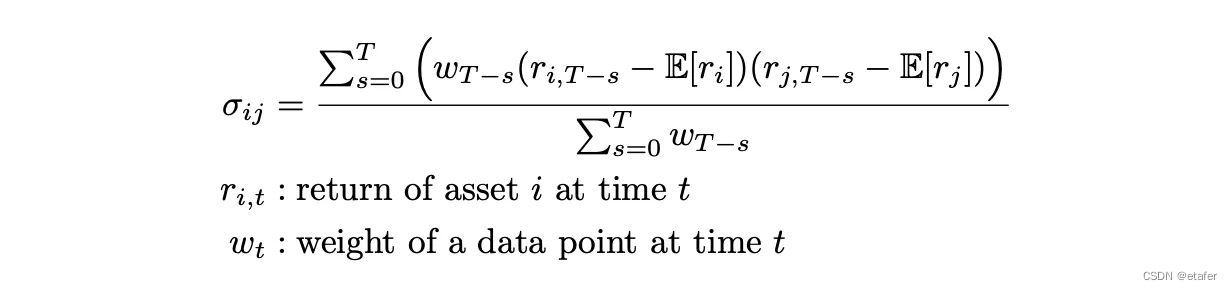
在这里插入图片描述

加权协方差计算公式

这个公式展示了如何根据每个数据点的时间序列权重来计算两个资产回报之间的加权协方差。每个回报值都减去了它的期望值（或均值），这样可以得到偏离均值的量，然后将资产i的偏离量与资产j的偏离量相乘。这个乘积会根据时间的远近被相应的权重加权。所有这些加权乘积的总和然后除以所有权重的总和，给出了加权协方差。如果回报的期望值假设为零，那么公式中的期望值（E[rᵢ]和E[rⱼ]）就会被省略。加权协方差是评估资产之间关系随时间变化和进行资产配置时的一种有用工具。

我同样会使用加权平均回报公式，如下图所示：
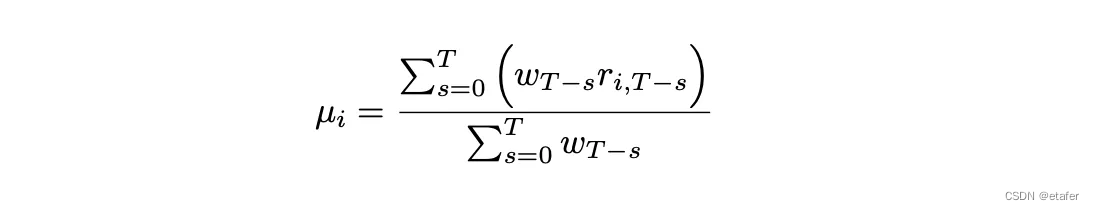
在这里插入图片描述

加权平均回报公式

这个公式用于计算资产回报的加权平均值。对于每个时间点的回报，都乘以一个权重，这个权重通常是根据数据点的新旧来分配的，新的数据点权重大，旧的数据点权重小。然后，这些加权回报的总和被所有权重的总和除，得到加权平均回报。使用加权平均的目的是让最近的观测结果对平均值有更大的影响，这在处理具有时变特征的金融数据时是有益的，因为最近的数据更能反映当前的市场状况。

如果我们想对较近期的观察结果给予更多的权重，wₜ 应该是时间的递减函数。在论文中，提出了上述函数。

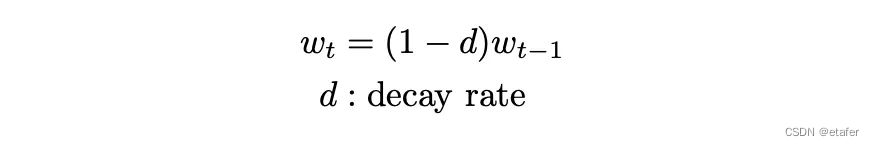
在这里插入图片描述

权重函数

例如，如果 d=0.1，则每一天的权重是后一天的90%。

让我们尝试比较使用加权估计器和滚动窗口估计器计算的结果。在下面的代码中，我使用两种方法计算了SPY和GLD之间的相关性。我使用了0.023的衰减率和252天的滚动窗口。计算加权协方差矩阵的函数已在numpy中实现。我们只需要提供一个权重向量作为输入变量。

d = 0.023 # 衰减率

weighted_corr = pd.Series(index=spy_ret.iloc[252:].index)

for t in spy_ret.iloc[252:].index:
    # 准备数据
    spy_tmp = spy_ret.loc[:t]
    gld_tmp = gld_ret.loc[:t]
    
    # 构建权重
    weights = [1]
    for _ in range(len(spy_tmp)-1):
        w = weights[-1] * (1-d)
        weights.append(w)
        
    # 计算加权协方差
    weighted_cov = np.cov(spy_tmp, gld_tmp, aweights=weights[::-1])
    
    # 将协方差转换为相关性
    D = np.sqrt(np.diag(np.diag(weighted_cov)))
    corr = (np.linalg.inv(D) @ weighted_cov @ np.linalg.inv(D))
    weighted_corr.loc[t] = corr[0,1]

plt.figure(figsize=(18,6))
plt.plot(spy_ret.rolling(252).corr(gld_ret), label='252-day rolling')
plt.plot(weighted_corr, label=f'weighted (d={d})')
plt.axhline(hist_corr, label='historical', color='m', linestyle='dashed')
plt.legend()

此代码段展示了如何使用加权方法和滚动窗口方法来计算SPY和GLD之间的相关性。加权相关性的计算通过为每一个时间点分配一个根据时间递减的权重来完成，这样最近的观测结果在计算中的影响更大。随后，代码使用这些权重来计算加权协方差矩阵，并将其转换为相关系数。然后，该代码绘制了基于252天滚动窗口计算的相关性与基于加权方法计算的相关性的对比图。使用衰减率是为了在分析金融时间序列数据时，能够更好地捕捉最近数据点的影响力，这通常认为能更准确地反映最新市场状况。通过对比不同方法得到的相关性，可以对资产之间关系的动态变化有更全面的了解。

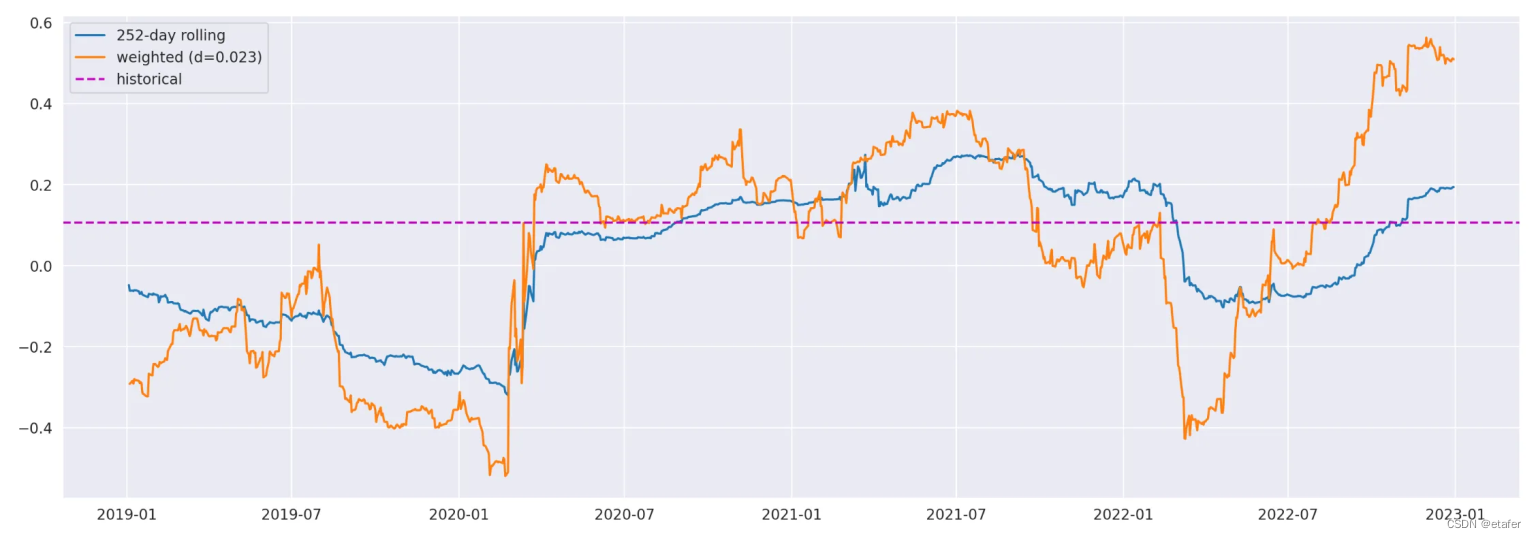
在这里插入图片描述

加权与滚动窗口相关性

在上图中，您可以同时看到两种相关性。252天滚动相关性看起来更平滑，并且不像加权相关性那样快速地对变化作出反应。我们可以通过调整衰减率来调节这种行为。我们应该基于我们的投资视角来选择它。随着衰减率的降低，我们的投资视角增加。在下面的屏幕截图中，您可以看到论文中显示德国10年期债券衰减率的表格。
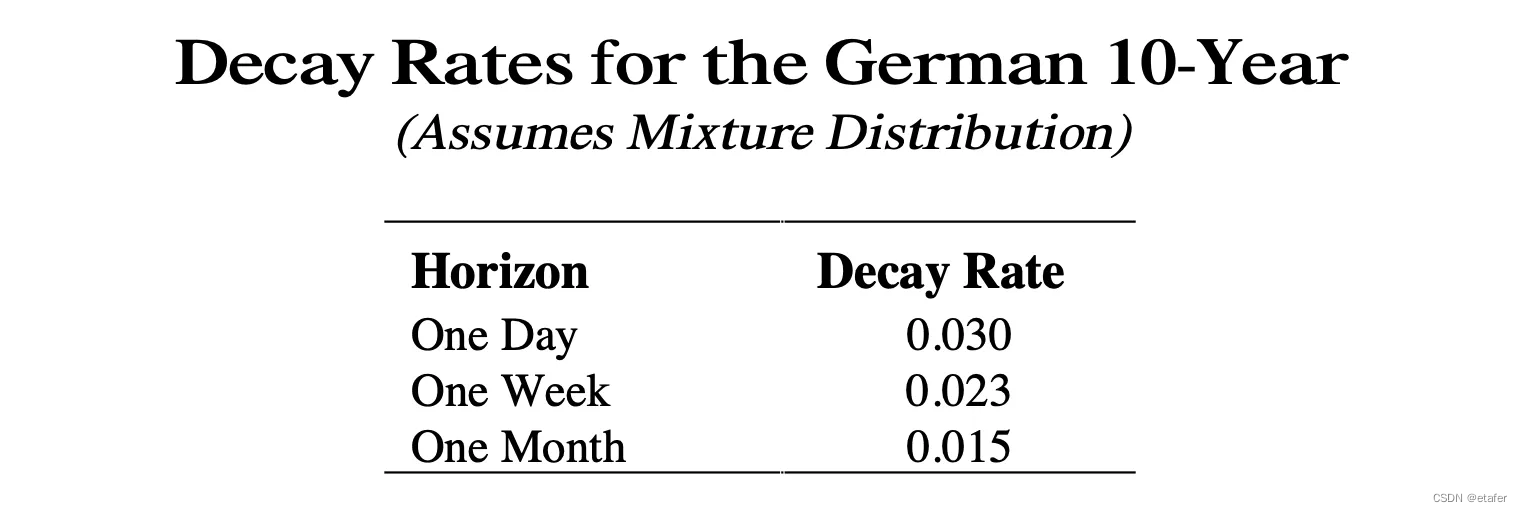
在这里插入图片描述

不同投资视角的衰减率

在论文中，作者提出了一种估计衰减率的方法，但这超出了本文的范围。有兴趣的读者可以参考论文的附录B。我只是打算使用0.023的衰减率（上表中一周投资视角的衰减率）。

交易策略表现：加权估计器与简单估计器的比较

现在让我们比较使用不同估计器的交易策略的表现。我们预期使用加权估计器的策略将比使用简单估计器的策略表现更好。我将使用以下代表不同资产类型的ETFs：

  • SPY —— 大盘股。
  • VWO —— 小盘股。
  • BNDX —— 债券。
  • USO —— 石油。
  • GLD —— 黄金。

投资组合将每周重新平衡。均值和协方差矩阵将使用日常数据估计。（使用更高频率的数据是另一种提高协方差估计精度的方法。）

stocks = ['SPY', 'VWO', 'BNDX', 'USO', 'GLD']

tmpdf = yf.download(stocks[0], start='2018-01-01', end='2022-12-31')
prices = pd.DataFrame(index=tmpdf.index, columns=stocks)
prices[stocks[0]] = tmpdf['Adj Close']
for stock in stocks[1:]:
    tmpdf = yf.download(stock, start='2018-01-01', end='2022-12-31')
    prices[stock] = tmpdf['Adj Close']

returns = prices.pct_change().dropna()

# 周价格和回报
prices_w = prices.resample('1W').last()
returns_w = prices_w.pct_change().dropna()

现在让我们看看历史相关性矩阵。
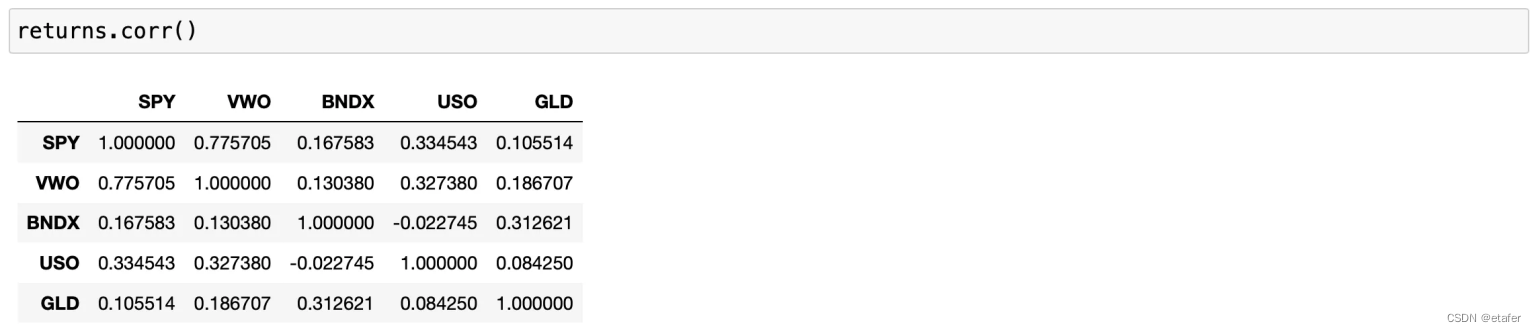
在这里插入图片描述

历史相关性矩阵

代表股票市场的ETFs（SPY和VWO）高度相关，相关系数为0.77。其他资产与股票市场以及彼此之间的相关性相对较低，这对基于MPT的投资组合优化是一个良好的特性。

等权重投资组合表现指标

现在我们准备实施我们的策略。首先让我们看一下等权重投资组合的表现指标。

cumret_eqw = (1 + returns_w.loc['2019-01-01':].sum(axis=1)/returns_w.shape[1]).cumprod()
results_df = pd.DataFrame(columns=['Total return', 'APR', 'Sharpe', 'Max DD', 'Max DD Duration'])
results_df.loc['Equally Weighted'] = calculate_metrics(cumret_eqw)

在这里插入图片描述

表现指标

接下来，我们将测试其他策略并查看它们是否提供更好的表现。

回想一下，当我们使用现代投资组合理论（MPT）解决投资组合优化问题时，我们有两个选择：要么最小化投资组合的波动性，要么在给定波动性水平的情况下最大化投资组合回报。为了进行公平比较，我将使用等权重投资组合的波动性作为我的目标波动性。它显示在下面的屏幕截图中。
在这里插入图片描述

等权重投资组合的波动性

MPT策略表现指标

现在我们将实施我们的第一种策略。在这里，我将使用252天滚动窗口来估计回报的均值和协方差。这与我在关于MPT的上一篇文章中使用的策略相同。下面展示了对其进行回测的代码。

def negative_annual_return(weights, returns):
    ret = weights.T @ returns.mean() * 252
    return -ret

def volatility(weights, returns):
    return np.sqrt(weights.T @ returns.cov() @ weights * 252)

positions = pd.DataFrame(index=prices_w.loc['2019-01-01':].index, 
                         columns=prices_w.columns)

target_vol = volatility_eqw
constraints = ({'type':'eq', 'fun': lambda x: volatility(x,returns_tmp)-target_vol}, 
               {'type':'eq', 'fun': lambda x: np.sum(x)-1})
bounds=[[0,1]]*len(stocks)
x0 = np.ones(len(stocks)) / len(stocks)

for t in tqdm(returns_w.loc['2019-01-01':].index):
    # 准备数据
    prices_tmp = prices.loc[:t].iloc[-252:]
    returns_tmp = prices_tmp.pct_change().dropna()
    
    # 优化过程
    res = minimize(negative_annual_return, x0, args=(returns_tmp), 
               bounds=bounds, constraints=constraints)
    if res.status!=0:
        print('Optimization failed')
        positions.loc[t] = positions.loc[:t].iloc[-2] # keep previous weights
    else:
        positions.loc[t] = res.x

cumret_rolling = (1 + (positions.shift() * returns_w.loc['2019-01-01':]).sum(axis=1)).cumprod()
results_df.loc['MPT (rolling window)'] = calculate_metrics(cumret_rolling)

在这里插入图片描述

表现指标

在这里插入图片描述

收益波动性

您可以看到，与等权重投资组合相比，这种策略的表现明显更差，其波动性高于目标波动性15.8%。

–

MPT策略使用加权估计器

接下来，我们将回测相同的策略，但是采用加权估计器。为此，我们需要实现新的函数来计算波动性和负回报，这些函数将用于均值-方差优化。这些函数与之前使用的类似，只不过采用了加权估计器。注意，我还使用加权均值来计算平均回报。其他一切保持不变。

# 1.定义加权波动性和年化负回报的函数
# 定义加权波动性的函数
def volatility_weighted(weights, returns, d):
    
    # 构造计算协方差矩阵的权重向量
    w = [1]
    for i in range(len(returns)-1):
        w.append(w[-1]*(1-d))
    
    # 计算加权协方差
    weighted_cov = np.cov(returns.T, aweights=w[::-1])
    
    # 返回年化波动性
    return np.sqrt(weights.T @ weighted_cov @ weights * 252)

# 定义年化负回报的函数
def negative_annual_return_weighted(weights, returns, d):
    
    # 构造计算加权平均的权重向量
    w = [1]
    for i in range(len(returns)-1):
        w.append(w[-1]*(1-d))
        
    # 计算加权平均
    weighted_mean = np.average(returns.T, weights=w[::-1], axis=1)
    
    # 返回年化回报的负值
    ret = weights.T @ weighted_mean * 252
    return -ret
# 2.实施投资组合优化并回测策略
# 初始化持仓DataFrame
positions = pd.DataFrame(index=prices_w.loc['2019-01-01':].index, 
                         columns=prices_w.columns)

# 设定目标波动性为等权重投资组合的波动性
target_vol = volatility_eqw
# 设定衰减率
d = 0.023
# 设定优化约束条件
constraints = ({'type':'eq', 'fun': lambda x: volatility_weighted(x,returns_tmp,d)-target_vol}, 
               {'type':'eq', 'fun': lambda x: np.sum(x)-1})
# 设定权重的界限
bounds=[[0,1]]*len(stocks)
# 初始权重
x0 = np.ones(len(stocks)) / len(stocks)

# 对每个周的回报进行循环优化
for t in tqdm(returns_w.loc['2019-01-01':].index):
    # 准备数据
    prices_tmp = prices.loc[:t]
    returns_tmp = prices_tmp.pct_change().dropna()
    
    # 使用scipy的minimize函数来执行优化
    res = minimize(negative_annual_return_weighted, x0, args=(returns_tmp, d), 
               bounds=bounds, constraints=constraints)
    
    # 检查优化是否成功
    if res.status!=0:
        print('Optimization failed')
        # 如果失败，保持上一次的权重
        positions.loc[t] = positions.loc[:t].iloc[-2]
    else:
        # 如果成功，更新权重
        positions.loc[t] = res.x

# 计算累积回报
cumret_weighted = (1 + (positions.shift() * returns_w.loc['2019-01-01':]).sum(axis=1)).cumprod()
# 将结果存入一个结果DataFrame中
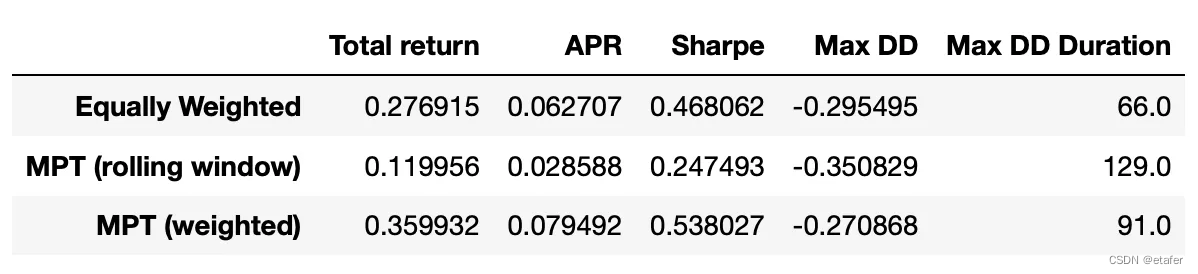
results_df.loc['MPT (weighted)'] = calculate_metrics(cumret_weighted)

在这里插入图片描述

表现指标

在这里插入图片描述

收益波动性

使用夏普比率优化投资组合

在之前的文章中，我提到过我们可以通过增加更多的约束或改变目标函数，根据我们的需求轻松修改投资组合优化问题。这里，我想展示一个这样的例子。

在上述策略中，我们使用了等权重投资组合的波动性作为目标波动性。我们试图最大化这一波动性水平的回报。但如果我们对投资组合的波动性没有严格限制呢？如果我们愿意为了更高的回报接受更多的风险呢？在这种情况下，我们可以修改投资组合优化问题，尝试最大化投资组合的夏普比率（它衡量风险调整后的回报）。

为此，我们需要实现一个计算负夏普比率的函数（我们将最小化这个函数）。函数的代码如下所示。目前，我正使用简单的均值和协方差估计器。

def negative_sharpe(weights, returns):
    ret = weights.T @ returns.mean() # 计算平均每日回报
    std = np.sqrt(weights.T @ returns.cov() @ weights) # 计算每日标准差
    sharpe = np.sqrt(252) * ret / std
    return -sharpe

现在我们准备进行回测。策略基本上和之前一样，我们只是改变了目标函数，并移除了波动性的约束。

positions = pd.DataFrame(index=prices_w.loc['2019-01-01':].index, 
                         columns=prices_w.columns)

constraints = ({'type':'eq', 'fun': lambda x: np.sum(x)-1})
bounds=[[0,1]]*len(stocks)
x0 = np.ones(len(stocks)) / len(stocks)

for t in tqdm(returns_w.loc['2019-01-01':].index):
    # prepare data
    prices_tmp = prices.loc[:t].iloc[-252:]
    returns_tmp = prices_tmp.pct_change().dropna()
    
    # perform optimization
    res = minimize(negative_sharpe, x0, args=(returns_tmp), 
               bounds=bounds, constraints=constraints)
    if res.status!=0:
        print('Optimization failed')
        positions.loc[t] = positions.loc[:t].iloc[-2] # keep previous weights
    else:   
        positions.loc[t] = res.x

cumret_sharpe = (1 + (positions.shift() * returns_w.loc['2019-01-01':]).sum(axis=1)).cumprod()

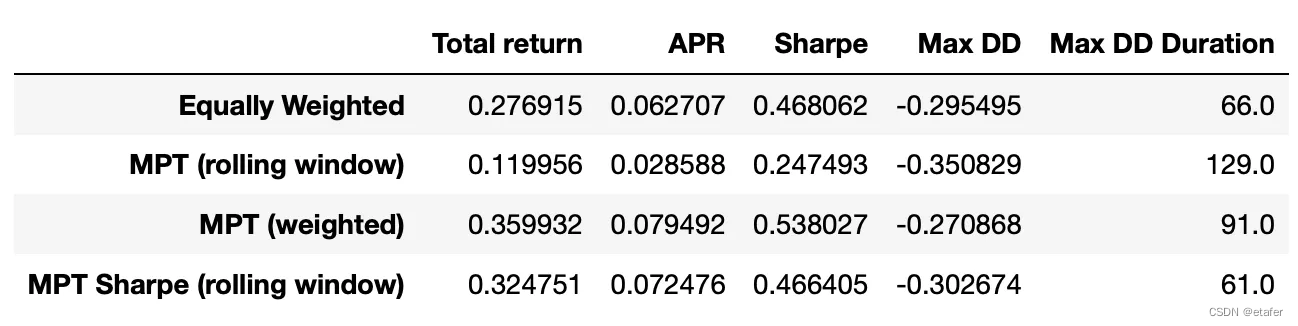
在这里插入图片描述

表现指标

即使使用滚动窗口技术，这种方法也能让我们取得更好的表现（与经典的使用滚动窗口的MPT相比）。如果我们使用加权估计器会怎样呢？为此，我们需要实现一个使用加权均值和协方差估计器计算夏普比率的函数。代码如下。

def negative_sharpe_weighted(weights, returns, d):
    
    # 为加权估计构造权重向量
    w = [1]
    for i in range(len(returns)-1):
        w.append(w[-1]*(1-d))
    
    # 计算加权投资组合回报
    weighted_mean = np.average(returns.T, weights=w[::-1], axis=1)
    ret = weights.T @ weighted_mean
    
    # 计算加权投资组合的标准差
    weighted_cov = np.cov(returns.T, aweights=w[::-1])
    std = np.sqrt(weights.T @ weighted_cov @ weights)
    
    # 计算夏普比率
    sharpe = np.sqrt(252) * ret / std
    
    return -sharpe

现在我们准备进行回测。再次，一切都相同，我们只需要改变我们正在最小化的目标函数。

positions = pd.DataFrame(index=prices_w.loc['2019-01-01':].index, 
                         columns=prices_w.columns)

constraints = ({'type':'eq', 'fun': lambda x: np.sum(x)-1})
bounds=[[0,1]]*len(stocks)
x0 = np.ones(len(stocks)) / len(stocks)
d = 0.023

for t in tqdm(returns_w.loc['2019-01-01':].index):
    # 准备数据
    prices_tmp = prices.loc[:t]
    returns_tmp = prices_tmp.pct_change().dropna()
    
    # 执行优化
    res = minimize(negative_sharpe_weighted, x0, args=(returns_tmp, d), 
               bounds=bounds, constraints=constraints)
    if res.status!=0:
        print('Optimization failed')
        positions.loc[t] = positions.loc[:t].iloc[-2] # 保持之前的权重
    else:    
        positions.loc[t] = res.x

cumret_sharpe_weighted = (1 + (positions.shift() * returns_w.loc['2019-01-01':]).sum(axis=1)).cumprod()
results_df.loc['MPT Sharpe (weighted)'] = calculate_metrics(cumret_sharpe_weighted)

表现指标显示在下面的表中。到目前为止，根据夏普比率和年化收益率，这个策略有最好的表现。它也有最短的最大回撤持续时间。

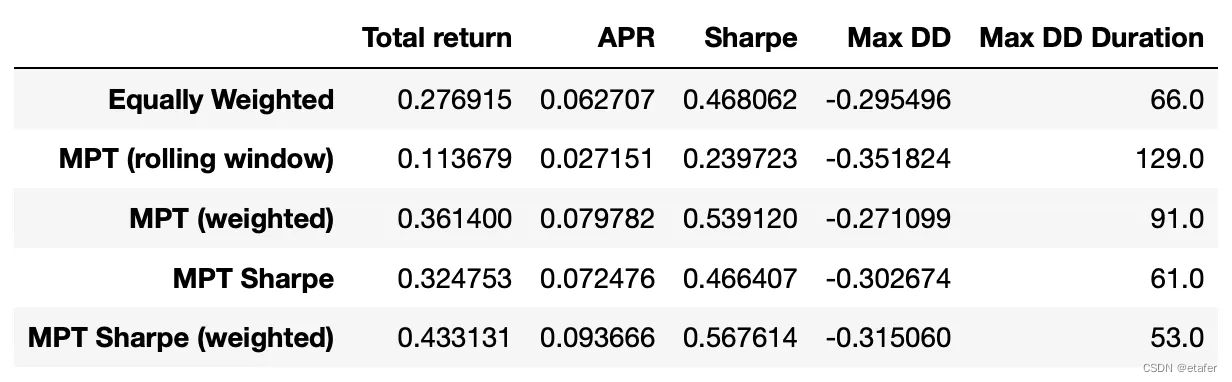
在这里插入图片描述

表现指标

回想一下，我没有实现任何估计衰减率的方法。我只是使用了论文中的一个值。我认为我们可以通过使用更好的衰减率值来进一步提高表现。最简单的方法可能是回测几个值，并选择表现最好的一个。另一种方法是使用似然函数估计衰减率（在论文的附录B中有描述）。

总结

我们已经看到，使用加权估计器可以在两种类型的交易策略中提高表现。请注意，在量化金融的许多其他领域（不仅仅是投资组合优化），改进协方差估计也很重要。例如，我们可以尝试在对冲交易策略中使用加权估计器，对冲交易策略使用相关系数进行对冲选择。

总之，尽管使用加权估计器允许我们改进最优投资组合的表现（与简单的滚动窗口估计器相比），但我们的策略的表现仍然相当低。在接下来的文章中，我将继续探索投资组合优化的主题，并尝试构建表现更好的交易策略。

源码jupyter notebook请点击此处。

etafer
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
蒙特卡罗方法在投资组合优化中的应用
AI架构设计之禅
07-24 292
投资组合是一个由若干个资产组成的集合，它们的价值都相加等于整个组合的价值。然后，定义股票市场的状况。这里，我们假定市场中的每只股票都有一个具有可变长期的期望回报的长期市场内的相互影响机制。也就是说，任何一个股票都是由其他股票所影响的，而这些股票又由各种因素所引起。
投资组合：利用随机矩阵理论估计协方差矩阵的投资组合优化
etafer的博客
04-25 170
本文探讨了如何使用随机矩阵理论（RMT）来优化投资组合的协方差矩阵估计，从而提升投资组合的性能。首先使用生成数据验证了模型，确保均值和协方差矩阵的稳定性，然后将数据分为训练集和测试集以寻找最优投资组合并计算实际收益。文章详细说明了使用算术收益而非对数收益的原因，并描述了如何通过保留超出RMT界限的最大特征值信息来过滤相关矩阵。使用过滤后的协方差矩阵进行均值-方差优化，比起传统方法，在性能上有所提升，特别是在回测策略时速度更快。尽管测试结果与现有文献有所差异，这提示未来研究需要进一步探究并可能对模型进行改
加权协方差矩阵(weighted covariance matrix)
就很秃然
11-15 1456
国内完全没一个有用的，这里给出了加权协方差矩阵计算函数。用的时候可以将权重先归一化。
加权协方差矩阵：计算加权协方差矩阵-matlab开发
05-30
WEIGHTEDCOV 返回加权协方差的对称矩阵 C，该矩阵根据输入 T×N 矩阵 Y 计算，该矩阵 Y 的行是观察值，列是变量，以及输入 T×1 的观察值权重向量 w。 如果观察结果并非完全相同并且需要根据某些理论假设或知识进行加权，则此函数可能是 COV 的有效替代方案。 C = WEIGHTEDCOV(Y, w) 返回一个半正定矩阵 C，即它的所有特征值都是非负的。 如果 w =ones(size(Y, 1), 1)，WEIGHTEDCOV(Y, w) 和 COV(Y, 1) 之间没有区别。 参考：矩阵表示法中的数学公式可在 F. Pozzi、T. Di Matteo、T. Aste 的“指数平滑加权相关”中找到，欧洲物理杂志 B，第 85 卷，第 6 期，2012 年。DOI:10.1140/epjb/ e2012-20697-x。 例子： % 生成相关的随机过程T = 1
加权平均数以及方差
热门推荐
铭记_
01-23 5万+
加权平均值即将各数值乘以相应的权数，然后加总求和得到总体值，再除以总的单位数。平均数的大小不仅取决于总体中各单位的标志值（变量值）的大小，而且取决于各标志值出现的次数（频数），由于各标志值出现的次数对其在平均数中的影响起着权衡轻重的作用，因此叫做权数。 加权平均值 即将各数值乘以相应的权数，然后加总求和得到总体值，再除以总的单位数。 平均数的大小不仅取决于总体中各单位的标志值
基于协方差权重插值算法
羽凌寒
12-08 2179
简介 　　本篇主要记录下基于图像协方差计算插值权重的单帧图像细节保持插值算法。参考论文:New Edge-Directed Interpolation 基本原理 　　这里网上截取了一段协方差定义及计算方法： 1 Xi 1.1 1.9 3 2 Yi 5.0 10.4 14.6 3 E(X) = (1.1+1.9+3)/3=2
投资组合：投资组合优化和现代投资组合理论
etafer的博客
04-22 142
本文介绍了现代投资组合理论（MPT）的基本概念，其中包括使用历史数据来优化投资组合，以在特定的风险水平下最大化预期回报。通过Python演示了如何生成随机投资组合，计算它们的预期回报和波动性，并探讨了最小方差投资组合和给定风险水平下回报最大化的策略。文章还涉及了允许和禁止做空的情况下的有效边界绘制，并通过回测验证了策略性能。尽管使用了简单的历史均值和协方差矩阵估算器，策略表现出色，但估算误差可能导致最优投资组合性能下降，并计划在后续文章中探索不同的估算器对投资组合性能的影响。
论文研究 - 使用Markowitz均值方差方法对加纳证券交易所的某些股票进行投资组合优化
05-22
在加纳，建立具有标准化优化的投资组合仍然是一个神话，因此，本研究显示了Markowitz模型如何在加纳证券交易所应用，并揭示了精选股票中最有效的投资组合，以减轻投资者的负担。 该研究使用了2011年至2016年股票...
AlgoTradingSimulatedPaths:MATLAB中的均值方差投资组合优化和算法交易策略
04-05
shrinkage.m将lambda I添加到估计的协方差矩阵并应用二次优化pca_optimisation.m根据PCA因子构建协方差矩阵，并用于二次优化ledoit_wolf.m -Ledoit和Wolf的二次收缩估算器mean_correlation.m风险平价方法，使用相关...
matlab.zip_matlab股票_wind股票_均值-VaR_均值VaR_投资组合
07-14
实验名称:投资组合分析 实验性质：综合性和研究探索性 实验目的：熟练运用投资组合...选择一组股票作为投资标的，构造投资组合，通过估计收益率均值、计算方差、协方差，计算该投资组合权重、在险价值、画出有效前沿。
马科维茨投资组合：马科维茨投资组合优化-matlab开发
05-29
通过最小化加权协方差矩阵来发现最佳投资组合权重
PortOpt:使用Markowitz（1952）均值方差模型的投资组合优化器-开源
04-29
您必须提供PortOpt（在文本文件中，或者-如果使用api-使用您自己的代码），资产的方差/协方差矩阵，平均收益和代理商风险偏好。 它返回组成最佳投资组合的资产份额向量。 为了最大程度地减少方差，它在内部使用...
常微分方程算法之编程示例六-解一阶方程组（龙格-库塔法）
最新发布
欢迎各位大佬光临“寒舍”！请多多指点，共同进步！
06-27 295
主要对本专栏介绍的常微分方程差分格式进行算例补充。
算法常见问题
u012374012的专栏
06-24 931
是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机。线性可分SVM当训练数据线性可分时，通过最大化硬间隔（hard margin）可以学习得到一个线性分类器，即硬间隔SVM。线性SVM当训练数据不能线性可分但是近似线性可分时，通过最大化软间隔（soft margin）也可以学习到一个线性分类器，即软间隔SVM。非线性SVM当训练数据线性不可分时，通过使用核技巧（kernel trick）和最大化软间隔，可以学习到一个非线性SVM。
排序算法系列二：归并排序、快速排序
暗黑世界
06-22 443
一、概念 二、实现 三、时间空间复杂度 四、优缺点
560. 和为 K 的子数组
侯仕奇的博客
06-26 203
给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数。子数组是数组中元素的连续非空序列。整体时间复杂度优化为 O(n。
【算法】二叉树 - 理论基础
Nanki_的博客
06-23 1267
int val;
用matlab计算鲁棒均值-CVaR投资组合优化模型的程序
05-25
以下是用MATLAB计算鲁棒均值-CVaR投资组合优化模型的程序： ``` % 设置数据 n = 10; % 资产数量 mu = rand(n,1); % 平均收益率 Sigma = rand(n); % 协方差矩阵 w0 = ones(n,1)/n; % 初始权重 % 定义优化问题 cvx_...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值