投资组合：利用随机矩阵理论估计协方差矩阵的投资组合优化

投资组合：利用随机矩阵理论估计协方差矩阵的投资组合优化

github仓库地址：https://github.com/financialnoob/portfolio_optimization
原文链接：https://financialnoob.me/portfolio-optimization-random-matrix-approach-to-estimating-covariance-matrix/

---

系列文章

1. 投资组合优化核现代投资组合理论
2. 使用加权均值和协方差估计器的投资组合优化
3. 利用随机矩阵理论估计协方差矩阵的投资组合优化

---

---

前言

在投资组合优化中，估计协方差矩阵是一大挑战。样本协方差矩阵往往噪声很大，随着数据集中股票数量的增加，问题会显著恶化。本文将介绍并实现一种基于随机矩阵理论（RMT）的协方差矩阵估计方法，该方法源于论文《金融数据中的交叉相关性的随机矩阵方法》（Plerou 等，2001年）。

假设我们想要估计500只股票的协方差矩阵。为此，我们需要估计500499/2 = 124750个单独的协方差。包含500只股票一年日常价格的数据集约有500250=125000个数据点。这意味着我们每个参数（一对股票之间的协方差）略多于一个数据点。因此，样本协方差矩阵非常嘈杂，并包含许多随机成分。一种可能的解决方案是使用更多的数据——不是一年，而是二十年或三十年。但问题在于，协方差并不稳定，随时间变化（这在我之前的文章中已经展示过），因此旧数据并不真正有用。另一种方法是使用高频数据以获取更多数据点，但即使如此，我们能获得的数据量也是有限的。在该论文中，作者提出了一种基于随机矩阵理论的解决方案。与其使用协方差矩阵，不如关注相关矩阵，但相关性只是协方差的重新缩放形式，我们可以轻易地将一个转换为另一个。

主要思想很简单。我们可以比较样本相关矩阵的性质与由不相关时间序列构造的随机相关矩阵（此类矩阵称为Wishart矩阵）的性质。如果我们发现两个矩阵的性质有任何偏差，那么这些偏差将包含关于相关性的“真实”信息。然后我们可以将样本相关矩阵的内容分为两部分：

• 与随机相关矩阵的性质相匹配的部分——“噪声”。
• 与随机相关矩阵的性质偏离的部分——“信息”。

为了在实践中实施这一想法，我们将使用随机矩阵理论（RMT）。RMT最初是为分析复杂的量子系统（模拟重原子的核）而开发的。现在它在许多不同的领域中得到应用——数学统计、物理学、数论、神经科学等。在本文中，我们将尝试将其应用于金融数据。

---

特征值分析

我将使用截至写作时标普500指数成分股中的490只股票的价格数据，数据覆盖2018年1月1日至2022年12月31日的每日分辨率。以下展示了下载和准备数据的代码。

sp500 = 'MMM AOS ABT ABBV ACN ADM ADBE ADP AES AFL A ABNB APD AKAM ALK ALB ARE ALGN ALLE LNT ALL GOOGL GOOG MO AMZN AMCR AMD AEE AAL AEP AXP AIG AMT AWK AMP AME AMGN APH ADI ANSS AON APA AAPL AMAT APTV ACGL ANET AJG AIZ T ATO ADSK AZO AVB AVY AXON BKR BALL BAC BBWI BAX BDX WRB BRK-B BBY BIO TECH BIIB BLK BX BK BA BKNG BWA BXP BSX BMY AVGO BR BRO BF-B BG CHRW CDNS CZR CPT CPB COF CAH KMX CCL CARR CTLT CAT CBOE CBRE CDW CE COR CNC CNP CDAY CF CRL SCHW CHTR CVX CMG CB CHD CI CINF CTAS CSCO C CFG CLX CME CMS KO CTSH CL CMCSA CMA CAG COP ED STZ CEG COO CPRT GLW CTVA CSGP COST CTRA CCI CSX CMI CVS DHI DHR DRI DVA DE DAL XRAY DVN DXCM FANG DLR DFS DIS DG DLTR D DPZ DOV DOW DTE DUK DD EMN ETN EBAY ECL EIX EW EA ELV LLY EMR ENPH ETR EOG EPAM EQT EFX EQIX EQR ESS EL ETSY EG EVRG ES EXC EXPE EXPD EXR XOM FFIV FDS FICO FAST FRT FDX FITB FSLR FE FIS FI FLT FMC F FTNT FTV FOXA FOX BEN FCX GRMN IT GEHC GEN GNRC GD GE GIS GM GPC GILD GL GPN GS HAL HIG HAS HCA PEAK HSIC HSY HES HPE HLT HOLX HD HON HRL HST HWM HPQ HUBB HUM HBAN HII IBM IEX IDXX ITW ILMN INCY IR PODD INTC ICE IFF IP IPG INTU ISRG IVZ INVH IQV IRM JBHT JKHY J JNJ JCI JPM JNPR K KVUE KDP KEY KEYS KMB KIM KMI KLAC KHC KR LHX LH LRCX LW LVS LDOS LEN LIN LYV LKQ LMT L LOW LULU LYB MTB MRO MPC MKTX MAR MMC MLM MAS MA MTCH MKC MCD MCK MDT MRK META MET MTD MGM MCHP MU MSFT MAA MRNA MHK MOH TAP MDLZ MPWR MNST MCO MS MOS MSI MSCI NDAQ NTAP NFLX NEM NWSA NWS NEE NKE NI NDSN NSC NTRS NOC NCLH NRG NUE NVDA NVR NXPI ORLY OXY ODFL OMC ON OKE ORCL OTIS PCAR PKG PANW PARA PH PAYX PAYC PYPL PNR PEP PFE PCG PM PSX PNW PXD PNC POOL PPG PPL PFG PG PGR PLD PRU PEG PTC PSA PHM QRVO PWR QCOM DGX RL RJF RTX O REG REGN RF RSG RMD RVTY RHI ROK ROL ROP ROST RCL SPGI CRM SBAC SLB STX SEE SRE NOW SHW SPG SWKS SJM SNA SEDG SO LUV SWK SBUX STT STLD STE SYK SYF SNPS SYY TMUS TROW TTWO TPR TRGP TGT TEL TDY TFX TER TSLA TXN TXT TMO TJX TSCO TT TDG TRV TRMB TFC TYL TSN USB UDR ULTA UNP UAL UPS URI UNH UHS VLO VTR VLTO VRSN VRSK VZ VRTX VFC VTRS VICI V VMC WAB WBA WMT WBD WM WAT WEC WFC WELL WST WDC WRK WY WHR WMB WTW GWW WYNN XEL XYL YUM ZBRA ZBH ZION ZTS'
sp500 = sp500.split()
start = '2018-01-01'
end = '2022-12-31'
tmpdf = yf.download(sp500[0], start=start, end=end)
prices = pd.DataFrame(index=tmpdf.index, columns=sp500)
for stock in sp500:
    tmpdf = yf.download(stock, start=start, end=end)
    prices[stock] = tmpdf['Adj Close']
prices = prices.dropna(axis=1)
returns = prices.pct_change().dropna()

请注意，我使用简单（算术）收益而不是论文中使用的对数收益，稍后我将解释这样做的原因。我也不标准化收益。我们处理的是相关矩阵，标准化后相关矩阵不会改变。还请记住，我们总是处理相关矩阵。有时我可能会说“随机样本的特征值”，但我的真实意思是“随机样本的相关矩阵的特征值”。

准备好数据后，我们可以进行论文中的一些测试。让我们从分析相关矩阵的特征值开始。我假设读者熟悉特征值和特征向量的概念。这里的主要思想是比较收益相关矩阵的特征值分布与不相关随机变量的随机相关矩阵的特征值分布。因此，让我们生成一些不相关的随机样本并保存它们相关矩阵的特征值。下面展示了执行此操作的代码。我使用与真实收益相同的均值和方差，但将协方差矩阵的非对角线元素设置为零（使它们不相关）。

# 设置参数
mean = returns.mean()
cov = np.diag(returns.var()) # 对角线元素之外为0 => 没有相关性

evalues_rs = []

# 生成100个样本并保存相关矩阵的特征值
for _ in tqdm(range(100)):
    rs = np.random.multivariate_normal(mean=mean, cov=cov, size=len(returns))
    evls = np.linalg.eigh(np.corrcoef(rs.T))[0]
    evalues_rs.extend(list(evls))

根据随机矩阵理论，我们知道随机相关矩阵特征值的解析分布。其定义如下所示。

特征值的解析分布

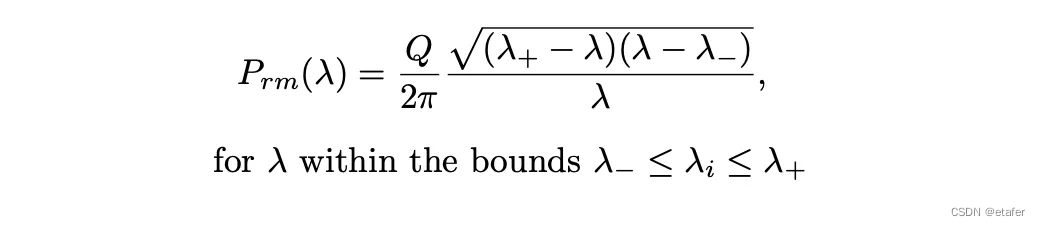
根据随机矩阵理论，我们知道随机相关矩阵特征值的解析分布。这个分布的公式如下所示：$P_{rm}(\lambda )=\frac{Q}{2\pi }\frac{\sqrt{({\lambda }_{+}-\lambda )(\lambda -{\lambda }_{-})}}{\lambda }$
其中，$(P_{rm}(\lambda ))$ 是在特定的界限 $({\lambda }_{-}\le {\lambda }_i\le {\lambda }_{+})$ 内，随机相关矩阵特征值的概率密度函数。这个分布帮助我们识别出哪些特征值反映了真实的、非随机的数据特性，而不仅仅是随机噪声。

计算 lambda 的界限如下所示。

计算 lambda的界限

现在，让我们比较我们随机样本的特征值分布与上面定义的解析分布。首先我们需要计算界限 ${\lambda }_{+}$ 和 ${\lambda }_{-}$。

计算 lambda+ 和 lambda-

现在我们可以计算解析分布，并将其与随机样本的分布一起绘制出来。

```python
# 概率分布
ls = np.linspace(lambda_minus, lambda_plus)
P_rm = [Q / (2*np.pi) * np.sqrt((lambda_plus - x) * (x - lambda_minus)) / x for x in ls]

# 与解析分布对比的不相关随机样本的特征值
plt.figure(figsize=(18,6))
plt.hist(evalues_rs, density=True, bins=50, alpha=0.8, label='随机样本')
plt.plot(ls, P_rm, color='m', linewidth=4, linestyle='dashed', label='解析分布')
plt.legend()
plt.xlabel('特征值')
plt.ylabel('频率')

随机样本特征值与解析分布的对比

如上图所示，我们得到了几乎完美的匹配。

现在我们将使用实际收益数据重复同样的过程。由于随机样本和实际收益的维度相等，$\lambda$的界限保持不变。有一点不同，现在我将创建两个图表 —— 一个用于小于等于3的特征值，另一个用于大于3的特征值。

# 实际相关矩阵的特征值
corr = returns.corr()
evalues = np.linalg.eigh(corr)[0]

# 实际收益的特征值与解析分布对比（特征值<=3）
plt.figure(figsize=(18,6))
plt.hist(evalues[evalues<=3], density=True, bins=50, label='实际收益')
plt.plot(ls, P_rm, color='m', linewidth=4, linestyle='dashed', label='解析分布')
plt.legend()
plt.xlabel('特征值')
plt.ylabel('频率')

# 实际收益的特征值与解析分布对比（特征值>3）
plt.figure(figsize=(18,6))
plt.hist(evalues[evalues>3], density=True, bins=50, label='实际收益')
plt.ylim(0,1.0)
plt.legend()
plt.xlabel('特征值')
plt.ylabel('频率')

实际收益特征值与解析分布对比（特征值≤3）

实际收益特征值与解析分布对比（特征值>3）

我们还可以计算偏离的特征值数量。

偏离的特征值数量

如上所述，超过一半的特征值（490−15−173=302）在随机矩阵理论的界限内。我们最感兴趣的是最大的特征值。在论文中，2%的特征值大于上界 ${\lambda }_{+}$。我们有15/490≈3% 的特征值大于 ${\lambda }_{+}$。

---

特征向量分量分析

接下来我将检查特征向量分量的分布。下图显示了三个最大特征值对应的三个特征向量的分量直方图（上排），以及位于随机矩阵理论界限内的特征值对应的三个特征向量的分量直方图（下排）。根据随机矩阵理论，随机相关矩阵的特征向量分量在重新缩放后应呈正态分布。这个分析分布用橙色显示。

evalues,evectors = np.linalg.eigh(returns.corr())

comps = [-1,-2,-3,-50,-150,-250] # 要绘制的特征向量的索引

fig, axs = plt.subplots(2,3, figsize=(18,8))

for ax,i in zip(axs.flatten(),comps):
    components = evectors[:,i] / np.sqrt(1/len(evalues))
    ls = np.linspace(-3,3)
    ax.hist(components, density=True, bins=30, label='特征向量分量')
    ax.plot(ls, 1/np.sqrt(2*np.pi) * np.exp(-ls**2/2), linewidth=3, label='分析分布')
    ax.set_ylim(0,0.8)
    ax.set_title(f'特征向量 {-i}')
    ax.legend()

特征向量分量的分布

顶部特征向量的分量明显不同于正态分布。底部行的分量（对应于随机矩阵理论界限内的特征值）更接近它们的分析（正态）分布。

下图为位于随机矩阵理论界限内的所有特征向量的分量分布。尽管它不是严格的正态分布（我们在零附近有更多分量），但它非常接近。

# 从 lambda- 到 lambda+ 的所有分量
comp_rmt_ind = np.where((evalues>lambda_minus) & (evalues<lambda_plus))
comp_rmt = evectors[:,comp_rmt_ind].flatten() / np.sqrt(1/len(evalues))
ls = np.linspace(-4,4)
plt.figure(figsize=(18,6))
plt.hist(comp_rmt, density=True, bins=100, label='特征向量分量')
plt.plot(ls, 1/np.sqrt(2*np.pi) * np.exp(-ls**2/2), linewidth=3, label='分析分布')
plt.xlim(-4,4)
plt.legend()

随机矩阵理论界限内所有分量的分布

---

特征组合与市场表现对比

在下一个测试中，我们对最大特征值及其对应特征向量进行解释。作者在第六节 B 部分声称，它代表了市场的影响，这是所有股票共有的。为了证实这一点，我们使用（标准化的）特征向量分量作为权重来创建一个股票组合。然后我们将该特征组合的收益与市场的收益（由 SPY ETF 代表）进行比较。作为对比，我还计算了对应于随机矩阵理论界限内特征值的组合的收益。

spy = yf.download('SPY', start='2018-01-01', end='2023-01-01')['Adj Close']
spy = spy.pct_change().dropna() # SPY 收益

epf1 = (evectors[:,-1]/evectors[:,-1].sum() * returns).sum(axis=1) # 特征组合1的收益
epf1.index = pd.to_datetime(epf1.index) 
epf100 = (evectors[:,-100]/evectors[:,-100].sum() * returns).sum(axis=1) # 特征组合100的收益
epf100.index = pd.to_datetime(epf100.index) 

# 标准化收益
spy_std = (spy - spy.mean()) / spy.std()
epf1_std = (epf1 - epf1.mean()) / epf1.std()
epf100_std = (epf100 - epf100.mean()) / epf100.std()

首先，我们制作一个标准化收益的散点图。

# 绘图
fig, axs = plt.subplots(1,2,figsize=(18,6))
axs[0].scatter(epf1_std, spy_std)
axs[0].set_xlabel('特征组合1')
axs[0].set_ylabel('SPY')
axs[1].scatter(epf100_std, spy_std)
axs[1].set_xlabel('特征组合100')
axs[1].set_ylabel('SPY')

特征组合的收益与 SPY ETF 的收益对比

我们可以清楚地看到，特征组合1（对应最大特征值）的收益与 SPY 的收益高度相关，而特征组合100（对应第100大的特征值）的收益与 SPY 的收益不相关。相关系数在下面计算。

收益相关性

我们也来绘制 SPY 和特征组合1的累计收益图。

# SPY 和特征组合1的累计收益
plt.figure(figsize=(18,6))
plt.plot((1 + epf1).cumprod(), label='特征组合1')
plt.plot((1 + spy).cumprod(), label='SPY')
plt.legend()

累计收益

如上图所示，累计收益几乎完全相匹配。收益存在差异的可能原因有两个：

• 我的股票组合并不完全与标普500指数相匹配。它包含了撰写时的标普500成分股，但在这五年期间标普500指数发生了许多变化——一些股票被剔除，其他股票被添加。
• 我们使用了整个时期的静态权重，但这些权重可能并不稳定，会随时间变化。

---

逆参与率

现在让我们使用逆参与率（IPR）来估计特征向量中显著参与者的数量。它的计算方式如下：

$I^k={\sum }_{l=1}^N{\left(u_l^k\right)}^4$

其中，$u_l^k$ 是第$k$ 个特征向量的第$l$ 个分量。

逆参与率（IPR）是一个用来量化特征向量分量的集中程度的指标。它反映了一个特征向量的分量中有多少是显著的，相较于分量平均分布的情况。一个高的IPR值意味着只有少数几个分量对特征向量有显著的贡献，而一个低的IPR值则意味着许多分量都在某种程度上对特征向量有贡献。

接下来，我将绘制随机相关矩阵和收益相关矩阵的逆参与率（IPR），并使用对数尺度。

# 随机样本（不相关）
rs = np.random.multivariate_normal(mean=returns.mean(), cov=np.diag(returns.var()), size=len(returns))
evals_rs, evecs_rs = np.linalg.eigh(np.corrcoef(rs.T))
ipr_rs = (evecs_rs**4).sum(axis=1)

# 实际收益
ipr = (evectors**4).sum(axis=1)

fig, axs = plt.subplots(1,2,figsize=(18,6))
axs[0].scatter(np.log10(evals_rs), np.log10(ipr_rs))
axs[0].fill_between([np.log10(lambda_minus), np.log10(lambda_plus)], -3, 0, alpha=0.2, label='RMT 界限')
axs[0].set_xlabel('特征值')
axs[0].set_ylabel('逆参与率')
axs[0].set_xlim(-3,3)
axs[0].set_ylim(-3,0)
axs[0].set_title('随机样本（不相关）')
axs[0].legend()
axs[1].scatter(np.log10(evalues), np.log10(ipr))
axs[1].fill_between([np.log10(lambda_minus), np.log10(lambda_plus)], -3, 0, alpha=0.2, label='RMT 界限')
axs[1].set_xlabel('特征值')
axs[1].set_ylabel('逆参与率')
axs[1].set_xlim(-3,3)
axs[1].set_ylim(-3,0)
axs[1].set_title('实际收益')
axs[1].legend()

随机样本与实际收益的IPR

左图展示了随机相关矩阵的IPR。所有特征值都在RMT界限内，所有IPR值大致相同。在随机矩阵中，所有特征向量分量的贡献类似，导致IPR较小。较大的IPR意味着特征向量有更少的显著成分。

右图展示了实际收益相关矩阵的IPR。注意，对应于最大特征值的向量与随机矩阵的IPR类似。这是有道理的——因为它代表市场，所有分量都是显著的。这部分与论文中的图11类似（如下所示）。但我们也有一些不同之处。注意，在论文中，RMT界限内的特征向量的IPR都彼此非常接近，也接近随机矩阵的IPR。在我们的图中，我们可以看到RMT界限内有许多较大的IPR。另一个不同之处是，论文中RMT界限以下的IPR都相对较大，但在我们的图中，大多数都接近随机矩阵的IPR。我不知道为什么会有这些差异，现在我将忽略它们。

特征值函数的IPR（图11）

---

有效前沿

接下来，我们可以尝试将所有这些应用于投资组合优化。这里的想法是通过仅保留高于RMT极限的最大特征值对应的信息来过滤相关矩阵。论文的第八节和图16描述了使用简单（未过滤）和过滤后的协方差矩阵构建的预测和实现的有效前沿。

首先，让我们尝试使用生成的数据。我使用生成的数据是为了确保其均值和协方差矩阵稳定，不会随时间改变。下面我生成了具有实际收益均值和方差的正态分布随机样本。然后我将生成的数据分为训练集和测试集。前四年用于训练（寻找最优投资组合），最后一年用于测试（计算最优投资组合的实现收益）。

# 生成数据
mean = returns.mean()
cov = returns.cov()

np.random.seed(1)
returns_sim = np.random.multivariate_normal(mean=mean, cov=cov, size=len(returns))
returns_sim = pd.DataFrame(returns_sim, index=returns.index, columns=returns.columns)

returns_train = returns_sim.loc['2018-01-01':'2021-12-31']
returns_test = returns_sim.loc['2022-01-01':'2022-12-31']
stocks = returns.columns

在文章开头，我承诺解释为什么我使用算术收益而不是论文中使用的对数收益。问题是我们需要算术收益来执行投资组合优化。论文中的方程式（23）和（24）仅对算术收益正确，对数收益则不适用。当然，我们可以轻松地将对数收益转换为算术收益，但问题是我们还需要将对数收益的过滤相关矩阵转换为算术收益的相关矩阵，这并不非常直接。虽然有一个公式可以做到这一点，但为了简单起见，我决定使用算术收益。

我不打算在这里描述整个投资组合优化程序。你可以在我的文章《投资组合优化和现代投资组合理论入门》中找到详细的解释。

下面你可以看到使用样本协方差矩阵计算的风险函数和预测与实现投资组合收益的图。

预测与实现的有效前沿

现在，让我们使用所学知识来计算过滤后的协方差矩阵。第一步是计算RMT界限${\lambda }_{+}$和${\lambda }_{-}$。

计算RMT界限

接下来我们对相关矩阵进行特征分解。回想一下，任何实对称矩阵A都可以分解为：

特征分解

然后我们将所有小于${\lambda }_{+}$的特征值设为零，并组装一个新的（过滤后的）矩阵。为了使其成为有效的相关矩阵，我们将所有对角线元素设为1。最后我们将相关矩阵转换为协方差矩阵，用于投资组合优化。

corr = returns_train.corr()

# 特征值分解
evalues,evectors = np.linalg.eigh(corr.values)

# 过滤后的相关矩阵
evalues[evalues<=lambda_plus] = 0
corr_filt = pd.DataFrame(evectors @ np.diag(evalues) @ evectors.T, index=corr.index, columns=corr.columns)
np.fill_diagonal(corr_filt.values, 1)

# 将相关矩阵转换为协方差矩阵
D = np.diag(returns_train.std())
cov_filt = D @ corr_filt @ D

结果在下面绘制。我们的图与论文中的图16类似。我们可以看到，当我们使用过滤后的协方差矩阵时，实现的收益比预测的更接近。

预测与实现的有效前沿

回想一下，我使用生成的数据进行了这个测试。现在让我们尝试使用实际收益重复同样的过程。所有代码都是相同的，所以我只展示结果。

比较预测与实现的有效前沿

回想一下，我使用生成的数据进行了这个测试。现在让我们尝试使用实际收益重复同样的过程。所有代码都是相同的，所以我只展示结果。

预测与实现的有效前沿（真实数据）

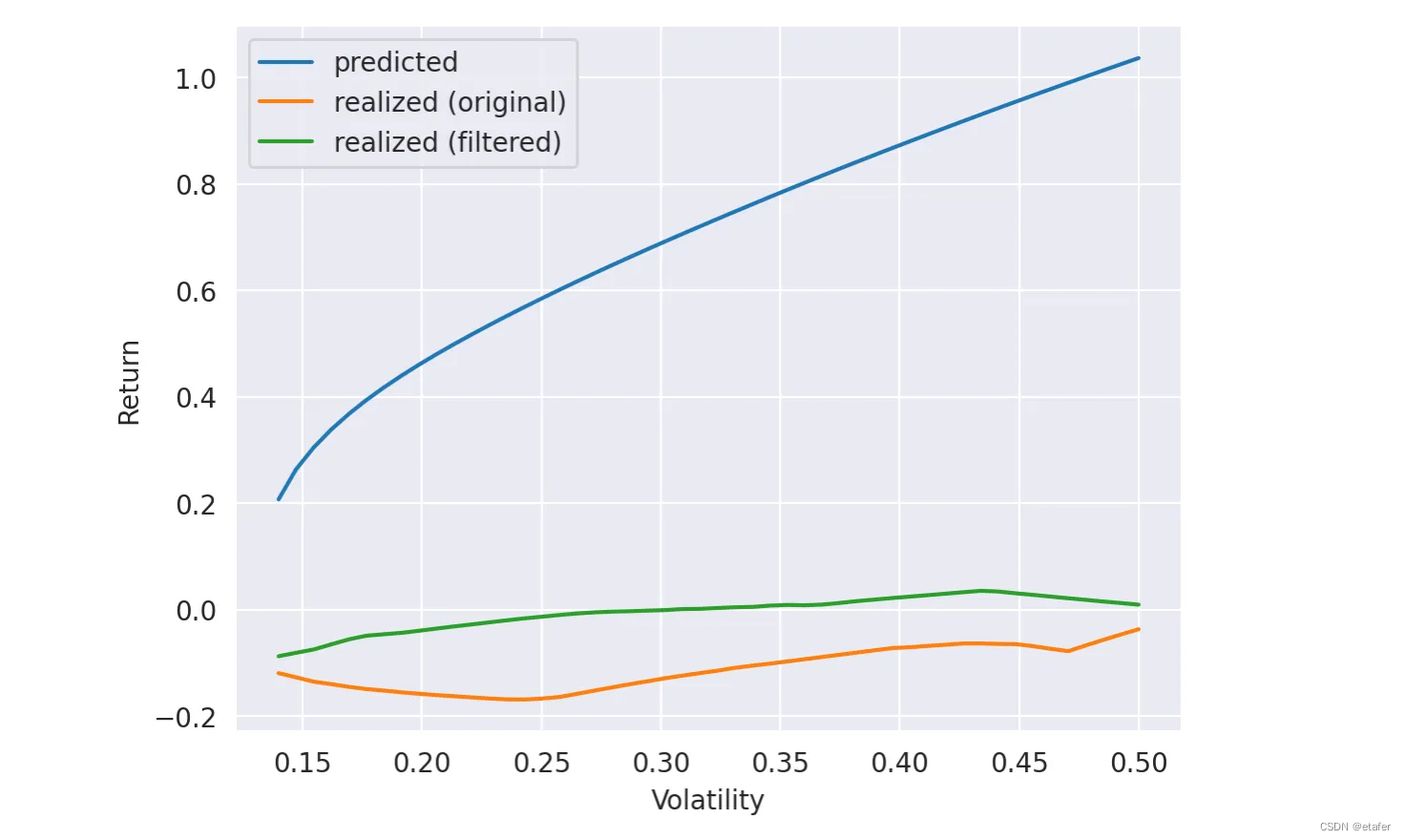
在这里，我们可以清楚地看到，使用过滤后的协方差矩阵得到的曲线比使用完整样本协方差矩阵得到的曲线更接近预测曲线。使用上述相同的度量，我们得到以下结果。

比较预测与实现的有效前沿

---

策略回测

最后，我们准备创建并回测一个交易策略。我将使用相同的数据。投资组合将每周重新平衡，我将使用252天的滚动窗口来估计均值和协方差矩阵。

首先，让我们计算等权重投资组合的绩效指标。

# 准备每周数据
prices.index = pd.to_datetime(prices.index)
prices_w = prices.resample('1W').last()
returns_w = prices_w.pct_change().dropna()

# 等权重投资组合
cumret_eqw = (1 + returns_w.loc['2019-01-01':].sum(axis=1)/returns.shape[1]).cumprod()

results_df = pd.DataFrame(columns = ['总回报', '年化收益率', '夏普比率', '最大回撤', '最大回撤持续时间'])
results_df.loc['等权重'] = calculate_metrics(cumret_eqw)

绩效指标

回想一下，我们需要指定目标波动率来执行带有MPT的投资组合优化。我将使用等权重投资组合的波动率。它的计算如下。

等权重投资组合的波动率

接下来，我们回测一个使用简单（未过滤）协方差矩阵的策略。其绩效指标如下所示。我们可以看到这个策略在回报方面超过了等权重投资组合，但夏普比率略低，回撤更大。

# 使用简单（滚动）协方差矩阵的MPT
positions = pd.DataFrame(index=returns_w.loc['2019-01-01':].index, columns=returns_w.columns)

目标波动率 = volatility_eqw
bounds=[[0,1]]*len(stocks)
x0 = np.ones(len(stocks)) / len(stocks)

for t in tqdm(returns_w.loc['2019-01-01':].index):
    # 准备数据
    prices_tmp = prices.loc[:t].iloc[-252:]
    returns_tmp = prices_tmp.pct_change().dropna()
    
    # 执行优化
    constraints = ({'type':'eq', 'fun': lambda x: volatility(x,returns_tmp.cov())-target_vol}, 
                   {'type':'eq', 'fun': lambda x: np.sum(x)-1})
    res = minimize(negative_annual_return, x0, args=(returns_tmp.mean()), 
               bounds=bounds, constraints=constraints)
    if res.status!=0:
        print('优化失败')
        positions.loc[t] = positions.loc[:t].iloc[-2] # 保持之前的权重
    else:
        positions.loc[t] = res.x

cumret_simple_cov = (1 + (positions.shift() * returns_w.loc['2019-01-01':]).sum(axis=1)).cumprod()
results_df.loc['MPT（简单协方差）'] = calculate_metrics(cumret_simple_cov)

绩效指标

现在我们将实现并回测一个使用过滤后协方差矩阵的策略。一切都是相同的，我们只需要执行特征值分解并计算过滤后的协方差矩阵，然后用它来进行均值-方差优化。

# 使用过滤后协方差矩阵的策略
positions = pd.DataFrame(index=returns_w.loc['2019-01-01':].index, columns=returns_w.columns)

目标波动率 = volatility_eqw
bounds=[[0,1]]*len(stocks)
x0 = np.ones(len(stocks)) / len(stocks)

for t in tqdm(returns_w.loc['2019-01-01':].index):
    # 准备数据
    prices_tmp = prices.loc[:t].iloc[-252:]
    returns_tmp = prices_tmp.pct_change().dropna()
    
    # 寻找特征值的上界
    Q = returns_tmp.shape[0] / returns_tmp.shape[1]
    lambda_plus = 1 + 1/Q + 2*np.sqrt(1/Q)
    
    # 执行特征值分解
    corr = returns_tmp.corr()
    evalues, evectors = np.linalg.eigh(corr)
    
    # 构建过滤后的相关矩阵
    evalues[evalues<=lambda_plus] = 0
    corr_filt = pd.DataFrame(evectors @ np.diag(evalues) @ evectors.T, index=corr.index, columns=corr.columns)
    np.fill_diagonal(corr_filt.values, 1)
    
    # 将相关矩阵转换为协方差矩阵
    D = np.diag(returns_tmp.std())
    cov_filt = D @ corr_filt @ D
    
    # 使用过滤后的协方差矩阵进行优化
    constraints = ({'type':'eq', 'fun': lambda x: volatility(x,cov_filt)-target_vol}, 
                   {'type':'eq', 'fun': lambda x: np.sum(x)-1})
    res = minimize(negative_annual_return, x0, args=(returns_tmp.mean()), 
               bounds=bounds, constraints=constraints)
    if res.status!=0:
        print('优化失败')
        positions.loc[t] = positions.loc[:t].iloc[-2] # 保持之前的权重
    else:
        positions.loc[t] = res.x

cumret_filtered_cov = (1 + (positions.shift() * returns_w.loc['2019-01-01':]).sum(axis=1)).cumprod()
results_df.loc['MPT（过滤后协方差）'] = calculate_metrics(cumret_filtered_cov)

绩效指标

最后的策略拥有最高的回报，并且其回撤持续时间显著较短（40周而不是其他策略的52\59周）。它的夏普比率稍低，但请记住我们是为了最大回报而优化，而不是夏普比率。另一个好处是，使用过滤后的协方差矩阵进行均值-方差优化速度更快 —— 在我的服务器上，回测使用过滤后协方差矩阵的策略大约比使用完整样本协方差的策略快2.5倍。

---

总结

我们已经证明，使用随机矩阵理论（RMT）来估计收益协方差矩阵可以提高最优投资组合的表现。它帮助我们区分真实相关性与随机相关性，即使在随机无相关样本的相关矩阵中也存在这些随机相关性。

我所进行的一些测试的结果与论文中呈现的结果不匹配。需要进一步的研究来解释这些差异，并可能引入一些改进来提高过滤后协方差矩阵的准确性。

包含源代码的Jupyter notebook可在此处获取。

---

引用

[1] 《金融数据中的交叉相关性的随机矩阵方法》（Plerou 等，2001年）

[2] 随机矩阵

[3] 投资组合优化核现代投资组合理论

[4] 使用加权均值和协方差估计器的投资组合优化

[5] https://mathoverflow.net/questions/386493/distribution-of-eigenvectors-of-random-matrices-and-link-with-the-components-of

[6] https://quant.stackexchange.com/questions/70997/how-to-calculate-the-log-return-of-portfolio

[7] https://quant.stackexchange.com/questions/76688/calculating-portfolios-covariance-via-bilinearity-with-log-or-simple-return