【2025】最强总结！十大时间序列模型 ！！

于 2025-04-17 10:54:37 发布
阅读量1.6k 收藏 30
点赞数 26
分类专栏： 人工智能 深度学习 神经网络 文章标签： 人工智能 时序数据库 计算机视觉 时间序列 目标检测 神经网络 机器学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/gu781223/article/details/147295427
版权

今天就把最最常见的时间序列算法和大家聊聊~

大家都理解的是，时间序列分析能够为未来的预测提供科学依据。它帮助识别和量化数据中的模式和周期性变化，从而优化决策过程。通过精准的时间序列模型，企业和组织能够提高效率、降低风险，并做出更具前瞻性的战略规划。

后面文中有些代码的图没有体现出来，大家可以自行跑代码查看效果~

今天和大家分享的时间序列算法模型有：

  • 自回归模型

  • 移动平均模型

  • 自回归移动平均模型

  • 自回归积分移动平均模型

  • 季节性自回归积分移动平均模型

  • 向量自回归模型

  • 条件异方差模型

  • 广义条件异方差模型

  • 长短期记忆网络

  • Prophet模型

1. 自回归模型

原理

自回归模型 (Autoregressive Model, AR) 是一种基于过去的时间序列数据预测未来的统计模型。它假设当前值是过去若干时刻值的线性组合，并加入一个白噪声项。

核心公式

AR模型的核心公式为：

  • 当前时刻的值

  • 模型的回归系数

  • 模型的阶数 (使用过去多少个时刻的数据)

  •  白噪声，服从正态分布 

推导：

  1. 假设时间序列是平稳的，均值和方差恒定。

  2. 通过最小二乘法或 Yule-Walker 方程估计参数 。

  3. 预测值通过历史值和模型参数的线性组合计算。

优缺点和适用场景

优点：

  • 模型简单，易于实现和解释。

  • 适合处理平稳时间序列。

缺点：

  • 无法处理非平稳数据，需要先进行差分处理。

  • 仅考虑自回归关系，不能处理复杂的时间依赖性。

适用场景：

  • 股票价格的短期预测。

  • 气象数据的平稳部分建模。

核心案例

下面的代码生成一个虚拟时间序列，使用 AR(2) 模型进行拟合和预测，并绘制两个图：

  1. 时间序列实际值与拟合值对比图。

  2. 残差分布图，展示模型是否符合白噪声假设。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.ar_model import AutoReg
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 生成虚拟时间序列数据
np.random.seed(42)
n = 200
phi1, phi2 = 0.7, -0.2
noise = np.random.normal(0, 1, n)
data = [0, 0]  # 初始值
for t in range(2, n):
    data.append(phi1 * data[t-1] + phi2 * data[t-2] + noise[t])

# 转换为 Pandas DataFrame
time_series = pd.Series(data, name="Time Series")

# 拟合 AR(2) 模型
model = AutoReg(time_series, lags=2)
model_fit = model.fit()
fitted_values = model_fit.fittedvalues
residuals = time_series[2:] - fitted_values

# 绘制分析图
plt.figure(figsize=(12, 6))

# 图 1: 时间序列实际值与拟合值对比
plt.subplot(1, 2, 1)
plt.plot(time_series[2:], label="Actual Data", color="blue", alpha=0.7)
plt.plot(fitted_values, label="Fitted Data", color="red", linestyle="--")
plt.title("Actual vs Fitted Data", fontsize=14)
plt.legend()

# 图 2: 残差分析图
plt.subplot(1, 2, 2)
plt.hist(residuals, bins=20, color="purple", alpha=0.7, edgecolor="black")
plt.axvline(x=0, color="black", linestyle="--", linewidth=1)
plt.title("Residual Distribution", fontsize=14)
plt.xlabel("Residuals")
plt.ylabel("Frequency")

plt.tight_layout()
plt.show()

实际值与拟合值对比图：展示模型的拟合效果。拟合值越接近实际值，说明模型预测能力越强。

残差分布图：分析残差是否近似正态分布。若残差无明显趋势且服从正态分布，说明模型假设合理。

通过这两个图，可以验证 AR(2) 模型是否适合描述数据的动态特性。如果发现残差分布偏离正态分布或拟合效果差，则可能需要调整阶数或改用其他模型。

2. 移动平均模型

原理

移动平均模型 (Moving Average, MA) 是一种线性时间序列模型，假设当前值是过去若干随机误差项的线性组合。与自回归模型不同，MA 模型不直接依赖过去的观测值，而是依赖过去误差项对当前值的影响。

核心公式

MA 模型的核心公式为：

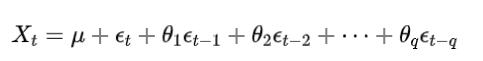
  • : 当前时刻的值

  • : 时间序列的均值

  • : 当前时刻的白噪声（随机误差），服从正态分布 

  • : 模型的参数

  • : 模型的阶数 (过去影响当前的误差项数量)

推导：

  1. 假设时间序列是平稳的。

  2. 模型中的  是不可观测的，通过最大似然估计法或最小二乘法估计  参数。

  3. 预测值通过过去的误差项和模型参数的线性组合计算。

优缺点和适用场景

优点：

  • 模型简单，适合描述白噪声对当前值的直接影响。

  • 对于非平稳时间序列的短期建模有效。

缺点：

  • 无法捕获长期依赖关系。

  • 阶数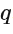的选择较为复杂，过大可能导致过拟合。

适用场景：

  • 短期销量预测。

  • 信号处理中的噪声滤除。

核心案例

下面的代码模拟一个 MA(3) 模型，拟合数据并进行残差分析：

  1. 实际时间序列与模型拟合值对比图。

  2. 残差的自相关函数 (ACF) 图，验证残差是否为白噪声。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf

# 生成虚拟时间序列数据
np.random.seed(42)
n = 200
theta1, theta2, theta3 = 0.6, -0.4, 0.2
noise = np.random.normal(0, 1, n)
data = []
for t in range(n):
    term = noise[t]
    if t > 0:
        term += theta1 * noise[t-1]
    if t > 1:
        term += theta2 * noise[t-2]
    if t > 2:
        term += theta3 * noise[t-3]
    data.append(term)

# 转换为 Pandas DataFrame
time_series = pd.Series(data, name="Time Series")

# 拟合 MA(3) 模型
model = ARIMA(time_series, order=(0, 0, 3))  # ARIMA 的 AR=0, I=0, MA=3
model_fit = model.fit()
fitted_values = model_fit.fittedvalues
residuals = model_fit.resid

# 绘制分析图
plt.figure(figsize=(12, 6))

# 图 1: 实际值与拟合值对比图
plt.subplot(1, 2, 1)
plt.plot(time_series, label="Actual Data", color="blue", alpha=0.7)
plt.plot(fitted_values, label="Fitted Data", color="orange", linestyle="--")
plt.title("Actual vs Fitted Data", fontsize=14)
plt.legend()

# 图 2: 残差的自相关函数 (ACF) 图
plt.subplot(1, 2, 2)
plot_acf(residuals, lags=20, ax=plt.gca(), color="purple")
plt.title("ACF of Residuals", fontsize=14)

plt.tight_layout()
plt.show()

实际值与拟合值对比图：直观对比模型的拟合效果。若拟合值与实际值接近，说明模型捕获了时间序列的主要特征。

残差的自相关函数 (ACF) 图：验证残差是否为白噪声。如果 ACF 显示在大多数滞后下无显著相关性（即接近零），说明残差符合白噪声假设。

通过这两个图可以判断 MA 模型的有效性。若发现残差的自相关显著，则需要调整阶数  或改用更复杂的模型。

3. 自回归移动平均模型

原理

自回归移动平均模型 (Autoregressive Moving Average, ARMA) 是时间序列分析中的经典模型，结合了自回归 (AR) 和移动平均 (MA) 的思想，能够同时建模时间序列的自相关性和随机误差的影响。

  • 自回归部分 (AR)：当前值是过去观测值的线性组合。

  • 移动平均部分 (MA)：当前值是过去误差项的线性组合。

核心公式

ARMA(p, q) 模型的核心公式为：

  • : 当前时刻的值

  • : AR 部分的系数

  • : MA 部分的系数

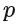  • : 自回归阶数

  • : 移动平均阶数

  • 当前白噪声误差项

推导：

  1. 建立时间序列模型假设，选择P和q阶数。

  2. 使用 ACF（自相关函数）和 PACF（偏自相关函数）确定 AR 和 MA 的阶数。

  3. 最大似然估计参数

  4. 结合 AR 和 MA 的特性预测未来值。

优缺点和适用场景

优点：

  • 能同时捕捉时间序列的自相关性和误差项的随机波动。

  • 适合平稳时间序列的中短期预测。

缺点：

  • 模型参数较多，选择合适的  和  较复杂。

  • 对非平稳时间序列需要先进行差分处理。

适用场景：

  • 气象数据建模（如温度波动）。

  • 金融市场指数分析。

核心案例

使用虚拟气温数据集进行建模和预测，分析：

  1. 时间序列分解图。

  2. 模型残差的正态性与序列性分析。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.seasonal import seasonal_decompose
from scipy.stats import probplot

# 生成虚拟气温数据 (季节性+趋势+噪声)
np.random.seed(42)
n = 300
t = np.arange(n)
trend = 0.05 * t  # 线性趋势
seasonal = 10 * np.sin(2 * np.pi * t / 50)  # 周期性
noise = np.random.normal(0, 2, n)  # 噪声
data = trend + seasonal + noise
time_series = pd.Series(data, name="Temperature")

# 绘制时间序列分解图
result = seasonal_decompose(time_series, model="additive", period=50)
result.plot()
plt.suptitle("Time Series Decomposition", fontsize=16)
plt.tight_layout()
plt.show()

# ARMA 模型拟合 (选择 ARMA(3, 2))
model = ARIMA(time_series, order=(3, 0, 2))  # 注意 d=0，因为数据平稳
model_fit = model.fit()
fitted_values = model_fit.fittedvalues
residuals = model_fit.resid

# 绘制分析图
plt.figure(figsize=(12, 6))

# 图 1: 时间序列拟合与实际值对比
plt.subplot(1, 2, 1)
plt.plot(time_series, label="Actual Data", color="blue", alpha=0.7)
plt.plot(fitted_values, label="Fitted Data", color="red", linestyle="--")
plt.title("Actual vs Fitted Data", fontsize=14)
plt.legend()

# 图 2: 残差的正态性分析 (QQ图)
plt.subplot(1, 2, 2)
probplot(residuals, dist="norm", plot=plt)
plt.title("Residuals QQ Plot", fontsize=14)

plt.tight_layout()
plt.show()

  1. 时间序列分解图：显示时间序列的趋势、季节性和随机成分，帮助判断是否需要进行平稳化处理。在本例中，时间序列是平稳的，因此 。

  2. 实际值与拟合值对比图：说明 ARMA(3, 2) 模型能有效捕捉时间序列的动态特性。

  3. 残差的 QQ 图：验证残差是否服从正态分布。如果点接近直线，说明模型假设合理。

通过这种分析方法，可以全面评估 ARMA 模型的适配性，并针对时间序列的特性调整阶数或改用更复杂的模型。

4. 自回归积分移动平均模型

原理

自回归积分移动平均模型 (Autoregressive Integrated Moving Average, ARIMA) 是一种扩展了 ARMA 的时间序列分析模型，适用于非平稳时间序列。通过差分操作将非平稳序列转化为平稳序列，再使用 ARMA 模型进行建模。

  • 自回归部分 (AR)：当前值是过去观测值的线性组合。

  • 移动平均部分 (MA)：当前值是过去误差项的线性组合。

  • 积分部分 (I)：通过差分将非平稳数据转化为平稳数据。

核心公式

ARIMA(p, d, q) 模型：

  • p: 自回归阶数。

  • d: 差分次数。

  • q: 移动平均阶数。

推导：

1. 差分：通过一次或多次差分，将原始非平稳时间序列  转换为平稳序列 。

  • 一阶差分：

  • 二阶差分：

2. 平稳化后的建模：对平稳序列使用 ARMA(p, q) 模型，结合 AR 和 MA 的特性进行预测。

3. 参数估计：利用 ACF 和 PACF 图选择  和 ，差分阶数  根据单位根检验决定。

优缺点和适用场景

优点：

  • 适合处理非平稳数据，具有很强的灵活性。

  • 广泛应用于各类时间序列预测任务。

缺点：

  • 参数  的选择较复杂，需要借助统计检验和图表辅助。

  • 对长时间序列更适用，短期数据建模效果有限。

适用场景：

  • 股票市场价格预测。

  • 经济指标（如 GDP、CPI）分析。

  • 科学实验数据序列分析。

核心案例

使用虚拟经济指数时间序列，进行 ARIMA 建模和预测：

  1. 一阶差分的时间序列图，展示数据平稳化过程。

  2. 实际值与预测值的对比图。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 生成虚拟经济指数数据（非平稳时间序列）
np.random.seed(42)
n = 300
t = np.arange(n)
trend = 0.5 * t  # 增长趋势
seasonal = 10 * np.sin(2 * np.pi * t / 50)  # 周期性
noise = np.random.normal(0, 2, n)  # 噪声
data = trend + seasonal + noise
time_series = pd.Series(data, name="Economic Index")

# 一阶差分
diff_series = time_series.diff().dropna()

# 绘制差分序列和原始序列对比图
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(time_series, label="Original Data", color="blue")
plt.title("Original Economic Index", fontsize=14)
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(diff_series, label="Differenced Data", color="green")
plt.title("First Difference", fontsize=14)
plt.legend()
plt.tight_layout()
plt.show()

# ARIMA 模型拟合 (选择 ARIMA(2, 1, 2))
model = ARIMA(time_series, order=(2, 1, 2))
model_fit = model.fit()
forecast = model_fit.predict(start=len(time_series), end=len(time_series) + 20, typ='levels')
fitted_values = model_fit.fittedvalues

# 绘制实际值与预测值对比图
plt.figure(figsize=(12, 6))
plt.plot(time_series, label="Actual Data", color="blue", alpha=0.7)
plt.plot(fitted_values, label="Fitted Data", color="red", linestyle="--")
plt.plot(np.arange(len(time_series), len(time_series) + len(forecast)), forecast, label="Forecast", color="purple")
plt.title("Actual vs Fitted Data with Forecast", fontsize=14)
plt.legend()
plt.show()

  1. 差分序列图：展示原始数据的一阶差分，验证平稳性。差分后的数据波动幅度稳定且均值恒定，表明差分有效。

  2. 实际值与预测值对比图：评估 ARIMA(2, 1, 2) 模型的拟合和预测效果。若预测值紧随实际值变化，说明模型捕捉了数据特性；未来预测显示模型的外推能力。

通过差分分析和平稳性检验，可以确认数据是否需要差分处理，并选择适合的 。通过实际与预测值对比，可以验证 ARIMA 模型对非平稳序列的建模效果。

5. 季节性自回归积分移动平均模型

原理

季节性自回归积分移动平均模型 (Seasonal ARIMA, SARIMA) 是在 ARIMA 模型的基础上引入季节性成分，以处理存在周期性特征的时间序列数据。

SARIMA 模型通过季节性自回归、季节性差分、季节性移动平均等扩展部分捕捉季节性规律，同时保留 ARIMA 模型的基础能力。

核心公式

SARIMA 模型的表示为 核心公式：

 

常规部分：

季节性部分：

推导：

  1. 季节性差分：通过季节性差分 ，消除周期性趋势。

  2. 非季节性建模：对剩余数据应用常规 ARIMA 模型进行建模。

  3. 参数估计：通过 ACF 和 PACF 图确定季节性和非季节性部分的阶数。

优缺点和适用场景

优点：

  • 专门处理季节性数据，能同时捕捉季节性规律和非季节性变化。

  • 应用广泛，适合具有明显周期性特征的时间序列。

缺点：

  • 模型复杂，参数较多。

  • 对数据预处理要求较高，如需充分平稳化处理。

适用场景：

  • 零售销量（如节假日销售波动）。

  • 气象数据（如月度温度变化）。

  • 旅游数据（如季度游客流量）。

核心案例

使用虚拟的月度零售销量数据进行 SARIMA 建模和分析：

  1. 季节性差分序列图，展示消除季节性的效果。

  2. 实际值与预测值对比图。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 生成虚拟月度零售数据（季节性+趋势+噪声）
np.random.seed(42)
n = 120
t = np.arange(n)
trend = 5 + 0.1 * t  # 线性趋势
seasonal = 10 * np.sin(2 * np.pi * t / 12)  # 年周期性
noise = np.random.normal(0, 3, n)  # 噪声
data = trend + seasonal + noise
time_series = pd.Series(data, index=pd.date_range(start='2010-01', periods=n, freq='M'), name="Monthly Sales")

# 季节性差分
seasonal_diff = time_series.diff(12).dropna()

# 绘制季节性差分序列和原始序列对比图
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(time_series, label="Original Data", color="blue")
plt.title("Original Time Series", fontsize=14)
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(seasonal_diff, label="Seasonally Differenced Data", color="green")
plt.title("Seasonally Differenced Series", fontsize=14)
plt.legend()
plt.tight_layout()
plt.show()

# SARIMA 模型拟合 (SARIMA(1, 1, 1)(1, 1, 1, 12))
model = SARIMAX(time_series, order=(1, 1, 1), seasonal_order=(1, 1, 1, 12))
model_fit = model.fit()
forecast = model_fit.get_forecast(steps=24)
forecast_index = pd.date_range(start=time_series.index[-1] + pd.offsets.MonthBegin(1), periods=24, freq='M')
forecast_values = forecast.predicted_mean

# 绘制实际值与预测值对比图
plt.figure(figsize=(12, 6))
plt.plot(time_series, label="Actual Data", color="blue", alpha=0.7)
plt.plot(forecast_index, forecast_values, label="Forecast", color="orange", linestyle="--")
plt.title("Actual vs Forecast Data", fontsize=14)
plt.legend()
plt.show()

  1. 季节性差分序列图：展示原始数据和季节性差分数据对比。差分后序列波动趋于稳定，表明季节性差分有效。

  2. 实际值与预测值对比图：展示 SARIMA 模型对零售数据的预测效果。预测值紧随实际值变化，且模型捕捉到未来的周期性波动。

SARIMA 模型在处理具有明显周期性规律的数据时非常有效，通过差分分析和预测值的对比，可以全面评估模型的适用性和预测能力。

6. 向量自回归模型

原理

向量自回归模型 (Vector Autoregressive Model, VAR) 是一种多变量时间序列模型，用于建模多个时间序列变量之间的相互依赖关系。与 AR 模型不同，VAR 模型处理的是多个相关时间序列，能够捕捉它们之间的动态互动。

在 VAR 模型中，每个时间序列的值不仅是自身过去值的函数，还与其他时间序列的过去值有关。

核心公式

假设我们有两个时间序列变量  和它们的滞后值构成的向量自回归模型，VAR(p) 模型的核心公式为：

  • : 当前时刻的多变量值向量。

  • : 常数项（截距）。

  • : 自回归系数矩阵（描述不同变量之间的滞后关系）。

  • : 滞后阶数。

  • : 白噪声误差项。

推导：

  1. 模型选择：根据数据的特征选择滞后阶数 。

  2. 最小二乘法估计：利用历史数据对模型中的系数进行估计。

  3. 模型验证：通过残差分析、Granger因果检验等方法验证模型拟合效果。

优缺点和适用场景

优点：

  • 可以处理多个时间序列的相互依赖关系，适用于多变量预测问题。

  • 能捕捉变量之间的动态交互，特别适用于经济、金融等领域。

缺点：

  • 模型参数较多，当变量过多时可能需要大量的样本数据。

  • 对于长时间序列，可能会受到噪声的影响。

适用场景：

  • 宏观经济数据分析（如 GDP、失业率、通货膨胀等的相互关系）。

  • 金融市场（如股市、汇率、利率之间的关系）。

  • 供应链管理（如原料采购量与产品销售量的关系）。

核心案例

使用虚拟的股市数据（如股票价格和交易量），进行 VAR 建模和分析：

  1. 原始数据图，展示股票价格和交易量的变化趋势。

  2. Granger因果检验结果和预测结果对比图。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.api import VAR
from statsmodels.tsa.stattools import grangercausalitytests
from statsmodels.graphics.tsaplots import plot_pacf, plot_acf

# 生成虚拟股市数据（股票价格和交易量）
np.random.seed(42)
n = 200
t = pd.date_range(start="2020-01-01", periods=n, freq="D")
price = 50 + 0.05 * np.cumsum(np.random.randn(n))  # 股票价格
volume = 5000 + 20 * np.cumsum(np.random.randn(n))  # 交易量
data = pd.DataFrame({"Price": price, "Volume": volume}, index=t)

# 绘制原始数据图
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(data['Price'], label="Stock Price", color="blue")
plt.title("Stock Price", fontsize=14)
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(data['Volume'], label="Trading Volume", color="green")
plt.title("Trading Volume", fontsize=14)
plt.legend()

plt.tight_layout()
plt.show()

# 建立 VAR 模型 (选择滞后阶数 p=5)
model = VAR(data)
model_fitted = model.fit(5)

# Granger因果检验 (检验 Volume 是否是 Price 的因果变量)
gc_test = grangercausalitytests(data, maxlag=5, verbose=True)

# 进行未来 10 天的预测
forecast = model_fitted.forecast(data.values[-5:], steps=10)
forecast_df = pd.DataFrame(forecast, index=pd.date_range(start=data.index[-1] + pd.Timedelta(days=1), periods=10, freq='D'), columns=data.columns)

# 绘制预测结果对比图
plt.figure(figsize=(12, 6))
plt.plot(data['Price'], label="Historical Stock Price", color="blue")
plt.plot(forecast_df['Price'], label="Forecasted Stock Price", color="orange", linestyle="--")
plt.title("Actual vs Forecasted Stock Price", fontsize=14)
plt.legend()
plt.show()

  1. 原始数据图：展示了股票价格和交易量的变化趋势。通过这些图可以观察到两个变量之间的潜在关系，并为 VAR 模型的建立提供直观依据。

  2. Granger因果检验结果：用于检验交易量是否对股票价格具有因果影响。在检验结果中，如果某个滞后阶数下的 p 值小于显著性水平（通常为 0.05），则表示交易量对股票价格有显著的因果影响。

  3. 实际值与预测值对比图：展示了 VAR 模型对未来股市数据的预测效果，能够观察模型是否能准确捕捉到股票价格的变化趋势。

通过 VAR 模型可以有效地捕捉到多个时间序列变量之间的动态关系，并通过 Granger因果检验来进一步分析变量之间的因果关系。

7. 条件异方差模型

原理

条件异方差模型（Autoregressive Conditional Heteroskedasticity, ARCH）及其扩展模型（Generalized Autoregressive Conditional Heteroskedasticity, GARCH）用于建模时间序列数据的方差不稳定性，尤其是在金融时间序列数据中，波动性随着时间变化而变化。它们考虑到当下的条件方差（即误差的波动性）取决于过去的信息。

  • ARCH 模型：假设当前的方差由过去误差的平方值决定。

  • GARCH 模型：扩展了 ARCH 模型，假设当前的方差不仅由过去的误差项，还由过去的方差项决定。

核心公式

ARCH(p) 模型：假设条件方差是过去  个误差项平方的线性组合：

  • : 当前时间点的观测值。

  • : 均值。

  • : 残差（误差项）。

  • : 条件方差。

  • : ARCH 模型的参数。

GARCH(p, q) 模型：假设当前的条件方差不仅依赖于过去的误差项，还依赖于过去的方差：

  • : GARCH 模型的参数（控制过去方差的影响）。

推导：

  1. 模型选择：通过模型的拟合优度（如AIC、BIC）选择合适的阶数  和 。

  2. 参数估计：使用最大似然估计方法对  和  进行估计。

  3. 模型验证：通过残差诊断、拟合度检验等方法验证模型拟合效果。

优缺点和适用场景

优点：

  • 专门处理金融时间序列中常见的波动性聚集现象（即高波动期和低波动期交替出现）。

  • 能有效捕捉时间序列中的波动性变化。

缺点：

  • 模型复杂度较高，需要较长时间序列数据。

  • 需要对数据进行充分的预处理和检验，以确保模型的有效性。

适用场景：

  • 金融市场（如股价波动率建模、外汇市场的波动预测）。

  • 风险管理和资产定价（如 VaR 计算）。

  • 宏观经济变量的波动性建模（如 GDP、CPI 等经济指标的波动分析）。

核心案例

使用虚拟的股票价格数据，进行 GARCH 模型的建模和分析：

  1. 股票价格的波动性图（条件方差的变化趋势）。

  2. 股票收益率与条件方差的关系图。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from arch import arch_model
from statsmodels.tsa.stattools import adfuller

# 生成虚拟股票价格数据（随机游走模型）
np.random.seed(42)
n = 1000
returns = np.random.randn(n)  # 正态分布的收益率数据
price = 100 + np.cumsum(returns)  # 模拟股票价格
time_series = pd.Series(price, name="Stock Price")

# 计算收益率
stock_returns = np.diff(np.log(time_series)) * 100  # 对数收益率（百分比）
stock_returns = pd.Series(stock_returns, index=time_series.index[1:], name="Stock Returns")

# 绘制收益率的时间序列图
plt.figure(figsize=(12, 6))
plt.plot(stock_returns, label="Stock Returns", color="blue")
plt.title("Stock Returns Time Series", fontsize=14)
plt.legend()
plt.show()

# 检验收益率序列是否平稳（ADF检验）
adf_result = adfuller(stock_returns.dropna())
print(f"ADF Statistic: {adf_result[0]}")
print(f"p-value: {adf_result[1]}")

# GARCH(1, 1) 模型拟合
model = arch_model(stock_returns, vol='Garch', p=1, q=1)
model_fit = model.fit()

# 获取拟合的条件方差
conditional_volatility = model_fit.conditional_volatility

# 绘制条件方差（波动率）的变化趋势
plt.figure(figsize=(12, 6))
plt.plot(conditional_volatility, label="Conditional Volatility (GARCH)", color="red")
plt.title("Conditional Volatility over Time", fontsize=14)
plt.legend()
plt.show()

# 绘制收益率与条件方差的关系
plt.figure(figsize=(12, 6))
plt.scatter(stock_returns, conditional_volatility, color="green", alpha=0.5)
plt.title("Stock Returns vs Conditional Volatility", fontsize=14)
plt.xlabel("Stock Returns")
plt.ylabel("Conditional Volatility")
plt.show()

  1. 收益率的时间序列图：展示了模拟的股票收益率数据的波动性。可以看到，收益率波动较大，具有波动性聚集的特点，可能在某些时段出现大幅波动。

  2. 条件方差（波动率）的变化趋势图：展示了通过 GARCH(1, 1) 模型拟合得到的条件方差（即股票收益率的波动性）。可以观察到波动性随着时间的变化而变化，并在某些时段出现了波动性聚集现象。

  3. 收益率与条件方差的关系图：展示了股票收益率与模型拟合出的条件方差之间的关系。通过散点图可以看到，极端的收益率（正负大波动）对应较高的条件方差，表明在高波动期，市场的波动性较大。

条件异方差模型（如 ARCH 和 GARCH）能够有效地捕捉到金融市场中常见的波动性聚集现象。

8. 广义条件异方差模型

原理

广义条件异方差模型（Generalized Autoregressive Conditional Heteroskedasticity, GARCH）是 ARCH 模型的扩展，它将当前的条件方差不仅由过去的误差项（ARCH）决定，还考虑了过去的条件方差（GARCH）。这类模型通过引入更多的滞后项来更好地描述金融市场中常见的波动性变化。

GARCH(p, q) 模型：包含  个滞后的误差项和  个滞后的条件方差项。

**EGARCH (Exponential GARCH)**：EGARCH 模型通过对条件方差建模时引入对数函数，能够处理金融数据中“杠杆效应”（即负面新闻对市场波动的影响大于正面新闻）。

TGARCH (Threshold GARCH) 和 **GJR-GARCH (Glosten-Jagannathan-Runkle GARCH)**：这些模型引入了阈值效应（如负面冲击的影响大于正面冲击），更准确地捕捉到非对称性。

其中  是指示函数，表示负的收益率对波动性的影响。

核心公式

GARCH(p, q) 模型:

EGARCH 模型:

TGARCH/GJR-GARCH 模型:

优缺点和适用场景

优点：

  • 适用于具有异方差性质的数据，能够捕捉数据的波动性变化。

  • 能够建模金融市场中常见的波动性聚集现象和非对称效应。

  • 扩展模型（如EGARCH和TGARCH）可以更好地处理不同类型的冲击（例如负面冲击对波动的影响较大）。

缺点：

  • 对数据的平稳性有要求，需要对时间序列进行必要的检验。

  • 参数估计和模型选择可能较为复杂，特别是当数据量较大时。

适用场景：

  • 金融市场数据（如股价、外汇、商品期货等的波动性建模）。

  • 风险管理（如Value at Risk，VaR 计算）。

  • 宏观经济变量的波动性建模。

核心案例

使用虚拟的股市收益率数据，进行 GARCH 模型的建模和分析，绘制以下图：

  1. 条件方差（波动率）的变化趋势图。

  2. 股票收益率与条件方差的关系图。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from arch import arch_model
from statsmodels.tsa.stattools import adfuller

# 生成虚拟股市数据（随机游走模型）
np.random.seed(42)
n = 1000
returns = np.random.randn(n)  # 正态分布的收益率数据
price = 100 + np.cumsum(returns)  # 模拟股票价格
time_series = pd.Series(price, name="Stock Price")

# 计算收益率
stock_returns = np.diff(np.log(time_series)) * 100  # 对数收益率（百分比）
stock_returns = pd.Series(stock_returns, index=time_series.index[1:], name="Stock Returns")

# 绘制收益率的时间序列图
plt.figure(figsize=(12, 6))
plt.plot(stock_returns, label="Stock Returns", color="blue")
plt.title("Stock Returns Time Series", fontsize=14)
plt.legend()
plt.show()

# 检验收益率序列是否平稳（ADF检验）
adf_result = adfuller(stock_returns.dropna())
print(f"ADF Statistic: {adf_result[0]}")
print(f"p-value: {adf_result[1]}")

# GARCH(1, 1) 模型拟合
model = arch_model(stock_returns, vol='Garch', p=1, q=1)
model_fit = model.fit()

# 获取拟合的条件方差
conditional_volatility = model_fit.conditional_volatility

# 绘制条件方差（波动率）的变化趋势
plt.figure(figsize=(12, 6))
plt.plot(conditional_volatility, label="Conditional Volatility (GARCH)", color="red")
plt.title("Conditional Volatility over Time", fontsize=14)
plt.legend()
plt.show()

# 绘制收益率与条件方差的关系
plt.figure(figsize=(12, 6))
plt.scatter(stock_returns, conditional_volatility, color="green", alpha=0.5)
plt.title("Stock Returns vs Conditional Volatility", fontsize=14)
plt.xlabel("Stock Returns")
plt.ylabel("Conditional Volatility")
plt.show()

# EGARCH 模型拟合
egarch_model = arch_model(stock_returns, vol='EGarch', p=1, q=1)
egarch_fit = egarch_model.fit()

# 获取拟合的条件方差
egarch_conditional_volatility = egarch_fit.conditional_volatility

# 绘制EGARCH模型的条件方差
plt.figure(figsize=(12, 6))
plt.plot(egarch_conditional_volatility, label="Conditional Volatility (EGARCH)", color="purple")
plt.title("Conditional Volatility over Time (EGARCH)", fontsize=14)
plt.legend()
plt.show()

# TGARCH 模型拟合
tgarch_model = arch_model(stock_returns, vol='Garch', p=1, q=1, dist='t')
tgarch_fit = tgarch_model.fit()

# 获取拟合的条件方差
tgarch_conditional_volatility = tgarch_fit.conditional_volatility

# 绘制TGARCH模型的条件方差
plt.figure(figsize=(12, 6))
plt.plot(tgarch_conditional_volatility, label="Conditional Volatility (TGARCH)", color="orange")
plt.title("Conditional Volatility over Time (TGARCH)", fontsize=14)
plt.legend()
plt.show()

  1. 条件方差（波动率）的变化趋势图：通过 GARCH、EGARCH 和 TGARCH 模型计算出的条件方差图，展示了收益率波动性随时间的变化。在市场动荡时期，波动性通常较大，而在平稳时期，波动性较低。

  2. 收益率与条件方差的关系图：绘制股票收益率与对应条件方差之间的散点图。可以看到，极端的收益率（如大幅上涨或下跌）通常伴随较高的条件方差，表示市场波动加剧。

广义条件异方差模型（如 GARCH、EGARCH 和 TGARCH）在处理金融数据时非常有效，能够捕捉波动性聚集现象和非对称效应。

9. 长短期记忆网络

原理和核心公式

LSTM（长短期记忆网络）是一种特殊的循环神经网络（RNN），通过引入“门控”机制来解决标准RNN在学习长时间依赖关系时的梯度消失问题。LSTM通过以下几个门来控制信息流：

  • 遗忘门：决定保留多少历史信息。

  • 输入门：决定当前时刻的新信息有多少被加入到细胞状态中。

  • 输出门：决定下一时刻的输出。

LSTM的公式如下：

  • 遗忘门：

  • 输入门：

  • 候选记忆单元：

  • 更新细胞状态：

  • 输出门：

  • 最终输出：

这些公式描述了LSTM如何处理和更新状态信息，并最终生成预测。

优缺点和适用场景

优点：

  • 解决了标准 RNN 在长序列中的梯度消失问题。

  • 能够记住长期依赖信息，适合时间序列预测。

  • 可以处理不同长度的序列数据。

缺点：

  • 相对于传统的机器学习方法，LSTM模型训练较慢，需要更多的计算资源。

  • 模型复杂，需要调整的超参数较多。

适用场景：

  • 股票预测、气象预测、文本生成、语音识别、自然语言处理。

核心案例

下面是使用 PyTorch 实现 LSTM 来进行股票价格预测的代码。我们会使用虚拟数据，模拟股市价格，并通过 LSTM 模型进行预测。

import torch
import torch.nn as nn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split

# 生成虚拟股市数据
np.random.seed(42)
n = 1000
returns = np.random.randn(n)  # 正态分布的收益率数据
price = 100 + np.cumsum(returns)  # 模拟股票价格
time_series = pd.Series(price, name="Stock Price")

# 规范化数据到 [0, 1] 范围
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_data = scaler.fit_transform(time_series.values.reshape(-1, 1))

# 创建数据集，用于LSTM模型
def create_dataset(data, time_step=1):
    X, y = [], []
    for i in range(len(data)-time_step-1):
        X.append(data[i:(i+time_step), 0])
        y.append(data[i + time_step, 0])
    return np.array(X), np.array(y)

# 定义时间步长
time_step = 60

# 创建数据集
X, y = create_dataset(scaled_data, time_step)

# 训练集和测试集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False)

# 数据重塑为 LSTM 输入格式 [samples, time steps, features]
X_train = X_train.reshape(X_train.shape[0], X_train.shape[1], 1)
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1], 1)

# 转换为 PyTorch 张量
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32).view(-1, 1)
y_test = torch.tensor(y_test, dtype=torch.float32).view(-1, 1)

# LSTM模型定义
class LSTMModel(nn.Module):
    def __init__(self, input_size, hidden_layer_size, output_size):
        super(LSTMModel, self).__init__()
        self.hidden_layer_size = hidden_layer_size
        self.lstm = nn.LSTM(input_size, hidden_layer_size)
        self.linear = nn.Linear(hidden_layer_size, output_size)

    def forward(self, input_seq):
        lstm_out, _ = self.lstm(input_seq)
        predictions = self.linear(lstm_out[:, -1])
        return predictions

# 模型实例化
input_size = 1  # 输入特征的数量
hidden_layer_size = 64  # 隐层单元数量
output_size = 1  # 输出为1，表示股价预测

model = LSTMModel(input_size, hidden_layer_size, output_size)

# 损失函数和优化器
loss_function = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

# 训练模型
epochs = 50
for epoch in range(epochs):
    model.train()
    optimizer.zero_grad()

    # 前向传播
    y_pred = model(X_train)

    # 计算损失
    single_loss = loss_function(y_pred, y_train)

    # 反向传播
    single_loss.backward()
    optimizer.step()

    if (epoch + 1) % 10 == 0:
        print(f"Epoch {epoch+1}/{epochs}, Loss: {single_loss.item()}")

# 测试模型
model.eval()
with torch.no_grad():
    train_predict = model(X_train)
    test_predict = model(X_test)

# 逆规范化数据
train_predict = scaler.inverse_transform(train_predict.numpy())
y_train_actual = scaler.inverse_transform(y_train.numpy())
test_predict = scaler.inverse_transform(test_predict.numpy())
y_test_actual = scaler.inverse_transform(y_test.numpy())

# 修正实际测试数据的范围
actual_test_prices = time_series.values[len(y_train_actual) + time_step: len(y_train_actual) + time_step + len(test_predict)]

# 绘制测试数据与预测数据的比较图
plt.figure(figsize=(14, 6))

# 实际测试数据
plt.plot(actual_test_prices, color="blue", label="Actual Price (Test)")

# 预测数据
plt.plot(test_predict.flatten(), color="red", label="Predicted Price (Test)")

plt.title("Stock Price Prediction (Test Set)", fontsize=14)
plt.legend()
plt.show()

训练数据与预测数据的比较图：该图展示了模型在训练集上的预测效果。红色线表示LSTM模型在训练集上的预测股价，而蓝色线表示实际的训练股价。通过观察这两条线的重合度，可以评估模型在训练数据上的表现。

测试数据与预测数据的比较图：该图展示了LSTM模型在测试集上的预测效果。红色线表示模型预测的股价，而蓝色线表示实际的股价。测试集中的数据通常会更具挑战性，模型的预测效果有助于评估其泛化能力。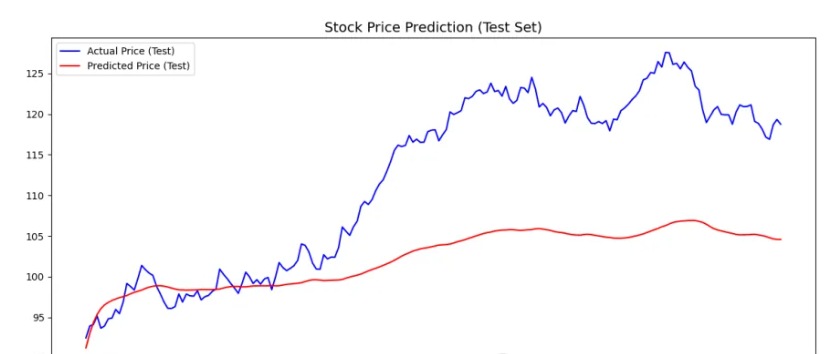

LSTM 模型能够有效地处理时间序列数据，尤其适用于具有长期依赖关系的数据。

10. Prophet模型

Prophet 模型

Prophet 是由 Facebook 开发的时间序列预测模型，旨在对具有强季节性（如日、周、年周期）和节假日效应的时间序列数据进行预测。该模型的主要优点是其自动化和易于使用，适用于具有复杂趋势和季节性的数据。Prophet 通过加法模型来表示时间序列，其中包括趋势部分、季节性部分和假期效应部分。

原理

Prophet 模型的主要思想是将时间序列分解成以下几个部分：

  • 趋势部分：可以是线性或对数的增长趋势，表示数据的长期变化。

  • 季节性部分：周期性波动，通常分为年季节性、月季节性、周季节性等。

  • 节假日效应：考虑到节假日等特定日期的异常波动。

Prophet 模型的基本结构如下：

其中：

  •  是在时间点  的观测值。

  •  是趋势部分，通常是线性或对数函数。

  •  是季节性部分，捕捉周期性波动。

  •  是节假日效应部分。

  •  是误差项。

趋势部分：

Prophet 的趋势是分段的，可以是线性或对数增长，通常使用分段线性回归模型。

季节性部分：

季节性部分通过傅里叶级数来表示，允许复杂的季节性波动。

假期效应：

通过用户输入的假期列表，模型能够对节假日的异常波动进行建模。

核心公式

Prophet 模型使用加法模型表示时间序列：

  •  是趋势部分，使用分段线性函数或对数函数表示。

  •  是季节性部分，使用傅里叶级数表示季节性波动。

  •  是节假日效应，通过设定的节假日列表来调整。

趋势建模

  • 对于线性趋势，公式为：

  • 对于对数趋势，公式为：

季节性建模

季节性部分是通过傅里叶级数表示的：

其中  是周期， 和  是傅里叶系数。

假期建模

假期影响通过在模型中加入假期效应进行建模，假期效应  被模型自动学习。

优缺点和适用场景

优点：

  • 容易使用，适合非专家进行时间序列预测。

  • 能够处理季节性、趋势和节假日效应。

  • 自动选择最适合数据的趋势类型（线性或对数）。

  • 可以处理缺失数据，且对异常值具有鲁棒性。

缺点：

  • 不适用于具有复杂动态依赖的时间序列（如金融市场数据）。

  • 对季节性变化的周期性要求较强，对于不规则的时间序列数据效果较差。

适用场景：

  • 销售预测、电力需求预测、流量预测等。

  • 适用于有明显季节性和趋势的数据。

  • 可以用于节假日效应建模，如电商促销活动的影响。

核心案例

以下是使用 Prophet 模型进行时间序列预测的 Pyhton 代码示例。我们使用虚拟的销售数据来展示 Prophet 的使用。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from fbprophet import Prophet

# 生成虚拟数据（例如，某商品的销售数据）
np.random.seed(42)
days = pd.date_range(start='2020-01-01', periods=500, freq='D')
sales = 50 + np.sin(np.linspace(0, 10, 500)) * 10 + np.random.randn(500) * 5
data = pd.DataFrame({'ds': days, 'y': sales})

# 可视化数据
plt.figure(figsize=(10, 6))
plt.plot(data['ds'], data['y'], label='Actual Sales', color='blue')
plt.title("Sales Data (Actual)", fontsize=14)
plt.xlabel('Date')
plt.ylabel('Sales')
plt.legend()
plt.show()

# 初始化 Prophet 模型
model = Prophet()

# 拟合数据
model.fit(data)

# 创建未来数据框
future = model.make_future_dataframe(data, periods=60)

# 进行预测
forecast = model.predict(future)

# 可视化预测结果
plt.figure(figsize=(10, 6))
model.plot(forecast)
plt.title("Sales Prediction with Prophet", fontsize=14)
plt.xlabel('Date')
plt.ylabel('Sales')
plt.show()

# 可视化预测的组件
plt.figure(figsize=(10, 6))
model.plot_components(forecast)
plt.title("Sales Prediction Components", fontsize=14)
plt.show()

  1. 实际销售数据：第一个图展示了原始的销售数据，我们通过合成的数据生成了一个包含季节性波动和随机噪声的销售序列。这张图主要用来直观地观察数据的变化趋势。

  2. 销售预测图：第二个图展示了通过 Prophet 模型进行预测后的结果。红色的区域表示预测的区间，黑色的线表示实际数据，蓝色的线表示模型的预测结果。这张图展示了模型如何从历史数据预测未来的销售趋势。

  3. 预测组件：第三个图展示了模型预测的组成部分，包括趋势（Trend）、季节性（Yearly）和假期效应（如果有的话）。这些组件帮助我们理解模型如何分解时间序列并识别趋势和季节性波动。

Prophet 是一个非常强大的时间序列预测工具，适用于具有季节性和趋势的时间序列数据。它具有易用性强、鲁棒性好、自动化程度高等优点，非常适合用于销售预测、流量预测、电力需求预测等场景。

最后

大家有问题可以直接在评论区留言即可~

喜欢本文的朋友可以收藏、点赞、转发起来！

第一个！时间序列大模型！
强化学习曾小健
04-13 3061
TimeGPT是Nixtla公司研发的一个用于预测任务的智能模型。这个模型采用了生成式预训练Transformer技术，有自我关注机制和局部位置编码。它由很多层的编码器和解码器组成，每个部分都有残差连接和层归一化，使得预测更准确。TimeGPT这个模型很强大，它可以处理不同频率和特征的时间序列，也能适应不同大小的输入和预测范围。最厉害的是，它只需要用历史数据作为输入，不用再次训练，就能对新的时间序列进行准确的预测。
Algorithm：【算法进阶之路】之算法面试刷题集合—数据结构的简介、最强学习路线(逻辑结构【数组-链表-栈和队列/树-图-哈希】、物理结构【元素/关系】、数据运算【十大排序/四大查找-图三大搜索-
头部AI社区如有邀博主AI主题演讲请私信—心比天高，仗剑走天涯，保持热爱，奔赴向梦想！低调，专注，谦虚，自律，反思，成长，还算比较正能量的博主，公益免费传播…内心特别想在AI界做出一些可以推进历史进程影响力的技术(兴趣使然，有点小情怀，也有点使命感呀
08-05 6215
​ Algorithm：【算法进阶之路】之算法面试刷题集合—数据结构的简介、最强学习路线(逻辑结构【数组-链表-栈和队列/树-图-哈希】、物理结构【元素/关系】、数据运算【十大排序/四大查找-图三大搜索-树三大遍历】、高级算法【枚举/回溯/递归/分治/动规/贪心】)、问题为导向的十大类刷题算法总结之详细攻略 目录 相关文章 数据结构思维导图 基本术语 一、数据结构的概述 二、数据的逻辑结构 三、数据的物理结构 四、数据的运算
通透！十大时间序列模型 最强总结 ！！
最新发布
xx_nm98的博客
09-11 7845
通过分析历史数据，这些模型揭示了潜在的模式和季节性变化，从而提供了数据驱动的预测。有效的时间序列预测还能够提高供应链管理、市场策略和风险控制的精确性。为此，咱们今儿和大家聊的十种最常见的时间序列模型有：自回归移动平均模型（ARMA）自回归积分滑动平均模型（ARIMA）季节性自回归积分滑动平均模型（SARIMA）向量自回归模型（VAR）广义自回归条件异方差模型（GARCH）Prophet长短期记忆网络（LSTM）门控循环单元（GRU）贝叶斯结构时间序列模型（BSTS）
时间序列（一）：时间序列数据与时间序列预测模型
Smilecoc的博客
01-30 13万+
时间序列定义： 时间序列是按照一定的时间间隔排列的一组数据，其时间间隔可以是任意的时间单位，如小时、日、周月等。比如，每天某产品的用户数量，每个月的销售额，这些数据形成了以一定时间间隔的数据。 通过对这些时间序列的分析，从中发现和揭示现象发展变化的规律，并将这些知识和信息用于预测。比如销售量是上升还是下降，销售量是否与季节有关，是否可以通过现有的数据预测未来一年的销售额是多少等。 对于时间序列的预测，由于很难确定它与其他变量之间的关系，这时我们就不能用回归去预测，而应使用时间序列方法进行预测。 采用时间序列
时间序列大模型：TimeGPT
weixin_43564920的博客
01-23 2492
基础模型在时间序列预测任务中的潜力仍然未被充分探索，但有迹象表明可以在不降低性能的情况下将预训练模型转移到不同任务上，且在时间序列预测任务中存在数据和模型规模的扩展律。TimeGPT 是一种由 Nixtla 开发的专门用于预测任务的生成式预训练 Transformer 模型，具有自我关注机制，采用历史值窗口生成预测，添加局部位置编码，由多层编码器-解码器结构组成，每个结构都具有残差连接和层归一化。在处理新时间序列推理问题时，我们采用滚动预测的方法来估计模型预测特定目标时间序列的误差，以确保预测的准确性。
时间序列模型
qq_55041016的博客
07-05 4446
时间序列算法总结...更新中
理工学---算法模型---时间序列模型
01-16 8万+
1、时间序列时间序列是时间间隔不变的情况下收集的不同时间点数据集合，这些集合被分析用来了解长期发展趋势及为了预测未来。 时间序列与常见的回归问题的不同点在于: 1、时间序列是跟时间有关的;而线性回归模型的假设：观察结果是独立的在这种情况下是不成立的。 2、随着上升或者下降的趋势，更多的时间序列出现季节性趋势的形式；常用的时间序列模型有AR模型、MA模型、ARMA模型和ARIMA模型等。2、时间
数据简化社区2018年全球数据库总结及18种主流数据库介绍(公号回复“数据库2018”下载典藏版PDF报告)
数据简化DataSimp社区
08-16 9540
数据简化社区2018年全球数据库总结及18种主流数据库介绍(公号回复“数据库2018”下载典藏版PDF报告) 秦陇纪 数据简化DataSimp 今天 数据简化DataSimp导读：Google搜索量最大的DB-Engines数据库排名，介绍前几名数据库特点、云AI区块链等数据库服务；展望2018年数据库发展趋势，本文合计40k字详读约需36分钟。最近群里说国内可以重新使用谷歌搜索、谷歌学术...
ADAS技术市场总结展望（2021年-2022年）
吴建明wujianming_110117
01-18 8360
ADAS技术市场总结展望（2021年-2022年） NV AGX 和TI的TDA4平台哪个好？ 作为自动驾驶的平台，NV好像用的人比较多，但TI的TDA4看起来也是不错的东西，有高手能够做个对比分析么？ 从CPU架构及主频来看，TDA4 介于 NV AGX的 Xavier 及 Orin 之间；但算力肯定比不上精于GPU的英伟达，毕竟 TI 是比较擅长的是 DSP 领域。 再从社区及厂商采用度来看，NV AGX明显要占优势。国内的三大新能源企业都用的是NV AGX：小鹏P7（Xavier），理想 One （
AIGC内容分享(二)：全球大模型技术与应用分析
之乎者也·的博客
01-09 1876
这篇文章主要阅读者是产品经理、业务负责人、AIGC核心参与者等。现在AIGC技术发展太快，每天都有不同的变化。刚才我看Google发布的Gemini多模态能力，着实被惊喜（吓）到了：AI可以看图说话、理解和推理、预测事情的发展动态，简直无所不能。所以这篇文章是想站在2023年底这个节点，系统性梳理下AIGC的技术现状和行业应用，方便我们对AIGC技术、产品和商业有个全局的理解。警示: 不论行业热度如何，企业AIGC布局始终需要保持理性和克制。
精通MATLAB回归分析：从入门到精通的十大数据挖掘案例
回归分析是统计学中应用最广泛的技术之一，它通过研究两个或多个变量间的统计关系，建立数学模型来预测或评估变量间的关系。MATLAB（Matrix Laboratory的缩写）是一款高性能数值计算环境，它提供了丰富的函数库，...
时间序列的7种预测模型
热门推荐
rosefun96的博客
12-23 19万+
背景 时间序列问题比较常见，比如股市，工业生产指标等。 1 朴素估计 使用最后一个时间点的值估测后面一段时间段的值。 2 简单平均 4 滑动窗平均 使用之前一定大小时间段的平均值作为这个时间点的值。 或者使用加权的滑动窗平均： y_hat_avg = test.copy() y_hat_avg['moving_avg_forecast'] = train['Count'].rollin...
十大时间序列模型最强总结（三）季节性自回归积分滑动平均模型（SARIMA）
老皮的博客
08-28 1591
AI大模型作为人工智能领域的重要技术突破，正成为推动各行各业创新和转型的关键力量。抓住AI大模型的风口，掌握AI大模型的知识和技能将变得越来越重要。学习AI大模型是一个系统的过程，需要从基础开始，逐步深入到更高级的技术。这里给大家精心整理了一份全面的AI大模型学习资源，包括：AI大模型全套学习路线图（从入门到实战）、精品AI大模型学习书籍手册、视频教程、实战学习、面试题等，资料免费分享！
常见时间序列模型
Coix的专栏
12-30 1万+
本文主要对各种时间序列模型及其特征做了一个归纳总结，以便查询了解。 符号说明： 变量： x,yx,yx,y 变量集：X,YX,YX,Y 变量xxx在ttt时刻的值：xtx_txt​ 参数：α,β\alpha, \betaα,β ##自回归模型（Autoregressive model，AR） 自回归，顾名思义，就是用自己预测自己，即用同一变量xxx之前的信息{x1,x2,…,xt−1}\{x_1,...
4大类11种常见的时间序列预测方法总结和代码示例
deephub
02-26 4万+
本篇文章将总结时间序列预测方法，并将所有方法分类介绍并提供相应的python代码示例，以下是本文将要介绍的方法列表： 1、使用平滑技术进行时间序列预测 指数平滑 Holt-Winters 法 2、单变量时间序列预测 自回归 (AR) 移动平均模型 (MA) 自回归滑动平均模型 (ARMA) 差分整合移动平均自回归模型 (ARIMA) 季节性 ARIMA (SARIMA) 3、外生变量的时间序列预测 包含外生变量的SARIMAX (SARIMAX) 具有外生回归量的向量自回归移动平均 (VARMA
时间序列常用模型
aipotong0564的博客
05-15 6532
1、自回归模型（英语：Autoregressive model，简称AR模型），是统计上一种处理时间序列的方法。 或者也可为 其中： c是常数项；被假设为平均数等于0，标准差等于的随机误差值；被假设为对于任何的t都不变。 文字叙述为：X的当期值等于一个或数个落后期的线性组合，加常数项，加随机误差。 2、MA(Moving Average...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值