概率论考点之指数分布，泊松分布及积分（一维随机变量内容）

因为做项目的原因，不能集中精力去复习，还是发现概率论有难度，可能是高数学的太差了吧！到10月17日考试，剩58天，估计是有些困难的，先不备考概率论了，临时转向备考数据库。留出空余的时间来复习高数。和软考！不能让自己懈怠，多线作战的目的就是养成学习的习惯！

今天得知8月自考，马原，近史、网络。都已经通过了！虽然网络只考了66分，以后要拿学位的话，还要补考一次。但这些都是后话了。还是挺高兴的。

                                                                                                                             --------2020年8月20日

此贴，待10月份自考结束后，再继续备考概率论。

如题:2019年10月

分析:10月17日，考完数据库后，补充

答案：详见：第九个问题：看到指数分布想到啥？？？？？

 

想到的第一个问题是：X是离散型随机变量还是连续型随机变量呢？两者又有什么区别呢？

可以这么简单的理解：坐标轴上的点，就是离散型的，而坐标轴上的面（或者叫区间），就是连续型的。随机变量就是实验结果值。

第二个问题，想到的是e是什么？高数的东西忘的差不多了

函数f(x)=(1+1/x)^x，当x趋向于无穷大时，可以证明此函数有极限，且极限是一无理数，于是就把这一极限值记为e，作为自然对数的底，约为2.718281828
e在物理、化学、生物等基础科学以及工程技术方面都非常有用，因为自然界的很多现象都跟它息息相关。

第三个问题，分布律和分布函数有什么区别呢？

分布律是对应离散随机变量、分布函数对应连续随机变量,意义是小于等于该点的所有情况的概率,对方差或者期望的计算公式使用起来比较方便.

分布函数是对应一个面上面概率的取值（极端的理解：就是布满整个空间，再用分布律就没法表示了）,对于离散型随机变量来说，其实是一个累计概率，所以是比较适合统计的。连续型随机变量更是如此。分布函数，比较通俗的理解就是不大于某个值的概率，如次品不大于5个的概率。

而分布律，可以理解为数据库中的关系表，就是一个key值，对应一个概率值

第四个问题：分布函数性质如何理解来？？

分布函数F ( x ) 表示随机变量取值小于或等于x的概率,是一个区间的概率。很具有实用意义。如次品率不大于某个值是人们所关心的，而不是次品率为某个值，这也证实了一个真理，世上没有绝对的事，只不过是概率大小而矣。

性质：1、0<=F(x)<=1,好理解，分布函数也是概率值，肯定会是这个范围内。

2、x1<x2,那么F(x1)<=F(x2),这就是不减性。一定要转过这个弯来。单纯从F(x1)<=F(x2)来看就是随机变量落在小于等于x1上的区间的概率 < 落在小于等于x2上的区间的概率。为什么？

涉及到分布函数，就将坐标轴上点的值转成了区间的关系了，此时的x1还没真正上升到空间这层关系，只是坐标上的一个点（极端认为就是X轴上的一个点），x2是坐标轴上一个大于x1的点，那么显然两个区间是存在包含关系的。用概率论语言来说就是x1区间发生概率一定会导致x2区间的值发生。因此F(x1)的概率一定是小于F(x2)的概率。

证明，是取了x1与x2中间的一个点为随机变量，再转化成离散随机变量分布律（即点的值，当前来说还只是轴上的值），将坐标轴上值转成区间（也就是分布函数）即可推导出来。

3、F(+∞)=1,F(-∞)=0,好记，概率性质。

4、这个也好理解，轴上右边的数越接近点值时，肯定就越接近点值概率。

分布函数在概率论中的意义：其实就是求区间的概率，都可由F(x)概率得出。

第五个问题：题目所说的指数函数是离散型的还是连续型的随机变量呢？？？？为什么呢？

首先说下，连续型随机变量包含的意义：

连续型随机变量是在某个区间内连续取值（轴上取值+曲线边也就是面），并且可以认为其取得某个具体数值的概率为 0（因为面内的点有很多，所以取到具到点的值，概率极小）。正因为如此，在讨论连续型随机变量的概率分布时，我们更关心的是它在某一个区间上的概率密度函数 Probability Density Function，依然用 ƒ(x) 表示，这个函数在某个区间上的积分则对应随机变量的取值落在这个区间的概率。

换句话说，分布函数指的是积分，而概率密度指的是曲线（也就是导数，代表趋势）。

实质上连续型随机变量的分布函数，还是分布函数的定义，只不过是用积分来表示的。

指数型，想想它在坐标轴中的图形就知道是连续型，因为位于坐标轴所夹的中间，一定不会是坐标轴上的点，而是曲线。

第六个问题上面说了积分，什么是微分来？什么是导数来？

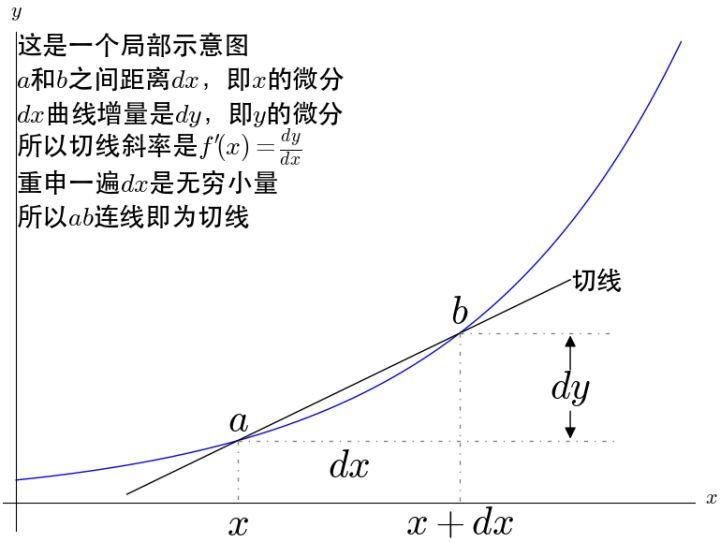
 从这张图得出导数的定义       而dx 和 dy被称为  x和 y 的微分，都为无穷小量，所以导数也被莱布尼兹称为微商（微分之商)。         

用极限的思想来定义导数，其实是和无穷小量一回事，只不过更严谨。因为极限是靠近参照系（靠近X轴）。现代微积分中微分，正是由极限推出导数，再由导数定义的微分。

如下图：

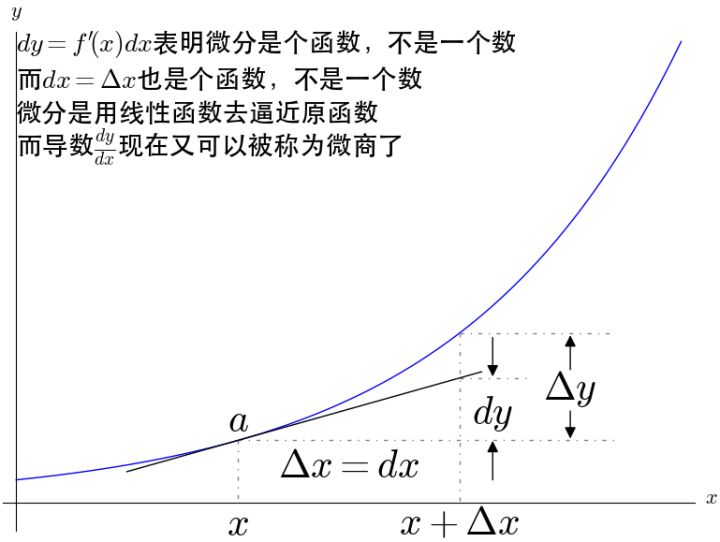
由以上，可以看到，导数意义就是曲线的点的切线，描绘的是曲线的趋势。

而微分描述是面积，并且是极小量的面积

微分的面积之和，其实就是积分。

积分与导数关系密切，因为积分就是导数所代表的曲线与X轴上的点围成的。

第七个问题：如何求积分来？

可以套公式，但太多，是记不住的，还得从原理上理解，另外多做些题。

定积分的结果是一个确定的值。代入不定积分的反导函数得来。

不定积分的结果还是一个函数，就是反导函数，什么是反导函数呢？可以理解为导数公式的左边的部分。如导数（曲线的切线）公式(x^2)'=2x，那么x^2就是反导函数（也就是曲线）。

反导函数狭义理解就是积分表达式，更直白的说，反导就是积分。

以上其实是自己复习的高等数学的一些内容，跟本文主题指数分布有些偏离。费了好几天的功夫，呵。

第八个问题：均匀分布的本质是什么?这几天还是看书，好好理解书上的概念。除正态分布外，次重要的内容。

均匀概率分布是古典概率分布的连续形式，是指随机事件的可能结果是连续型数据变量，所有的连续型数据结果所对应的概率相等。回顾古典概率分布，如图2-17所示，掷骰子点数结果的概率分布就是一个典型的古典概率分布，投掷的点数结果是六个离散型数值(1,2,3,4,5,6)，它们的发生概率相等，都是1/6。如果将离散型数据结果(1,2,3,4,5,6)换成连续型数据结果的取值区域(1<=x<=6)，并且所有的连续型数据结果的发生概率相等，依旧等于1/6，则离散型的古典概率分布就转换成为连续型的均匀概率分布。如下图所示：

均匀概率分布的概率密度函数为：

从概率密度定义也可以看出，均匀分布只与区间[a,b]有关。为什么？

因为概率密度其实是指曲线的趋势，均匀分布的曲线是一条平行于x轴的直线。x轴代表就是区间。x轴与y轴间曲线代表导数表达式（也就是概率密度），反导也就是积分表达式（分布函数）。可见只要知道曲线（概率密度）就可以求出积分（分布函数），所以学概率论导数（曲线）的公式还是必须要记住的。尤其是以下这个：

以上其实是由概率密度推导分布函数的过程：其实，也可以从图2-3中直接推出面积从而得到分布函数的公式，F(x)代表X<=x的面积，不就是x-a吗，再乘以宽固定的这很重要，也是一种做题的方法，这样可以更准确，更快。能不算积分就不算积分。

 

由分布函数图像，为什么是一条斜线？因为积分是一个由x轴区间对应的y值累加的过程，肯定随着x值增加，y会不断成比例均匀增大，所以是一条斜线。这也就明白了，积分的曲线其实是不能表现出数据趋势的，本质上应该是导数（曲线）才能给出正确的趋势。并且，积分服从于导数。

从分布函数也可以得出，均匀分布概率规律

均匀概率分布，则落在区间内某个区间的概率只与这个区间的长度有关，而与该区间在区间内的位置无关。

第九个问题：看到指数分布想到啥？？？？？第三位的分布

这里的分布函数的推导：详见下图：

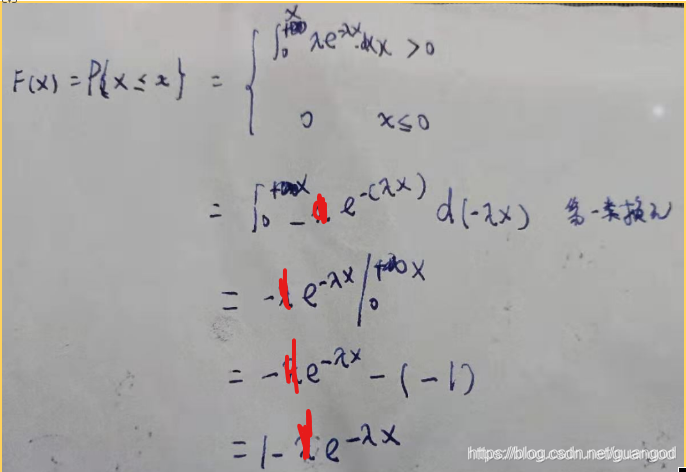
想到啥呢？泊松分布，还想到引题，正是考查的指数分布的分布函数定义。所以答案选B

• 泊松分布

首先，说下泊松分布，这个前段时间看过，但还是记不太清楚了，可见这块还是没有掌握。

基于过去某个随机事件在某段时间或某个空间内发生的平均次数，预测该随机事件在未来同样长的时间或同样大的空间内发生n次的概率。由于泊松分布适用于描述单位时间（或空间）内随机事件发生的次数，因此它常用于预测某些事件的发生，例如某家医院在一定时间内到达的人数；超市收银台在某段时间内的结账人数；公交车站在某个时间段的候车人数等。

 假定某个随机事件在过去的历史中，在固定长度时间段或固定大小空间内发生的平均次数为λ，那么就可以将固定长度的时间或固定大小的空间分成n等份；在每等份的时间或空间内，随机事件发生的概率可以表示为λ/n。若n趋向于无穷，也就是这段时间或空间被分成无数的小段，那么λ/n的值将趋近于0，也就是在每个等份的时间或空间内，该随机事件发生两次或两次以上是不可能的。根据以上假设条件，在固定长度时间或固定大小空间内，随机事件发生k次的概率服从二项概率分布，可以表示为：

K!与n^k互换就是左右互换一下。

注：

• 指数分布概率密度表达式

可以看到与泊松分布都有个e^-λ,从表达式上看两者就非常相似，到底有没有关系呢？

指数分布描述的是两次随机事件发生的时间间隔的概率分布情况，这里的时间间隔指的是一次随机事件发生到下一次随机事件再发生的时间间隔。放在二维坐标内理解，纵轴表示概率密度，横轴代表时间间隔长度，因为时间间隔长度可以取任意连续的数值，所以指数分布是一种连续型的概率分布。在现实生活中，指数分布的应用广泛。例如，某医院过去平均每10分钟出生一个婴儿，求接下来5分钟内有婴儿出生的概率；某公司的客服人员平均5分钟接一次电话，那么接下来2分钟内有电话打入的概率；某品牌的电脑平均10年出现一次重大事故，求该电脑5年内发生故障的概率等。

指数分布与泊松分布正好互补。泊松分布能够根据过去单位时间内随机事件的平均发生次数，推断未来相同的单位时间内随机事件发生不同次数的概率。而指数分布的作用是根据随机事件发生一次的平均等待时间来推断某个时间段内，随机事件发生的概率。

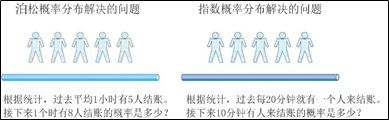
在管理科学中经常将两者结合起来共同解决排队理论等问题，如图2-14所示，泊松分布和指数分布可以帮助超市管理人员了解单位时间内结账顾客人数和空闲时间长度的概率分布，从而合理安排结账员的排班计划。

注意，使用指数分布进行概率计算时，一般平均等待时间u会大于假定时间x。下图是不同的指数分布概率密度曲线图，从图中可知，随机事件单位时间发生的次数越小，曲线越平缓，这是因为越小，表示随机事件发生一次需要等待的平均时间越长，随机事件可能发生在更长时间段内的任意一点，概率就被分散了。

离散型概率分布可以直接通过概率质量函数计算概率，而连续型分布则不能，需要通过对概率密度函数曲线下方的面积进行积分，积分面积才是所求的概率。指数分布的概率密度函数经过积分后得到概率计算公式为：

如下图所示，指数分布的概率是指数分布曲线下方的面积，面积被给定的时间长度x分为两部分。曲线下方的总面积等于1，表示随机事件在曲线覆盖的时间长度内（横轴表示时间长度）发生的概率是100%。

根据上图信息，可以对指数分布曲线做出描述：随机变量x 的取值范围是从0到无穷；曲线的极大值出现在x=0处，即f(0)=λ(单位时间内发生的次数）；曲线的长尾拖在右边，所以函数为右偏，随着给定时间长度的随机变量x的增大，曲线稳步下降。

指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间 t ，就等同于 t 之内没有任何婴儿出生。

反过来，事件在时间 t 之内发生的概率，就是1减去上面的值。

• 生活实例

电子成品因为它们不易坏的特性，所以保修期都比较长。某著名手机厂商生产的某型号手机平均10年才出现一次大的故障。为了制造销售热点，公司想将保修期提高到15年，但又不想增加过多的成本投入，所以需要考虑以下问题：① 该型号手机使用15年后还没有出现大故障的比例；② 如果厂家想提供大故障免费维修的质量担保，基于成本考虑，保修数量不能超过全部产量的20%，那么提供多长的保修年限最适宜。

分析思路

因为电子产品的耐用性，短期内发生两次大故障的概率非常小，案例需要分析的是不同时间段内发生大故障的手机比例，换个角度可以解释为不同时间段内该型号手机发生大故障的概率，可以用指数分布的概率公式计算概率。

该型号手机使用15年后还没有出现大故障的比例。已知该型号的手机平均10年发生一次大的故障，所以，单位时间(1年)内，发生故障的次数为 λ=1/10=0.1，代入指数分布的概率计算公式： 

从计算结果可知，该型号手机使用15年后没有发生大故障的概率是22.3%，换一种说法，就是只有22.3%的该型号手机在使用15年后没有发生大故障，而77.7%的手机都将在15年内进行维修，这个成本是极高的，远远超过20%的承受能力。厂家要求免费保修的比例不超过全部产量的20%，也就是要求在保修年限内发生大故障的手机比例不超过20%，可以列出不同保修年限对应的发生大故障手机的比例。

从表中可以看到：担保2年，需要维修的手机比例就达18.1%，担保3年，出现大故障的手机比例增加到25.9%，已经超过20%。所以，厂家应以2年为免费维修担保期。由此可见，如果厂家没有经过数据分析，盲目地推行15年的保修期承诺，将会给企业造成意想不到的沉重负担。

第十个问题：一维连续型随机变量最重要的分布：正态分布，考试的重点

1、概念：如下图：

三种连续型随机变量的分布都是由概率密度得到的概念，再由密度得到分布函数。

正态分布的分布函数：

2、什么是标准正态分布？？

标准正态分布的图形如下：

标准正态分布的性质：

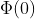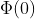（1）=1/2这个可以从标准正态分布的图形得到，因为是标准正态分布函数专用符号，所以表示小于0（-,0)的概率，占所有面积的一半，所以概率是1/2。

（2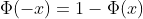）,也可由图形得到，隐含的计算逻辑是由于标准正态分布的图形是关于y轴对称的，所以任意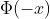即（-,-x)上的概率应该是与（x,)上的概率是相等的。如何表示（x,)上的概率呢？整体的概率减去（-,x)即,得到结论。

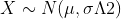  (3)，则Z=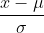 ~ N(0,1)，也就是对普通的正态分布而言，在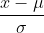处一定是符合标准正态分布的。这就为正态分布求法指出一条道路，也就是求正态分布，可以先将其标准化成标准正态分布。标准化之后，就是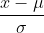处标准正态函数的值。计算时的思路如下：

1、一般是先找出u(均值）标准差(也就是正态分布给出的方差开根号

2、再将随机变量X(大x)与x两边同时减u,再除以西格马，换成符合标准正态分布形式

3、换成标准正态分布的随机变量就可以写成的形式，同时，小x也就符合的形式，因为小x一般是一个给出值，所以是有数值的，通过查正态分布表，就可以得到整体的正态分布的值。