三维重建----图像特征点检测与匹配

一、特征点检测

图像特征点介绍(基本是调用现成的库）

特征点的定义：检测子（给一副图像找到特征点的位置）+描述子（特征向量，用于特征匹配）

1.1 图像特征点应用

1）相机标定：棋盘格角点阴影格式固定，不同视角检测到点可以得到匹配结果，标定相机内参。

2）图像拼接：不同视角匹配恢复相机姿态

3）稠密重建：间接使用特征点作为种子点扩散匹配得到稠密点云

4）场景理解：词袋方法，特征点为中心生成关键词袋（关键特征）进行场景识别

1.2 图像特征点基本要求

  目前，衡量图像特征点的主要指标是重复性和差异性。

1）差异性（可检测）：特征点应该呈现出区别于非特征点的明显特征，比如灰度变化明显、边缘点等。

差异性示意图

2）重复性（可匹配）：对应同一三维点的特征点应该在不同视角中被重复检测到，如旋转、光度、尺度不变性。

重复性示意图

3）特征点有如下性质：

• 局部性：特征是局部的，对遮挡和混乱场景鲁棒
• 数量：一幅图像中可以产生足够数量的特征点，比如成百上千
• 独特性：可以和其他图像中大多数点相区分
• 高效：能够进行实时的检测和比较
• 可重复性：对图像进行旋转平移等操作后，仍能被检测到

特征点检测子

2.1 Harris角点检测方法**（早期，原理简单，视频跟踪，快速检测）**

在图像上选取的窗口

动机：特征点要具有局部差异性

以每个点为中心取一个窗口，例如，5×5/7×7的像素，描述特征点周围环境

此点具有差异性->窗口往任意方向移动，则周围环境变化较大->具有局部差异性

用数学语言来描述：

• 加和符号：表示窗口内每个像素
• w：表示权重，权值1或者以点为中心的高斯权重（离点越近权重越大）
• I：表示像素，彩色图像（RGB）/灰度图像（灰度）
• u，v：窗口移动的方向
• H：harris矩阵，由两个方向上的梯度构建而成
• 图像梯度：

Harris矩阵：

• Harris矩阵H 的特征值分解及分析
• 两个特征值反映相互垂直方向上的变化情况，分别代表变化最快和最慢的方向，特征值大变化快，特征值小变化慢
• SVD分解结果如下：

• λ1 ≈ λ2 ≈ 0， 两个方向上变化都很小，兴趣点位于光滑区域（例如白墙场景）
• λ1 > 0 , λ2 ≈ 0 ，一个方向变化快，一个方向变化慢，兴趣点位于边缘区域（图像的边缘位置）
• λ1 , λ2 > 0 ， 两个方向变化都很快，兴趣点位于角点区域（容易判断）（说明显著于区别周围的环境，正是我们想要的点）

即特征点检测工作就转换成了计算特征值大小的计算。

Harris角点准则代替矩阵分解：

• 反映特征值情况，trace为迹（矩阵分析知识点）
• k的值越小，检测子越敏感（K值越小，检测到的特征点就会越多）
• 只有当λ1和λ2同时取得最大值时，C才能取得较大值
• 避免了特征值分解，提高检测计算效率
• 非极大值抑制(Non-maximal Suppression) 选取局部响应最大值，避免重复的检测

  检测流程：一般先做滤波平滑，再求梯度，其目的是避免存在一些变化比较剧烈的一些值。

检测结果示例：

2.2 基于LoG的多尺度特征检测子

动机：Harris角点检测不具有尺度不变性（窗口尺寸选择困难），让特征点具有尺度不变性

• 解决方法：尺度归一化LoG算子，处理尺度的变化
• LoG算子：Lindeberg(1993)提出Laplacian of Gaussian (LoG)函数的极值点对应着特征点
• 尺度空间：

  一副图像使用不同大小滤波核滤波（例如：高斯滤波核），越大的滤波核越模糊，分辨率越小，不同滤波核滤波后的空间为尺度空间=3维空间（图像+尺度），模拟人类视觉，较远物体模糊，一系列滤波核构成的不同分辨率图像为尺度空间->LoG能够处理不同尺度的图像。（可以假设把图像叠起来，即构成一个3D空间）

LoG算子形式：高斯滤波性质：卷积->求拉普拉斯算子==求拉普拉斯算子->卷积 其中LoG算子如下：

由于不具备尺度可比性，因此需要做尺度归一化，实现统一比较。

尺度归一化LoG（使得具有可比性=汇率）：

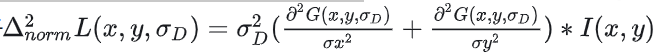其中尺度归一化LoG算子如下：

• 不同尺度下的LoG响应值不具有可比性

• 构建尺度空间，同时在位置空间和 尺度空间寻找归一化LoG极值(极大 /极小)点作为特征点

检测流程如下：

检测结果：效果好，但计算量较大。

2.3 基于DoG的特征检测子（SIFT）

实质就是对归一化的LoG做的近似。引入高斯空间的概念：

高斯差分DoG：相邻的空间做差，极点处对应特征点。

尺度空间的搭建（核心原理）：

高斯空间：

高斯差分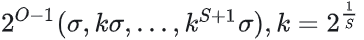：（DoG）

有效差分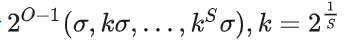：（尺度空间有上下两个邻域才可以，边界无效）

参数设置：

• 阶数： O=3 （octave=阶，每阶图像尺寸减少一半,阶数高->运算量大->尺度变化大）
• 每阶有效差分数：S=3（每个阶内划分数）
• 每阶层数：N=S+3（有效高斯差分图像）
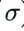• 为基本尺度，一般设置为1.6。

空间三维图如下所示：

一阶

二阶

三阶

• 特征点位置的确定：
• 1）尺度空间和图像空间上：3*3窗口，26个邻域，找极值点比其他都要大DoG，LoG找极大值或极小值
• 2）横轴向代表离散位置，纵轴代表DoG响应值，在极值点邻域内求二阶函数的极值=准确像素位置

在位置和尺度空间组成的三维空间中寻找极值点（离散空间的）。

如何获得亚像素的极值点？

计算方法如下：

x：代表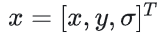，为三维，坐标空间+尺度空间。

f(x)：代表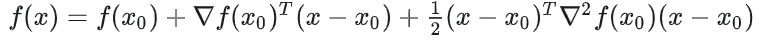为DoG值。

x0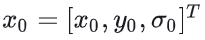： 检测到离散坐标下的极大值点（求极致点就是求导）。

在x0附近近似一个二阶函数，求二阶函数极值得到更准确的亚像素极值位置。
极值点有可能是边缘点，->除去边缘点：DoG在边缘处值较大，需要避免检测到边缘点

计算主方向：通过统计梯度直方图的方法确定主方向，使算法具有旋转不变性（相机或者图像发生旋转，依然可以检测到）

SIFT检测流程：旋转不变性、尺度不变性、亮度 变化不变性，对视角变化、仿射变换有一定程度的稳定性。

SIFT检测结果：

特征描述子（身份，匹配）

特征描述子的性质：

• 每个特征点独特的身份认证
• 同一空间点在不同视角的特征点具有高度相似的描述子（光度不变性）
• 不同特征点的描述子差异性尽量大
• 通常描述子是一个具有固定长度的向量（每一个点的特征）

特征支持区域：

• 主方向:进行旋转并重新插值
• 特征尺度:影响支持区域的大小

3.1 基于直方图的描述子

用于微小运动的描述子（相邻两帧视频）

• 定义：以特征点为中心的矩形区域内所有像素的灰度值作为描述子

特性：适用于微小变化的图像对 图像存在明显的旋转、尺度、光照和透视变换时不稳定

Sift描述子——旋转主方向（具有旋转不变性）

• 定义：根据主方向对支持区域进行旋转，并通过双线性插值重构。 （对支持区域内一定范围内的图像像素做梯度计算，即求导，确定该范围内图像的梯度方向，统计最多的方向为我们的主方向。）

• 特性：图像归一化处理，去除光照变化。（光照不变性）

旋转主方向

Sift描述子——统计局部梯度信息：

• 1）将区域划分成4x4的block ；
• 2）每个block内统计梯度方向 的直方图(高斯加权梯度作为系数)

Sift描述子——生成描述子：

Sift描述子——归一化处理：

• 处理方式
• 1）门限处理-直方图每个方向的梯度幅值不超过0.2
• 2）描述子长度归一化
• 特性：归一化处理提升了特征点光度变化的不变性
• SIFT描述子变种：PCA-SIFT/SURF

特征匹配

定义：计算两幅图像中特征描述子的匹配关系（特征点个数是不同的）

4.1 距离度量

归一化互相关，1 ->非常匹配，0->不匹配，用的最多的是欧式距离和归一化互相关（匹配）

4.2 匹配策略

最近邻：加了距离约束，防止孤立点，判断匹配是否可靠。

4.3 特征匹配验证

OpenCV里有现成的库ORB

单应性矩阵筛选更加可靠稳定

在同一平面上，效果所以更优

思考

深蓝学院课程-基于图像的三维重建视频学习笔记