关于三维空间中旋转矩阵的推导

0.上图形学的时候讲过这个东西的推导，但是记得很模糊，现在重新推导一下

1.问题描述

这里采用axis-angle表示，即：

计算围绕（x,y,z）向量旋转 α 角的旋转矩阵M（注：右手系）

2.基本思路

第一步，把向量（x,y,z）旋转到 Z 轴

第二步，绕此时的 Z 轴旋转α 角

第三步，把向量（x,y,z）旋转回去

3.计算

把上面三步的矩阵分别定义为A,B,C (M = C*B*A)

则可知A，C互为逆矩阵

B矩阵是简单的二维旋转的扩展，

B=

cosα    sinα    0

-sinα   cosα   0

0          0         1

由于把向量（x,y,z）旋转到 Z 轴又可以分为两步

第一步，把向量旋转到 XOZ 平面，矩阵R1

第二步，向量在 XOZ 平面上旋转，使向量与 Z 轴重合，矩阵R2

则：

A = R2 * R1

C =（R1 -1）*（R2 -1）

为了方便计算，定义向量（x,y,z）的分量分别为：

x = cosθ sinφ

y = sinθ sinφ

z = cosφ

（注，这样的定义是为了保证，上面的两次旋转的角度分别为θ ,φ）

然后，就可以得到：

R1=

 cosθ    sinθ   0

-sinθ    cosθ   0

 0           0        1

R2=

 cosφ    0       -sinφ

 0          1         0

sinφ      0        cosφ

最终要计算的三维旋转矩阵 M 就可以表示为：

M 

= C * B * A 

= (R1-1 * R2-1)  * B *  (R2 * R1)

把上面的矩阵代入上面的等式，就可以得到 M

此时得到的 M 是用 θ ,φ 表示的，把 θ ,φ表示回 x,y,z 就可以得到最终的 变换矩阵 M

4.最终结果：

（下面图片里的 θ，相当于上面叙述中的 α ）

图片来自： http://zh.wikipedia.org/wiki/%E6%97%8B%E8%BD%AC%E7%9F%A9%E9%98%B5 

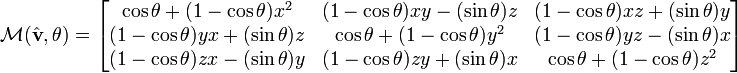
算了一下，虽然算起来很麻烦，但是结果还是对的 ：）