目录
基础知识
零极点
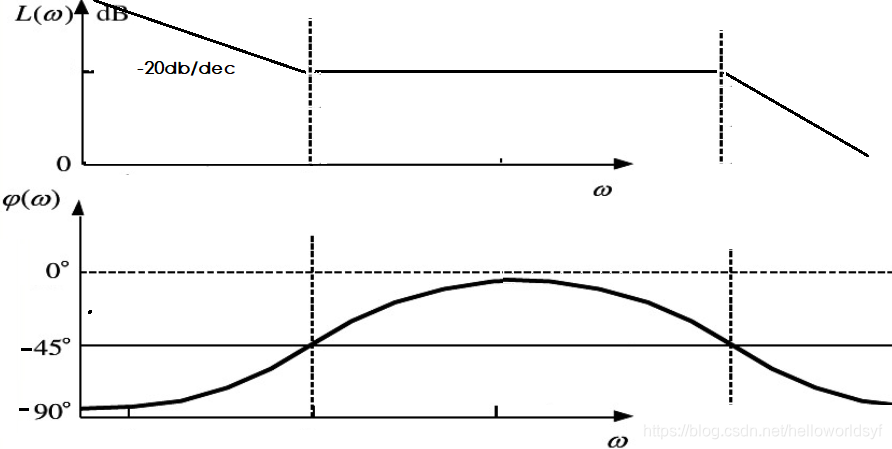
左半平面的极点 斜率-20db/dec增益;-90°相移
左半平面的零点 斜率20db/dec增益;90°相移
右半平面的零点 斜率20db/dec增益;-90°相移
右半平面的极点 不稳定系统
增益增加降低稳定性(比例环节大超调大);相位滞后降低了稳定性(就像交付延期)
所以极点和零点在左半平面 表现良好,极点和零点在右半平面可能不稳定,(极点右半平面发散,零点右半平面增加增益和相位滞后)
常见的几个环节
-
比例环节(比例器)
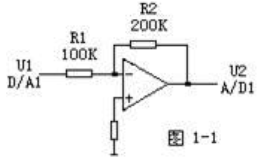

只影响变化的幅度,响应的速度,PID里面的P
-
积分环节(积分器)


能够降低高频增益减少高频噪声,降低稳态误差,但是会产生相位滞后降低响应速度和系统稳定性
-
惯性环节


-
一阶微分环节


环路的稳定
环路增益为1,相位滞后180°,系统不稳定发生自激振荡

开环与闭环
开环

输出滤波器
型滤波器
这个是BUCK拓扑适用,升压和升降压拓扑由于L不能剥离,需要稍微调整一下公式

这里忽略了一个输出电容的等效串联电阻(会带来零点)
阻尼系数因素决定了交接频率(谐振)的大小,系数越小输出越大(欠阻尼),
双极点会在谐振频率增益增加

功率级
-
反激变换器
其中
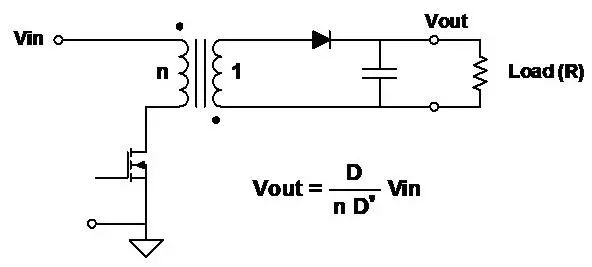 、
、
闭环
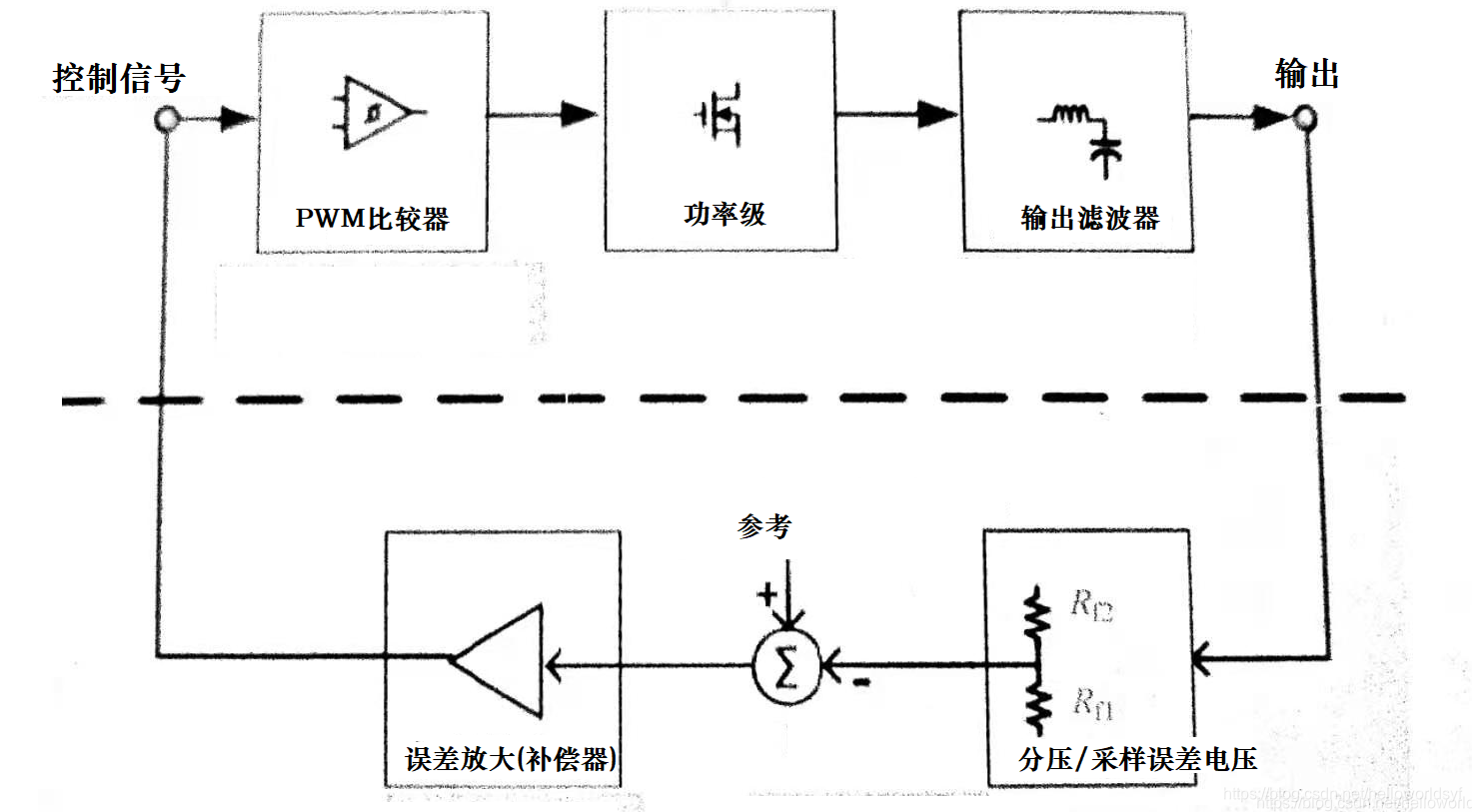

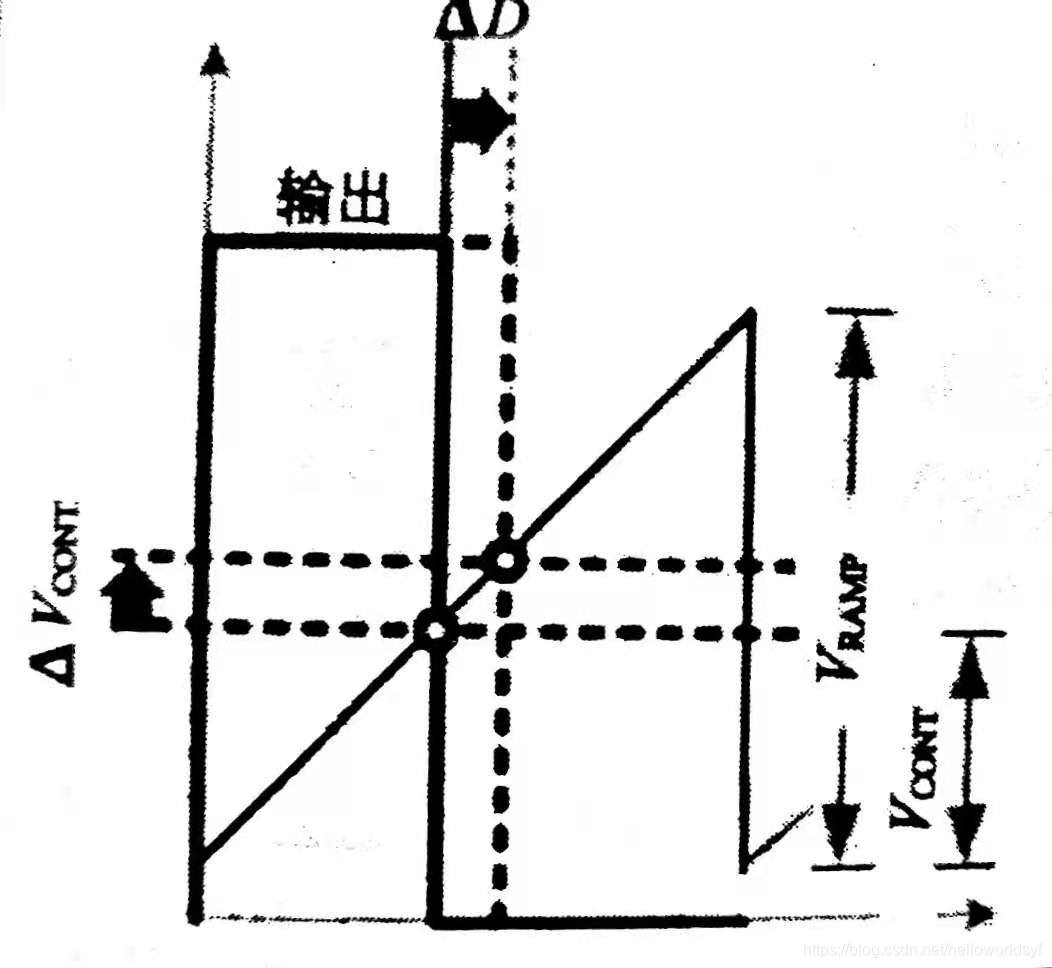
PWM比较器
Vout是控制电压,也就是误差放大(补偿器)的输出电压,VRamp是电流采样脚的斜波峰值电压

分压采样器
误差放大补偿器
下一节重点讲
反馈补偿
电压环
123型的补偿器电压环
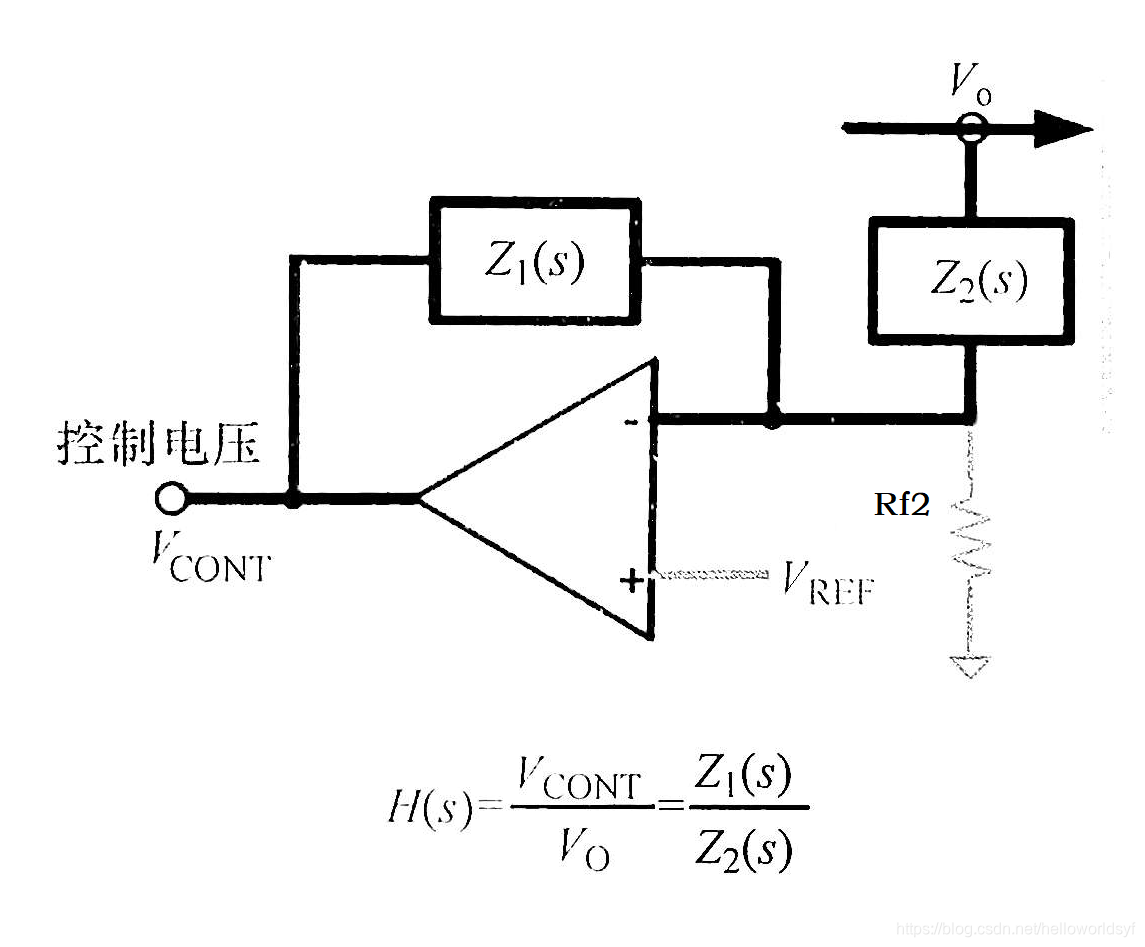
- PI调节器(II型补偿器)

因为运放虚地且输入接反相端,传递函数是 ;其中
;
;所以
431的电压环

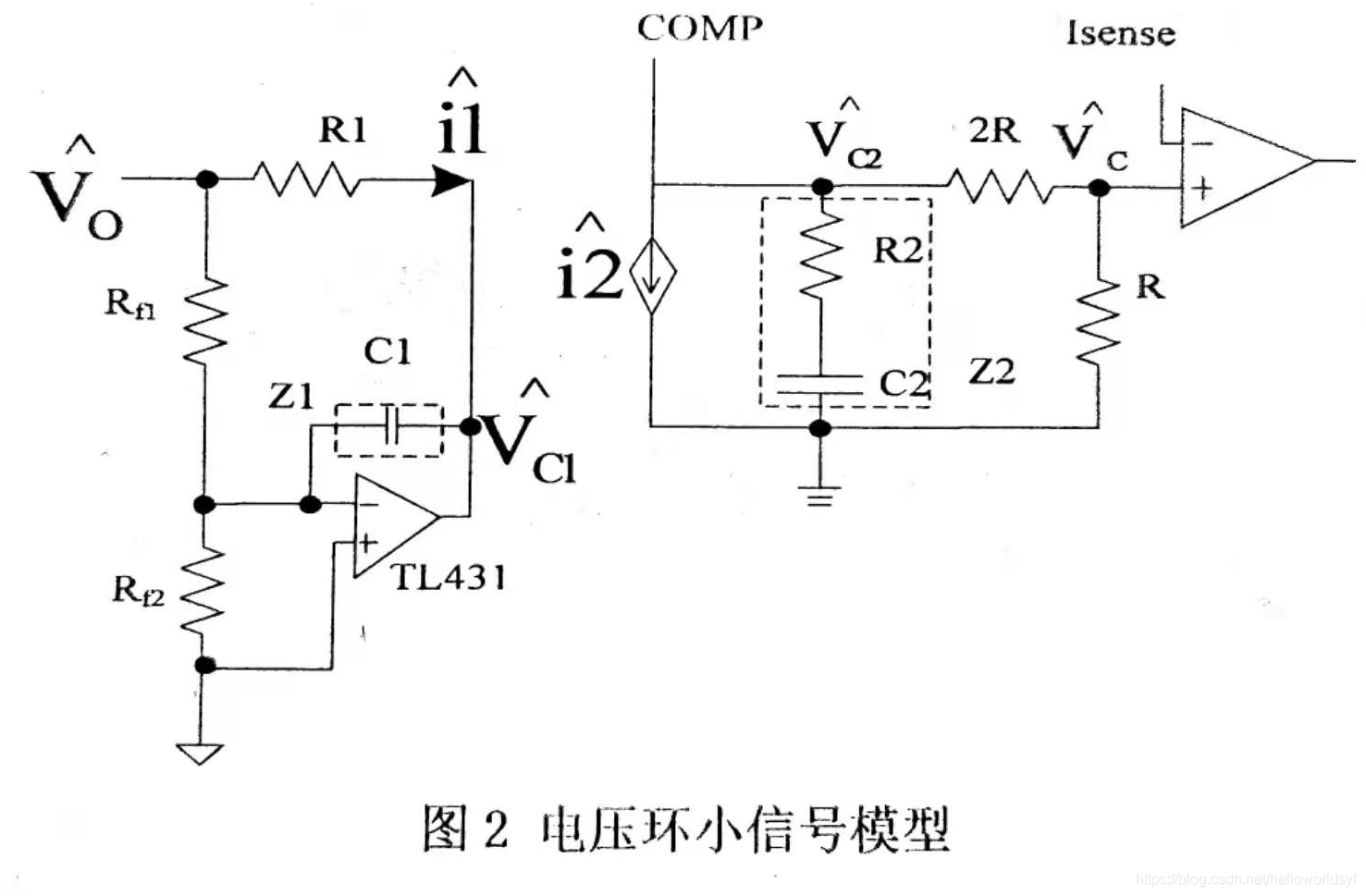
- 推导
因为运放虚地且输入接反相端 >>>
根据基尔霍夫电压定律 >>>
光耦相当于受控电流源 >>>
根据VCR公式 >>>
根据分压公式
最后得到 其中
;
最最后得到
- 特点
传递函数中包括一个比例环节(频带增益);积分环节
,惯性环节
,两个一阶微分环节

将带电流环功率级传递函数和进行相加叠加,

Rf2可以忽略的原因是它只起到了直流偏置的作用,不会出现在交流分析当中 (虽然不出现在传递函数中但会影响环路)
电流环
相当于前馈的作用,前馈回避了主要的延迟,校正几乎是瞬间的

电流采样:通过电阻采样和互感器采样,电阻采样的精度较高,可靠性好,但是损耗较大;互感器采样损耗偏小,但是可能会出现失真精度相对较低
带电流环的buck-boost


Ri为电流检测电阻,功率级传递函数的直流增益 ,副边电感
峰值电流控制
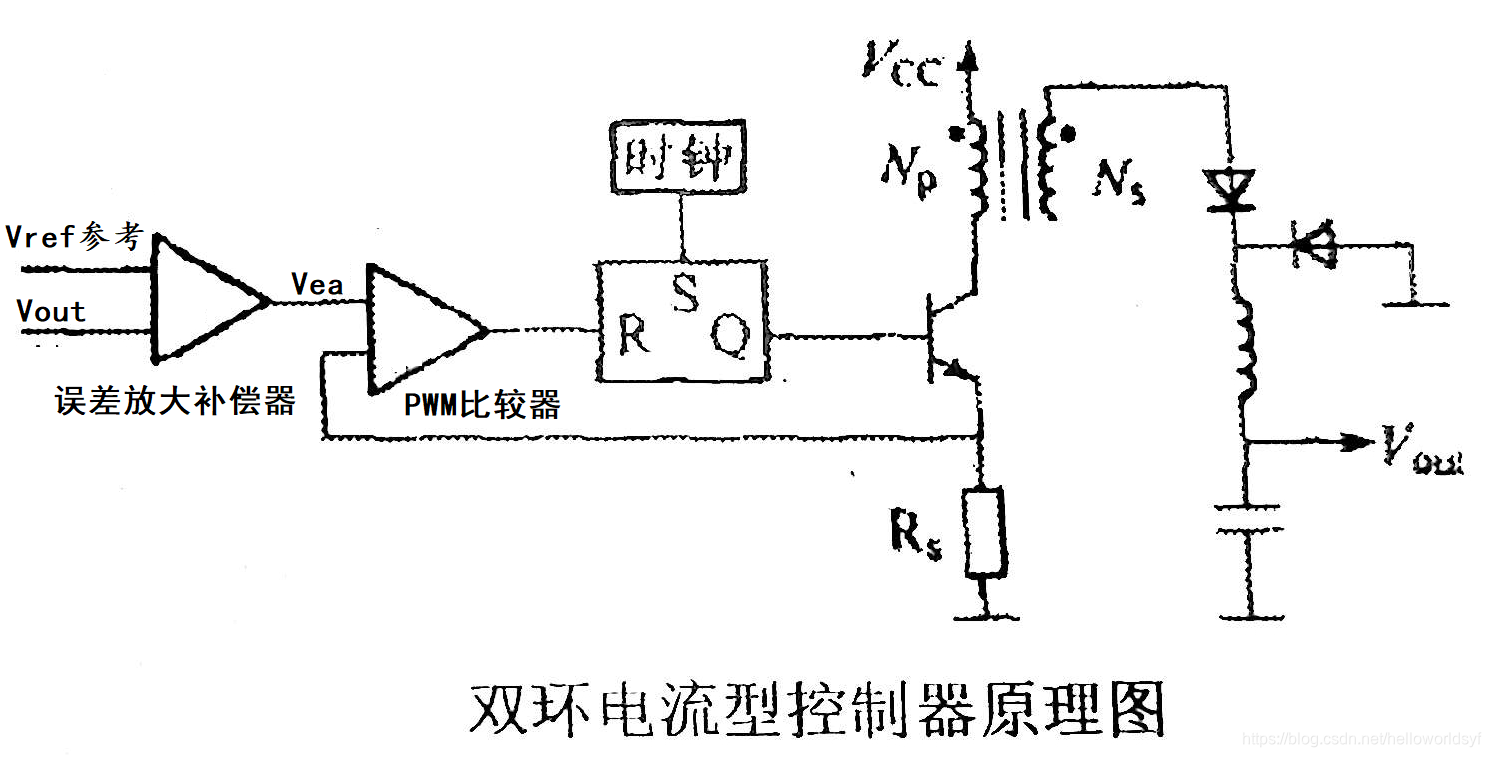
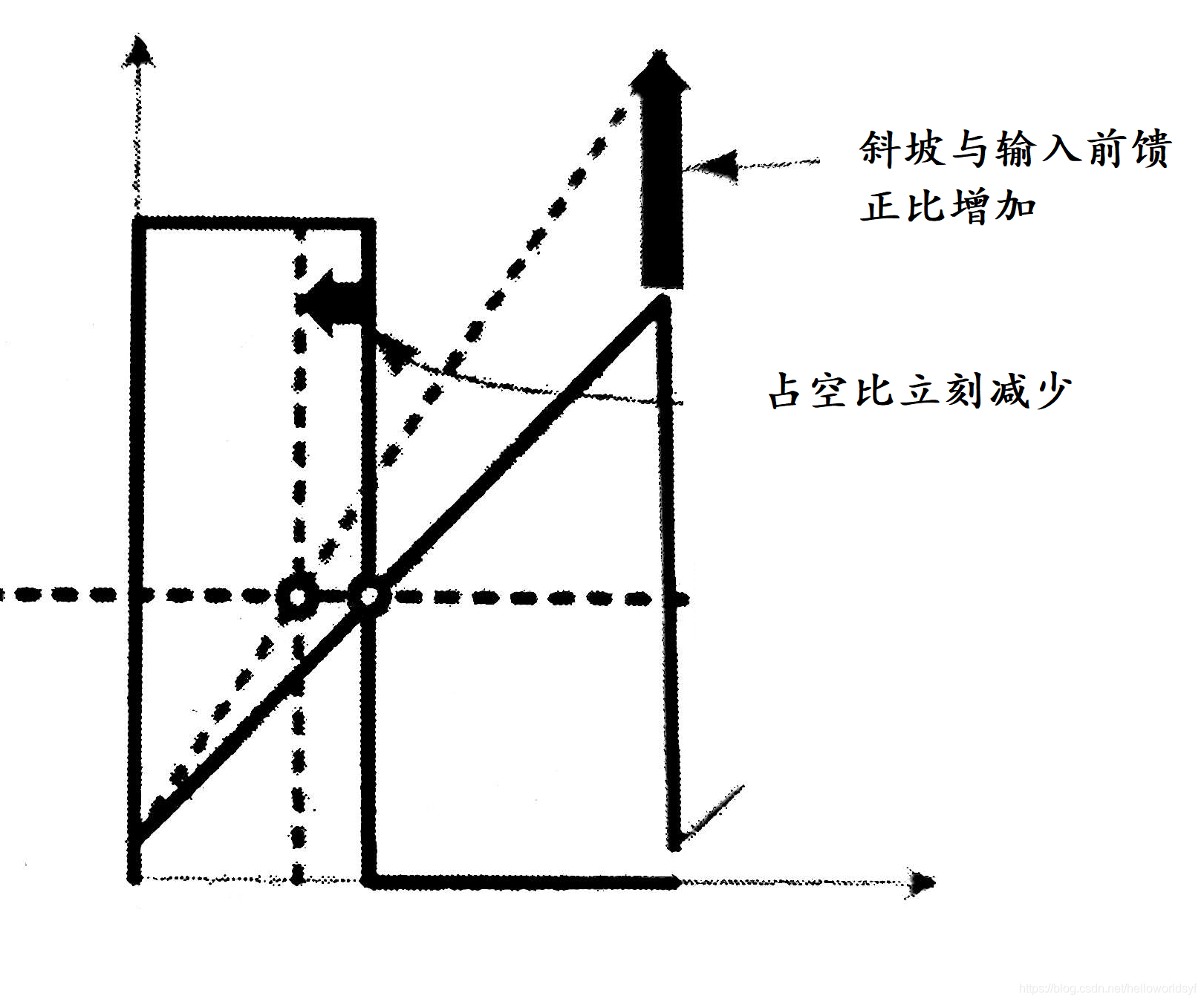
- 斜坡补偿
电流环中电流与误差补偿电压比较,从而得出占空比,以下分别是负载引起的扰动和输入电压引起的扰动
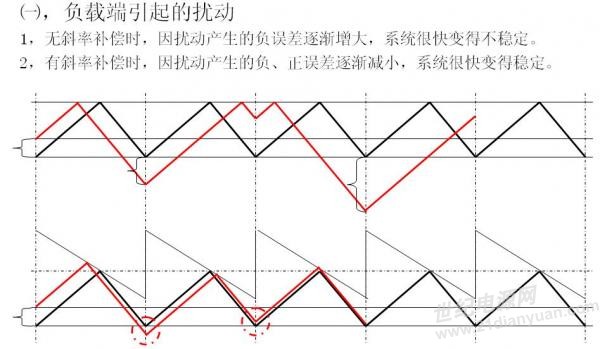
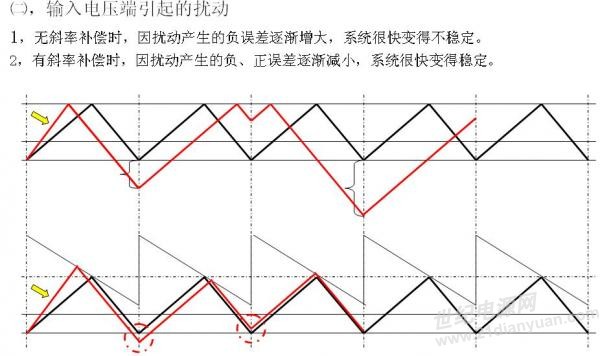


当占空比大于50%,会出现次谐波振荡,过一个周期会将扰动信号扩大,从而使系统发散
输入电压越大补偿越多,低压是可以
电路


设计
1.计算电感电流的下降沿
2.计算反应到初级的电感电流下降沿
3.计算初级测得的下降沿坡度
4.计算晶振充电时的坡度
5.采用叠加原理余斜坡补偿后电流输入端电压
6.计算斜坡补偿值
平均电流控制
环路设计策略
设计流程
-
计算功率级传递函数的直流增益
-
计算右半平面零点频率
-
计算功率级极点频率
-
确定补偿器频带增益
-
确定补偿器零点频率
零点频率选取为穿越频率的1/10
-
确定补偿器极点频率
极点频率可选取为右半平面零点重合的值,如ESR零点频率
零极点出现的位置
- 输出LC滤波器会引入 二重极点(会出现谐振频率那样的峰值)
- 电流环当占空比大于50%会引入 右半平面的极点 也就是发散
- CCM模式的升降压和升压拓扑会引入 右半平面的零点
升降压和降压功率级传递函数的区别
- 输出电容的等效串联电阻会引入 左半平面零点
虽然在左半平面,但会影响相角和可能会导致不再穿越0db轴,
1. 不能用于抵消LC滤波器会引入二重极点其一(因为不在理想位置)
2. 一半等效电阻很小,零点频率很高,在很远的位置,所有此时可以忽略
策略
- 保证穿越频率的开环增益斜率是-20db/dec
- 输出LC滤波器会引入二重极点,出现-40db/dec斜率,需要在交接频率附近引入两个一阶零点
- 保证穿越频率要小于1/6的开关频率(由于香浓采样定理小于1/2 而且要在穿越频率之前避免所有棘手的零极点)
过高则不稳定,过低则响应速度过慢
- 必须有两个零点抵消输出LC滤波器会引入二重极点
一个极点抵消等效电阻的零点
一个高频极点,一般是开关频率的一半,用于减少高频噪声的敏感度(环路的增益裕度是负数
在ccm模式下负载电流变化,伯德图不会变化、
杂项
垂直位移 直流增益
电感电流的上升斜坡斜率 (Vin-Vout)/L
当这个斜率很小的时候(Vin和小)会收到前沿的干扰








 本文详细探讨了电力电子控制系统的环路设计,包括开环与闭环系统、输出滤波器、功率级、PWM比较器、误差放大补偿器和反馈补偿等关键环节。介绍了零极点配置对系统稳定性的影响,强调了左半平面零极点的重要性以及右半平面零极点可能导致的不稳定性。此外,还详细阐述了电压环和电流环的控制策略,如123型补偿器电压环和峰值电流控制,并提供了设计流程和策略,以确保穿越频率的增益斜率和相位滞后满足稳定条件。
本文详细探讨了电力电子控制系统的环路设计,包括开环与闭环系统、输出滤波器、功率级、PWM比较器、误差放大补偿器和反馈补偿等关键环节。介绍了零极点配置对系统稳定性的影响,强调了左半平面零极点的重要性以及右半平面零极点可能导致的不稳定性。此外,还详细阐述了电压环和电流环的控制策略,如123型补偿器电压环和峰值电流控制,并提供了设计流程和策略,以确保穿越频率的增益斜率和相位滞后满足稳定条件。
















 2556
2556

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








