1.Bounding Boxes
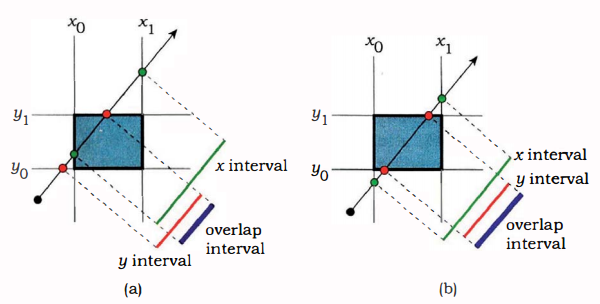
如下,没有和box 相交的线在 的 interval 和的interval 没有交集。相反,有相交的线的 两个interval 之间是交集的
bool
Box::hit(const Ray& ray, double& tmin, ShadeRec& sr) const {
double ox = ray.o.x; double oy = ray.o.y; double oz = ray.o.z;
double dx = ray.d.x; double dy = ray.d.y; double dz = ray.d.z;
double tx_min, ty_min, tz_min;
double tx_max, ty_max, tz_max;
double a = 1.0 / dx;
if (a >= 0) {
tx_min = (x0 - ox) * a;
tx_max = (x1 - ox) * a;
}
else {
tx_min = (x1 - ox) * a;
tx_max = (x0 - ox) * a;
}
double b = 1.0 / dy;
if (b >= 0) {
ty_min = (y0 - oy) * b;
ty_max = (y1 - oy) * b;
}
else {
ty_min = (y1 - oy) * b;
ty_max = (y0 - oy) * b;
}
double c = 1.0 / dz;
if (c >= 0) {
tz_min = (z0 - oz) * c;
tz_max = (z1 - oz) * c;
}
else {
tz_min = (z1 - oz) * c;
tz_max = (z0 - oz) * c;
}
double t0, t1;
int face_in, face_out;
// find largest entering t value
if (tx_min > ty_min) {
t0 = tx_min;
face_in = (a >= 0.0) ? 0 : 3;
}
else {
t0 = ty_min;
face_in = (b >= 0.0) ? 1 : 4;
}
if (tz_min > t0) {
t0 = tz_min;
face_in = (c >= 0.0) ? 2 : 5;
}
// find smallest exiting t value
if (tx_max < ty_max) {
t1 = tx_max;
face_out = (a >= 0.0) ? 3 : 0;
}
else {
t1 = ty_max;
face_out = (b >= 0.0) ? 4 : 1;
}
if (tz_max < t1) {
t1 = tz_max;
face_out = (c >= 0.0) ? 5 : 2;
}
if (t0 < t1 && t1 > kEpsilon) { // condition for a hit
if (t0 > kEpsilon) {
tmin = t0; // ray hits outside surface
sr.normal = get_normal(face_in);
}
else {
tmin = t1; // ray hits inside surface
sr.normal = get_normal(face_out);
}
sr.local_hit_point = ray.o + tmin * ray.d;
return (true);
}
else
return (false);
}
2. Triangles
三角形的定义
三角形的光线碰撞检测,分为两步:①光线是否hit 三角形所在的平面 ② hit point 是否在三角形以内。三角形所在平面任意一点p 可以表示为
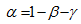
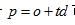
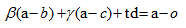
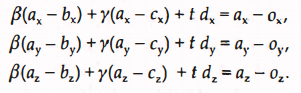
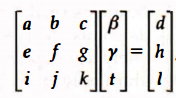
bool
Triangle::hit(const Ray& ray, double& tmin, ShadeRec& sr) const {
double a = v0.x - v1.x, b = v0.x - v2.x, c = ray.d.x, d = v0.x - ray.o.x;
double e = v0.y - v1.y, f = v0.y - v2.y, g = ray.d.y, h = v0.y - ray.o.y;
double i = v0.z - v1.z, j = v0.z - v2.z, k = ray.d.z, l = v0.z - ray.o.z;
double m = f * k - g * j, n = h * k - g * l, p = f * l - h * j;
double q = g * i - e * k, s = e * j - f * i;
double inv_denom = 1.0 / (a * m + b * q + c * s);
double e1 = d * m - b * n - c * p;
double beta = e1 * inv_denom;
if (beta < 0.0)
return (false);
double r = r = e * l - h * i;
double e2 = a * n + d * q + c * r;
double gamma = e2 * inv_denom;
if (gamma < 0.0 )
return (false);
if (beta + gamma > 1.0)
return (false);
double e3 = a * p - b * r + d * s;
double t = e3 * inv_denom;
if (t < kEpsilon)
return (false);
tmin = t;
sr.normal = normal;
sr.local_hit_point = ray.o + t * ray.d;
return (true);
} 3.Other Objects
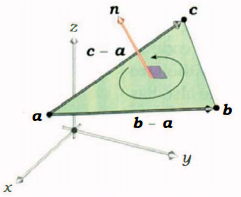
圆形由中心c,半径r,法线n确定 ,同理首先是判断是不是在圆形所在的平面,然后判断和圆心的距离,既可以看出是否和圆形有相交。 因为开方运算耗时,所以直接判断平方的大小








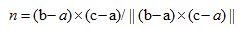
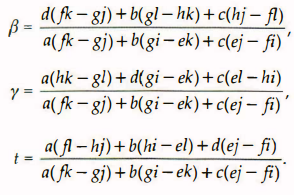















 8693
8693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










