工具vivado2018.3,modelsim10.6d
在数字电路中如何来实现二进制的加法运算呢?
例如计算两个十进制数的加法。
76+57=133
76的二进制数01001100
57的二进制数00111001
加法进位 11110000
加法结果 10000101
以上就是二进制加法运算过程,满二进一,加法运算第一个进位位设为0。
半加器half add
是一个不带进位的二进制加法器
| 输入 | 输出 | ||
| A输入 | B输入 | C进位 | S结果 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
从上面的真值表可以很简单的看出来
assign s = a ^ b;
assign c = a & b;使用vivado设计一个半加器的结构如下图所示。

那么全加器和半加器的区别在哪儿呢?
全加器
全加器在半加器的基础上引入了进位。
全加器真值表
| 输入 | 输出 | |||
| A输入 | B输入 | Cin | C进位 | S结果 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
运算逻辑式
assign S = a^b^cin;
assign cout = ((a&b) | (cin&(a^b)));全加器的直接实现

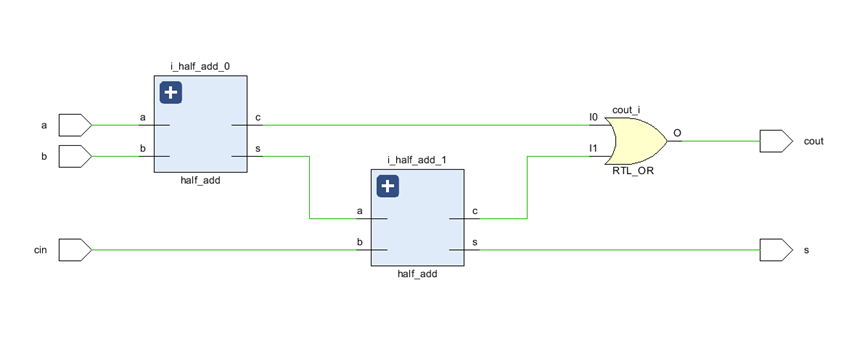
也可以使用两个半加器实现全加器,a与b的接入半加器0的输入,输出中间进位c和中间结果s。在将进位输入cin和中间进位c输入到半加器1,输出中间进位c和结果s。进位输出cout等于两个中间进位c的或。
// *********************************************************************************/
// Project Name :
// Author : i_huyi
// Email : i_huyi@qq.com
// Creat Time : 2024/10/21 9:25:25
// File Name : .v
// Module Name :
// Called By :
// Abstract :两个半加器组成的全加器
//
// CopyRight(c) 2020, xxx xxx xxx Co., Ltd..
// All Rights Reserved
//
// *********************************************************************************/
// Modification History:
// 1. initial
// *********************************************************************************/
// *************************
// MODULE DEFINITION
// *************************
`timescale 1 ns / 1 ps
module full_add#(
parameter U_DLY = 1
)
(
input wire a , // 加数输入
input wire b , // 加数输入
input wire cin , // 进位输入
output wire s , // 结果输出
output wire cout // 进位输出
);
//----------------------------------------------
// localparam
//----------------------------------------------
//----------------------------------------------
// register
//----------------------------------------------
//----------------------------------------------
// wire
//----------------------------------------------
wire c1 ;
wire c2 ;
wire sum ;
//----------------------------------------------
// assign
//----------------------------------------------
assign cout = c1 | c2;
//------------------------------------------------------------
//------------------------------------------------------------
half_add i_half_add_0(
.a (a ), // (input ) (input )
.b (b ), // (input ) (input )
.c (c1 ), // (output) (output)
.s (sum )// (output) (output)
);
half_add i_half_add_1(
.a (sum ), // (input ) (input )
.b (cin ), // (input ) (input )
.c (c2 ), // (output) (output)
.s (s )// (output) (output)
);
//------------------------------------------------------------
//------------------------------------------------------------
//------------------------------------------------------------
//------------------------------------------------------------
endmodule
上面介绍了单bit的加法器的实现,那么如果是多bit的加法器怎么实现呢?
波纹进位加法器
如果我们实现一个4位数的加法器,而全加器是单bit的加法器,我们可以将全加器级联起来就得到了一个波纹进位加法器。
// *********************************************************************************/
// Project Name :
// Author : i_huyi
// Email : i_huyi@qq.com
// Creat Time : 2024/10/21 9:32:11
// File Name : .v
// Module Name :
// Called By :
// Abstract :多bit加法器
//
// CopyRight(c) 2020, xxx xxx xxx Co., Ltd..
// All Rights Reserved
//
// *********************************************************************************/
// Modification History:
// 1. initial
// *********************************************************************************/
// *************************
// MODULE DEFINITION
// *************************
`timescale 1 ns / 1 ps
module full_add_4bit#(
parameter U_DLY = 1
)
(
input wire [3:0] a , // 加数输入
input wire [3:0] b , // 被加数输入
output wire [3:0] s , // 结果输出
output wire c // 进位输出
);
//----------------------------------------------
// localparam
//----------------------------------------------
//----------------------------------------------
// register
//----------------------------------------------
//----------------------------------------------
// wire
//----------------------------------------------
wire [4:0] carry ;
//----------------------------------------------
// assign
//----------------------------------------------
assign carry[0] = 1'b0;
assign c = carry[4];
//------------------------------------------------------------
//------------------------------------------------------------
full_add u_full_add_0(
.a (a[0] ), // (input ) 加数输入
.b (b[0] ), // (input ) 加数输入
.cin (carry[0] ), // (input ) 进位输入
.s (s[0] ), // (output) 结果输出
.cout (carry[1] )// (output) 进位输出
);
full_add u_full_add_1(
.a (a[1] ), // (input ) 加数输入
.b (b[1] ), // (input ) 加数输入
.cin (carry[1] ), // (input ) 进位输入
.s (s[1] ), // (output) 结果输出
.cout (carry[2] )// (output) 进位输出
);
full_add u_full_add_2(
.a (a[2] ), // (input ) 加数输入
.b (b[2] ), // (input ) 加数输入
.cin (carry[2] ), // (input ) 进位输入
.s (s[2] ), // (output) 结果输出
.cout (carry[3] )// (output) 进位输出
);
full_add u_full_add_3(
.a (a[3] ), // (input ) 加数输入
.b (b[3] ), // (input ) 加数输入
.cin (carry[3] ), // (input ) 进位输入
.s (s[3] ), // (output) 结果输出
.cout (carry[4] )// (output) 进位输出
);
//------------------------------------------------------------
//------------------------------------------------------------
//------------------------------------------------------------
//------------------------------------------------------------
endmodule

输入数据的bit0和cin进入全加器0,等待计算出结果后cout输入到全加器1的cin位,等待计算出结果后输入到全加器2的cin位,最后计算出的结果输入到全加器3的cin。最后计算出结果。
超前进位加法器
全加器的门延迟

上图是一个全加器的逻辑组成,可以看到全加器的最长路径是经过((a^b)&cin) | (a&b)经过一个异或门,在经过一个与门在经过一个异或门三级门延迟到达cout。
而前面使用波纹进位加法器需要将全加器级联。
设计一个四位波纹进位加法器所经过的延迟。

需要经过四级全加器,经过第一级延迟为3个门延迟,第二级cout的延迟为2。所以4级全加器级联的波纹进位加法器延迟为3+2*3=9级门延迟。
实际上可以使用资源换速度的方法,使用超前进位加法器来减少门延迟。
波纹进位加法器的延迟之所以大,就是每一次计算需要等待上一次计算结果的进位来进行计算。如果将这个等待进位时间消除,就可以减少门延迟。
根据全加器的真值表,还可以得出
cout=AB+Acin+bcin
cout=AB+(A+B)cin
这里将AB称为generates生成信号G
将A+B称为propagates传输信号P
cout=G+Pcin
那么一个4位加法器
C1=G0+P0C0
C2=G1+P1C1
C3=G2+P2C2
C4=G3+P3C3
将上述式子改写为
C1=G0+P0C0
C2=G1+P1(G0+P0C0)=G1+P1G0+P1P0C0
C3=G2+P2(G1+P1G0+P1P0C0)=G2+P2G1+P2P1G0+P2P1P0C0
C4=G3+P3(G2+P2G1+P2P1G0+P2P1P0C0)=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0C0
可以最长的路径P3P2P1P0C0写为(A3+B3)&(A2+B2)&(A1+B1)&(A0+B0)&C0数据每一位相或后再相与再经过一个或门后输出C4,再经过Si=Ai^Bi^Ci异或门后输出。共计四级延迟。
// *********************************************************************************/
// Project Name :
// Author : i_huyi
// Email : i_huyi@qq.com
// Creat Time : 2024/10/21 9:50:52
// File Name : .v
// Module Name :
// Called By :
// Abstract :超前进位链的加法器for 4 bit
// s = A^B^Cin;
// cout = AB+(A+B)Cin;
// AB:generates生成信号G
// A+B:propagates传输信号P
// cout = G + PCin;
// for 4bit
// C1 = G0 + P1C0;
// C2 = C1 + P1C1;
// C3 = C2 + P2C2;
// C4 = C3 + P3C3;
// 超前进位无需等待CN,直接计算CN
// C1 = G0 + P0C0;
// C2 = G1 + P1(G0+P1C0)=G1 + P1G0 + P1P0C0;
// C3 = G2 + P2G1 + P2P1G0 + P2P1P0C0;
// C4 = G3 + P3P2G1 + P3P2P1G0 + P3P2P1P0C0;
//
// CopyRight(c) 2020, xxx xxx xxx Co., Ltd..
// All Rights Reserved
//
// *********************************************************************************/
// Modification History:
// 1. initial
// *********************************************************************************/
// *************************
// MODULE DEFINITION
// *************************
`timescale 1 ns / 1 ps
module carry_look_add#(
parameter WIDTH = 4 ,
parameter U_DLY = 1
)
(
input [WIDTH-1:0] in1 , //
input [WIDTH-1:0] in2 , //
input cin , // (input )
output [WIDTH-1:0] S , //
output Cout //
);
//----------------------------------------------
// localparam
//----------------------------------------------
//----------------------------------------------
// register
//----------------------------------------------
//----------------------------------------------
// wire
//----------------------------------------------
wire [WIDTH-1:0] G ; //generates;
wire [WIDTH-1:0] P ; //propagates;
wire [WIDTH:0] C ;
//----------------------------------------------
// assign
//----------------------------------------------
//G
generate
genvar i;
for(i = 0 ; i < WIDTH ; i = i + 1)begin:gp
assign G[i] = in1[i] & in2[i];
assign P[i] = in1[i] | in2[i];
assign S[i] = in1[i] ^ in2[i] ^ C[i];
end
endgenerate
//C
assign C[0] = cin;
assign C[1] = G[0] | (P[0] & C[0]);
assign C[2] = G[1] | (P[1] & G[0]) | (P[1] & P[0] & C[0]);
assign C[3] = G[2] | (P[2] & G[1]) | (P[2] & P[1] & G[0]) | (P[2] & P[1] & P[0] & C[0]);
assign C[4] = G[3] | (P[3] & G[2]) | (P[3] & P[2] & G[1]) | (P[3] & P[2] & P[1] & G[0]) | (P[3] & P[2] & P[1] & P[0] & C[0]);
//Cout
assign Cout = C[4];
//------------------------------------------------------------
//------------------------------------------------------------
//------------------------------------------------------------
//------------------------------------------------------------
//------------------------------------------------------------
//------------------------------------------------------------
endmodule

























 245
245

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








