无人机六旋翼数学建模[matlab-simulink]

写在前面，这篇文章是借鉴Drexel University 的Senior Design project的matlab simulink四旋翼模型，在此基础上针对六旋翼进行的基本改进，这里只对“+”型模型进行了改造，学习追溯帖。

数学模型

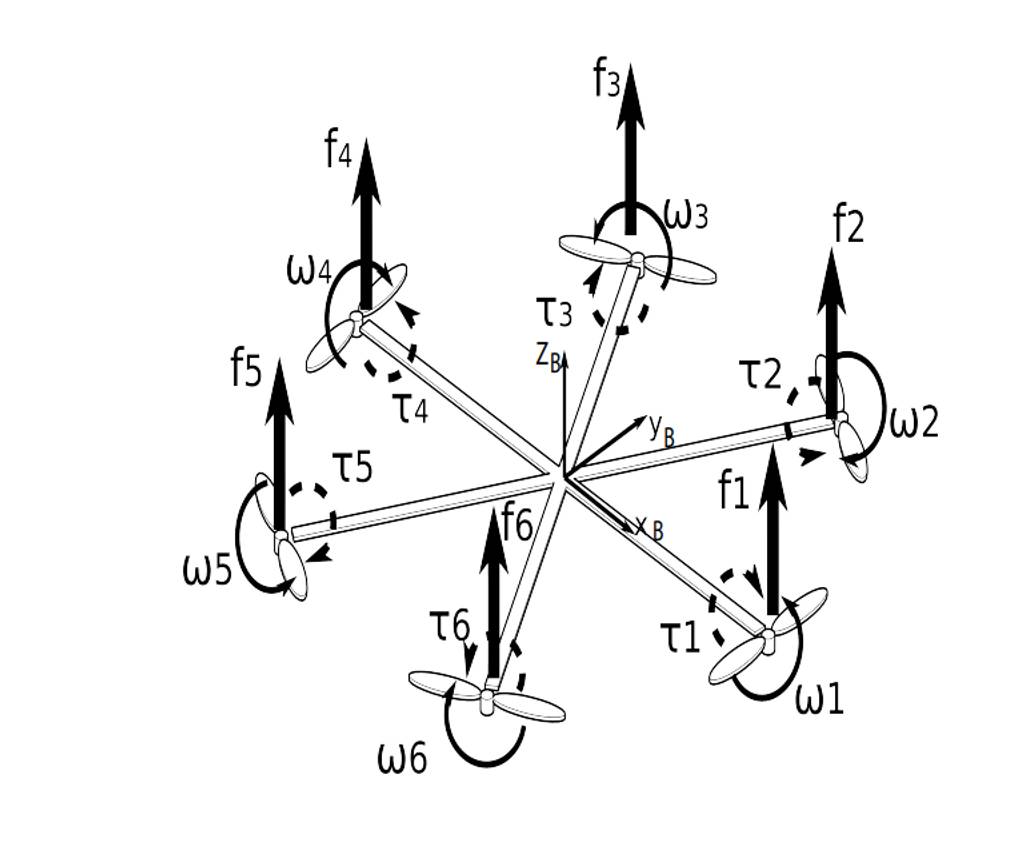
自然坐标系下，以无人机本身为参考系

$${}^b{\dot{\mathrm{V}}}_{CM\mid i}^b$$
说明：

1. 基础变量是线性加速度
2. 左上：以体坐标系下的微分
3. 右上：体坐标系下的加速度
4. 下标：这个变量是质心相对于惯性系
5. 这里使用+号坐标系法，x的正方向指向motor1

Mass Moment of Inertia Matrix 质量惯性矩阵

对应轴的转动惯量
$$J^b=\left[\begin{array}{ccc}{J}_{xx}& 0& 0\\ 0& J_{yy}& 0\\ 0& 0& J_{zz}\end{array}\right]$$

推力系数Thrust Coefficient

$$T=C_T\rho A_r{r}^2{\varpi }^2$$
其中：
ρ是空气密度
CT是特定一个旋翼的系数
Ar是螺旋桨旋转的扫掠面积
r是旋翼半径

$$\varpi$$
是旋翼角速度

Torque Coefficient 转矩系数

马达效应

A current-carrying wire or coil can exert a force on a permanent magnet. This is called the motor effect
同时考虑马达效应和推力，和旋翼的角速度成正比
将常量化为一个系数最后得到：

$$\begin{gathered} Q=c_Q{\varpi }^2 \\ T=c_T{\varpi }^2 \end{gathered}$$

初试矩阵的建设 initial matrix construction

通过输入测试得到的数据，我们提供了一个程序来方便计算这些系统系数，通过这些信息，我们能够建立一个Initial matrix，分别表示推力以及体坐标系下各轴转矩。

$$\left[\begin{array}{l}\Sigma T\\ {\tau }_{\varphi }\\ {\tau }_{\theta }\\ {\tau }_{\psi }\end{array}\right]=\left[\begin{array}{cccccc}{c}_T& c_T& c_T& c_T& c_T& c_T\\ 0& \frac{\sqrt{3}}{2}{d}_{+}{c}_T& \frac{\sqrt{3}}{2}{d}_{+}{c}_T& 0& -\frac{\sqrt{3}}{2}{d}_{+}{c}_T& -\frac{\sqrt{3}}{2}{d}_{+}{c}_T\\ -d_{+}{c}_T& -\frac{1}{2}{d}_{+}{c}_T& \frac{1}{2}{d}_{+}{c}_T& d_{+}{c}_T& \frac{1}{2}{d}_{+}{c}_T& -\frac{1}{2}{d}_{+}{c}_T\\ c_Q& -c_Q& c_Q& -c_Q& c_Q& -c_Q\end{array}\right]\left[\begin{array}{l}{\varpi }_1^2\\ {\varpi }_2^2\\ {\varpi }_3^2\\ {\varpi }_4^2\\ {\varpi }_5^2\\ {\varpi }_6^2\end{array}\right]$$

百分比控制 Throttle Command Relation

调速命令

  为了控制，由于系数是从推力转矩与rpm之间转换的，所以需要线性回归来将调速命令转换成为rpm

$${\varpi }_{SS}=(\text{ Throttle }\%)c_R+b$$
解释：

$$\varpi 是期望稳定的转速。$$
throttle是比例
Cr是rpm的转换系数，b是y的偏移

陀螺力Gyroscopic Forces

陀螺力是由每个马达的转动惯量，以及转速，还有角速度Roll and Pitch rate，反力的方向参考这篇文章，简单来说，反力的方向是：
$$\tau =T=I{\omega }_{马达}\times {\omega }_{R、P、Q的方向}$$

$$\begin{array}{c}{\tau }_{{\varphi }_{\text{gyro }}}=J_{m}Q\left(\frac{\pi }{30}\right)\left({\varpi }_1-{\varpi }_2+{\varpi }_3-{\varpi }_4+{\varpi }_5-{\varpi }_6\right)\\ {\tau }_{{\theta }_{\text{gyro }}}=J_{m}P\left(\frac{\pi }{30}\right)\left(-{\varpi }_1+{\varpi }_2-{\varpi }_3+{\varpi }_4-{\varpi }_5+{\varpi }_6\right)\end{array}$$
pi/30代表从rpm转换到角度速度的转换

最后方程建设

将之前得到的转矩和陀螺力加起来

$$M_{A,T}^b=\left[\begin{array}{c}\frac{\sqrt{3}}{2}{d}_{+}{c}_T{\varpi }_2^2+\frac{\sqrt{3}}{2}{d}_{+}{c}_T{\varpi }_3^2-\frac{\sqrt{3}}{2}{d}_{+}{c}_T{\varpi }_5^2-\frac{\sqrt{3}}{2}{d}_{+}{c}_T{\varpi }_6^2+J_{m}Q\left(\frac{\pi }{30}\right)\left({\varpi }_1-{\varpi }_2+{\varpi }_3-{\varpi }_4+{\varpi }_5-{\varpi }_6\right)\\ -d_{+}{c}_T{\varpi }_1^2+-\frac{1}{2}{d}_{+}{c}_T{\varpi }_2^2+\frac{1}{2}{d}_{+}{c}_T{\varpi }_3^2+d_{+}{c}_T{\varpi }_4^2+\frac{1}{2}{d}_{+}{c}_T{\varpi }_5^2-\frac{1}{2}{d}_{+}{c}_T{\varpi }_6^2+J_{m}P\left(\frac{\pi }{30}\right)\left(-{\varpi }_1+{\varpi }_2-{\varpi }_3+{\varpi }_4-{\varpi }_5+{\varpi }_6\right)\\ c_Q{\varpi }_1^2-c_Q{\varpi }_2^2+c_Q{\varpi }_3^2-c_Q{\varpi }_4^2+c_Q{\varpi }_5^2-c_Q{\varpi }_6^2\end{array}\right]$$

  这里

$$M_{A,T}^b$$
代表由推力空气动力学推力和扭矩生成的力矩，主体部分收到的推力可以由以下表达。

$${\mathrm{F}}_{A,T}^b=\left[\begin{array}{c}0\\ 0\\ c_T\left({\varpi }_1^2+{\varpi }_2^2+{\varpi }_3^2+{\varpi }_4^2+{\varpi }_5^2+{\varpi }_6^2\right)\end{array}\right]$$
其中f代表在基坐标系下，由空气阻力和推力同时作用下的力。

状态方程

角速度状态方程，其中包含每个角度的状态方程：

$${}^b{\dot{\omega }}_{b\mid i}^b={\left(J^b\right)}^{-1}\left[M_{A,T}^b-{\Omega }_{b\mid i}^b{J}^b{\omega }_{b\mid i}^b\right]=\left[\begin{array}{c}\dot{P}\\ \dot{Q}\\ \dot{R}\end{array}\right]$$
其中：后面一项可以理解为刚体的科氏加速度，推导借鉴这里以下是借鉴推导部分，Ω矩阵将wb叉乘转化为点乘
$${\Omega }_{b\mid i}^b=\left[\begin{array}{ccc}0& -\mathrm{R}& \mathrm{Q}\\ \mathrm{R}& 0& -\mathrm{P}\\ -\mathrm{Q}& \mathrm{P}& 0\end{array}\right]$$
这个部分是角速度

$${\omega }_{b\mid i}^b=\left[\begin{array}{l}P\\ Q\\ R\end{array}\right]$$

下一个状态方程是欧拉运动方程，描述了欧拉角在惯性系下的运动速率

$$\dot{\Phi }=H(\Phi ){\omega }_{b\mid i}^b=\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]$$

笛卡尔坐标系下，使用旋转矩阵转换描述机体坐标系表达的一切向量。

利用欧拉角组成旋转矩阵

$${\mathrm{u}}^b=\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{c}(\varphi )& \mathrm{s}(\varphi )\\ 0& -\mathrm{s}(\varphi )& \mathrm{c}(\varphi )\end{array}\right]\left[\begin{array}{ccc}\mathrm{c}(\theta )& 0& -\mathrm{s}(\theta )\\ 0& 1& 0\\ \mathrm{s}(\theta )& 0& \mathrm{c}(\theta )\end{array}\right]\left[\begin{array}{ccc}\mathrm{c}(\psi )& \mathrm{s}(\psi )& 0\\ -\mathrm{s}(\psi )& \mathrm{c}(\psi )& 0\\ 0& 0& 1\end{array}\right]{\mathrm{u}}^i$$
cb是旋转方程相乘得到
$$C_{b\mid i}=\left[\begin{array}{ccc}\mathrm{c}(\theta )\mathrm{c}(\psi )& \mathrm{c}(\theta )\mathrm{s}(\psi )& -\mathrm{s}(\theta )\\ (-\mathrm{c}(\varphi )\mathrm{s}(\psi )+\mathrm{s}(\varphi )\mathrm{s}(\theta )c(\psi ))& (c(\varphi )c(\psi )+s(\varphi )s(\theta )s(\psi ))& \mathrm{s}(\varphi )\mathrm{c}(\theta )\\ (s(\varphi )s(\psi )+c(\varphi )s(\theta )c(\psi ))& (-s(\varphi )c(\psi )+c(\varphi )s(\theta )s(\psi ))& \mathrm{c}(\varphi )\mathrm{c}(\theta )\end{array}\right]$$
这可以用来解决速度和位置方程
通过引入这个旋转矩阵
角速度可以表达为：

$${\omega }_{b\mid i}^b=\left[\begin{array}{c}\dot{\varphi }\\ 0\\ 0\end{array}\right]+C_{\varphi }\left(\left[\begin{array}{l}0\\ \dot{\theta }\\ 0\end{array}\right]+C_{\theta }\left[\begin{array}{l}0\\ 0\\ \dot{\psi }\end{array}\right]\right)$$

最后欧拉运动学方程能用如下的的运动学方程来表示

$$\dot{\Phi }=\left[\begin{array}{c}\dot{\varphi }\\ \dot{\theta }\\ \dot{\psi }\end{array}\right]=\left[\begin{array}{ccc}1& t(\theta )s(\varphi )& t(\theta )c(\varphi )\\ 0& c(\varphi )& -s(\varphi )\\ 0& s(\varphi )/c(\theta )& c(\varphi )/c(\theta )\end{array}\right]\left[\begin{array}{l}P\\ Q\\ R\end{array}\right]=H(\Phi ){\omega }_{b\mid i}^b$$
虽然这种方法很有效，但是有一个缺陷，当θ等于正负90度时，有奇异点出现，这样当飞行器的的pitch角度达到正负90时候，精确性就要打折了，
但是对于保守的设计来说够了。
解决方法：
使用四元数来模拟就可以解决

   下一个是速度状态方程

$${}^b{\dot{\mathrm{V}}}_{CM\mid i}^b=\left(\frac{1}{m}\right){\mathrm{F}}_{A,T}^b+g^b-{\Omega }_{b\mid i}^b{\omega }_{CM\mid i}^b=\left[\begin{array}{c}\dot{U}\\ \dot{V}\\ \dot{W}\end{array}\right]$$
考虑施加在主体质心的加速度和力
这里开头是线性加速度实在对应惯性系下的线性加速度，变量m是总质量，gb是转换以后的重力加速度，使用这个可以计算出xyz方向的加速度
  最后一个状态方程是位置状态方程，描述了无人机质心的线性速度

$$i{\dot{\mathrm{P}}}_{CM\mid i}^i=C_{i\mid b}{\mathrm{V}}_{CM\mid i}^b=\left[\begin{array}{c}\dot{X}\\ \dot{Y}\\ \dot{Z}\end{array}\right]$$
这里v代表无人机的速度由c来转化以后的速度，让我们得到无人机的速度。

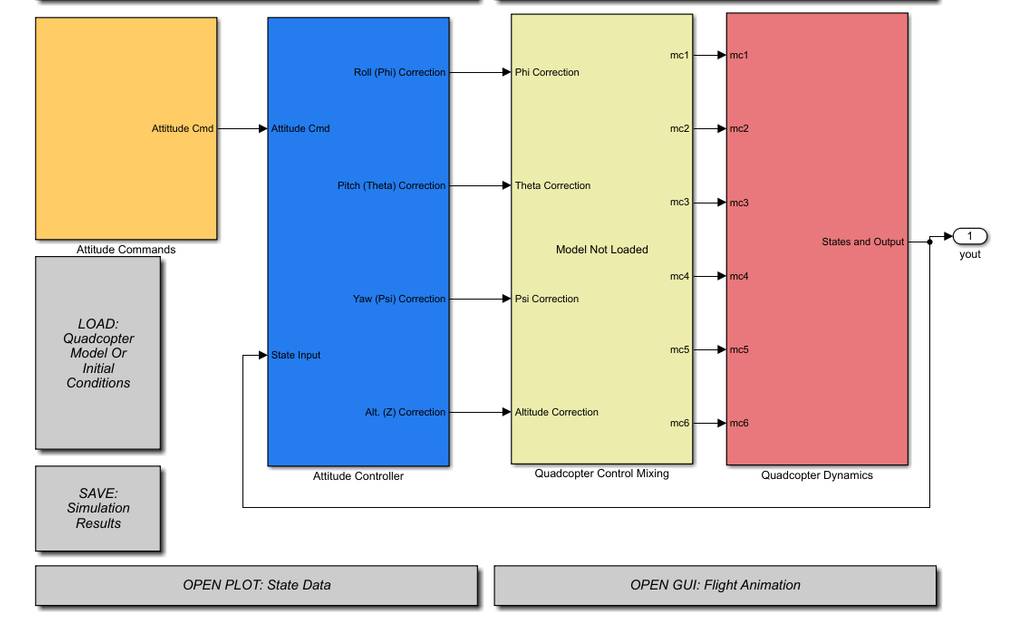
工程体现

在工程中我们需要修改电机的数量，初试条件的举矩阵等，本着不多事的原则，我只修改了电机数量，内外反馈没有进行改动。
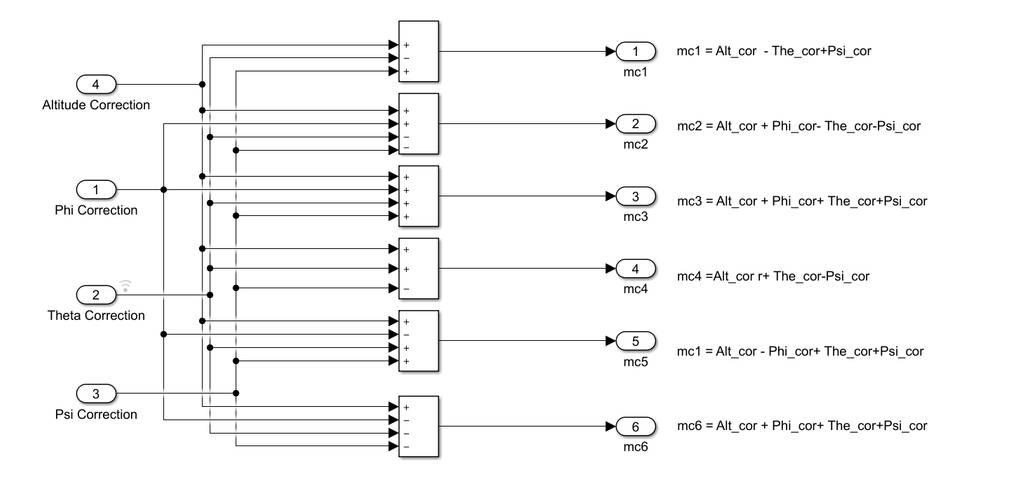
这是修改内容
整体改了六个旋翼，改了控制器和输入输出状态，反馈回路没有修改。

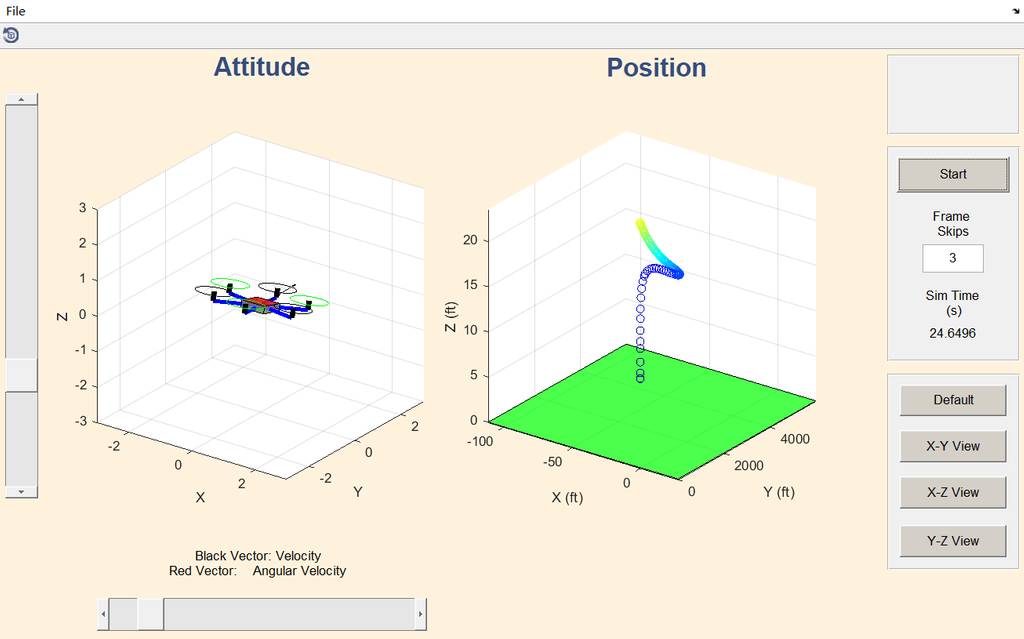
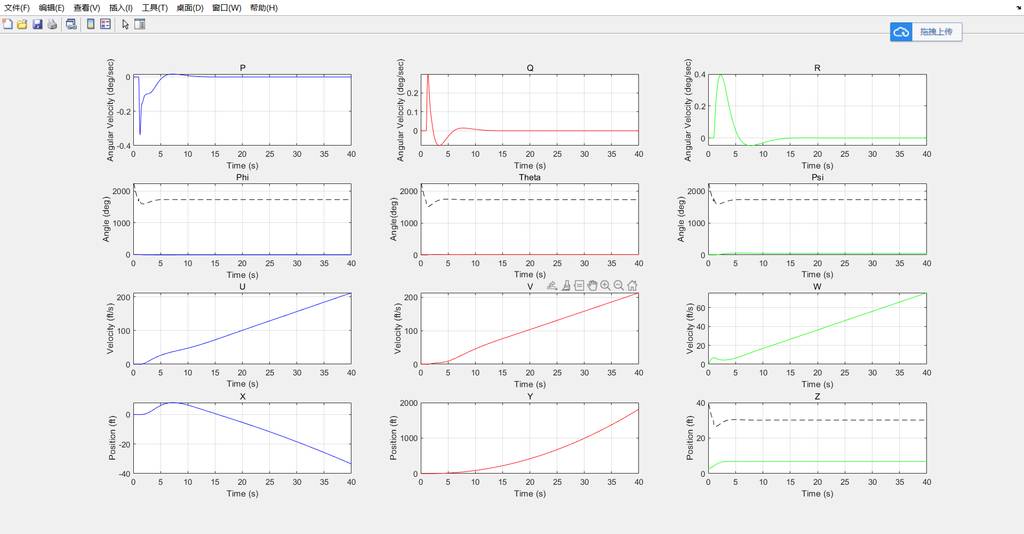
经过测试，整体上还是比较稳定的：

可视化界面，这里修改了模型。

状态指标：

文件链接：私聊联系我，不要直接拍。
【闲鱼】https://m.tb.cn/h.Utxt7WY?tk=8mCvdOGY6Ck CZ0001 「我在闲鱼发布了【六旋翼SIMULINK仿真模型PID】」
点击链接直接打开