CNN-LSTM与ConvLSTM的区别
摘要
在时间序列预测、视频分析和气象模拟等领域,如何同时建模空间特征和时间依赖是核心挑战。传统LSTM擅长时序建模,但难以捕捉空间特征;传统CNN擅长空间特征提取,却对时序动态不敏感。为了融合二者的优势,学界提出了两种典型方案:CNN-LSTM和ConvLSTM。这两种架构看似相似,实则代表了两种截然不同的时空建模哲学。本文将从原理、结构、性能和应用场景深入解析二者的区别。本文侧重在讲解区分,理解构建convLSTM的思想,具体构建的代码见参考文献。
一、架构设计的本质差异
1.1 CNN-LSTM:时空级联的“分治策略”
CNN-LSTM采用级联式设计,将空间特征提取与时间建模分为两个独立阶段:
-
空间特征压缩
通过CNN(如一维或二维卷积)提取输入数据的局部空间特征,例如图像中的纹理或时间序列中的局部波动;
-
时间序列建模
将CNN输出的特征图展平为向量,输入LSTM进行时序建模
这种结构本质上是一种特征工程流水线,先通过CNN降维(升维)再处理时序关系。例如在股票预测中,CNN可能提取价格波动中的短期趋势,LSTM则学习长期周期规律。
1.2 ConvLSTM:时空融合的“统一场论”
ConvLSTM则是细胞级的时空联合建模,将卷积运算嵌入LSTM的门控机制:
-
门控卷积化
输入门、遗忘门、输出门的矩阵乘法被替换为卷积操作,直接处理保留空间维度的张量
(如5D张量[batch, time, height, width, channels]);
-
时空状态传递
细胞状态(Cell State)和隐藏状态(Hidden State)均为3D特征图,保留了空间结构信息。
这种设计使其能直接建模时空耦合现象,例如云团移动时形状变化与运动轨迹的关联。
二、数学表达的范式冲突
2.1 CNN-LSTM的线性分解
CNN-LSTM的运算可分解为:
空间阶段:
F
t
=
CNN
(
X
t
)
F_t = \text{CNN}(X_t)
Ft=CNN(Xt)
时间阶段:
h
t
,
c
t
=
LSTM
(
Flatten
(
F
t
)
,
h
t
−
1
,
c
t
−
1
)
h_t, c_t = \text{LSTM}(\text{Flatten}(F_t), h_{t-1}, c_{t-1})\\
ht,ct=LSTM(Flatten(Ft),ht−1,ct−1)
其中空间特征
F
t
F_t
Ft被展平后失去空间维度,仅保留通道信息。
遗忘门(Forget Gate)
:
f
t
=
σ
(
W
f
⋅
[
h
t
−
1
,
x
t
]
+
b
f
)
输入门(Input Gate)
:
i
t
=
σ
(
W
i
⋅
[
h
t
−
1
,
x
t
]
+
b
i
)
候选细胞状态(Candidate)
:
C
~
t
=
tanh
(
W
C
⋅
[
h
t
−
1
,
x
t
]
+
b
C
)
细胞状态更新(Cell State)
:
C
t
=
f
t
⊙
C
t
−
1
+
i
t
⊙
C
~
t
输出门(Output Gate)
:
o
t
=
σ
(
W
o
⋅
[
h
t
−
1
,
x
t
]
+
b
o
)
隐藏状态(Hidden State)
:
h
t
=
o
t
⊙
tanh
(
C
t
)
\begin{aligned} \text{遗忘门(Forget Gate)} &: \quad f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) \\ \text{输入门(Input Gate)} &: \quad i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) \\ \text{候选细胞状态(Candidate)} &: \quad \tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) \\ \text{细胞状态更新(Cell State)} &: \quad C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t \\ \text{输出门(Output Gate)} &: \quad o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \\ \text{隐藏状态(Hidden State)} &: \quad h_t = o_t \odot \tanh(C_t) \end{aligned}
遗忘门(Forget Gate)输入门(Input Gate)候选细胞状态(Candidate)细胞状态更新(Cell State)输出门(Output Gate)隐藏状态(Hidden State):ft=σ(Wf⋅[ht−1,xt]+bf):it=σ(Wi⋅[ht−1,xt]+bi):C~t=tanh(WC⋅[ht−1,xt]+bC):Ct=ft⊙Ct−1+it⊙C~t:ot=σ(Wo⋅[ht−1,xt]+bo):ht=ot⊙tanh(Ct)
对于LSTM公式的的符号说明:
- σ \sigma σ:Sigmoid 激活函数
- tanh \tanh tanh:双曲正切激活函数
- W f , W i , W C , W o W_f, W_i, W_C, W_o Wf,Wi,WC,Wo:权重矩阵
- b f , b i , b C , b o b_f, b_i, b_C, b_o bf,bi,bC,bo:偏置向量
- ⊙ \odot ⊙:逐元素乘法(Hadamard 积)
- [ h t − 1 , x t ] [h_{t-1}, x_t] [ht−1,xt]:上一时刻隐藏状态与当前输入的拼接
LSTM计算流程:
- 遗忘门 f t f_t ft 决定从细胞状态中丢弃哪些信息
- 输入门 i t i_t it 和候选状态 C ~ t \tilde{C}_t C~t 共同决定新增信息
- 更新细胞状态 C t C_t Ct
- 输出门 o t o_t ot 控制最终输出的隐藏状态 h t h_t ht
2.2 ConvLSTM的联合建模
ConvLSTM的数学形式彻底重构了LSTM的运算规则。设输入为
X
t
∈
R
H
×
W
×
C
X_t \in \mathbb{R}^{H×W×C}
Xt∈RH×W×C(高×宽×通道),则其核心公式为:
输入门:
i
t
=
σ
(
W
x
i
∗
X
t
+
W
h
i
∗
H
t
−
1
+
b
i
)
遗忘门:
f
t
=
σ
(
W
x
f
∗
X
t
+
W
h
f
∗
H
t
−
1
+
b
f
)
候选状态:
C
~
t
=
tanh
(
W
x
c
∗
X
t
+
W
h
c
∗
H
t
−
1
+
b
c
)
细胞状态:
C
t
=
f
t
∘
C
t
−
1
+
i
t
∘
C
~
t
输出门:
o
t
=
σ
(
W
x
o
∗
X
t
+
W
h
o
∗
H
t
−
1
+
b
o
)
隐藏状态:
H
t
=
o
t
∘
tanh
(
C
t
)
\begin{aligned} \text{输入门: } & i_t = \sigma(W_{xi} * X_t + W_{hi} * H_{t-1} + b_i) \\ \text{遗忘门: } & f_t = \sigma(W_{xf} * X_t + W_{hf} * H_{t-1} + b_f) \\ \text{候选状态: } & \tilde{C}_t = \tanh(W_{xc} * X_t + W_{hc} * H_{t-1} + b_c) \\ \text{细胞状态: } & C_t = f_t \circ C_{t-1} + i_t \circ \tilde{C}_t \\ \text{输出门: } & o_t = \sigma(W_{xo} * X_t + W_{ho} * H_{t-1} + b_o) \\ \text{隐藏状态: } & H_t = o_t \circ \tanh(C_t) \end{aligned}
输入门: 遗忘门: 候选状态: 细胞状态: 输出门: 隐藏状态: it=σ(Wxi∗Xt+Whi∗Ht−1+bi)ft=σ(Wxf∗Xt+Whf∗Ht−1+bf)C~t=tanh(Wxc∗Xt+Whc∗Ht−1+bc)Ct=ft∘Ct−1+it∘C~tot=σ(Wxo∗Xt+Who∗Ht−1+bo)Ht=ot∘tanh(Ct)
其中 ∗ * ∗表示卷积运算, ∘ \circ ∘为逐元素乘。所有中间状态 ( C t , H t ) (C_t, H_t) (Ct,Ht)均保持3D结构,实现时空演化的连续建模。
2.3 核心矛盾:张量坍缩 vs 结构保持
- CNN-LSTM通过展平操作(Flatten)将空间特征压缩为向量,导致空间拓扑关系在时间建模阶段不可逆丢失。例如,图像中的相对位置信息在展平后变为绝对索引,破坏了平移不变性。
- ConvLSTM始终维持张量的空间维度,使得门控机制能感知局部空间上下文。如在降水预测中,卷积核可捕捉相邻区域的湿度梯度变化,而传统LSTM只能处理全局统计特征。
以上是要了解CNN-LSTM与ConvLSTM的区别的背景知识,只是根据目前能看到的blog进行了一个简单的总结。博主没有去看过ConvLSTM的原文,是根据其他博主写的blog去学习ConvLSTM这个模型的,然后在看其他博文的时候有一句话就不是很理解——“ConvLSTM的与LSTM(也叫FC-LSTM,这是为了凸显这两个循环网络计算方式有所不同)区别是全连接层使用卷积计算来代替,也就是矩阵乘法变成了卷积计算。”博主查阅了很多资料,目前将我对这句话的理解尽可能通俗的用大白话讲出来。
三、全连接层使用卷积计算来代替究竟是什么
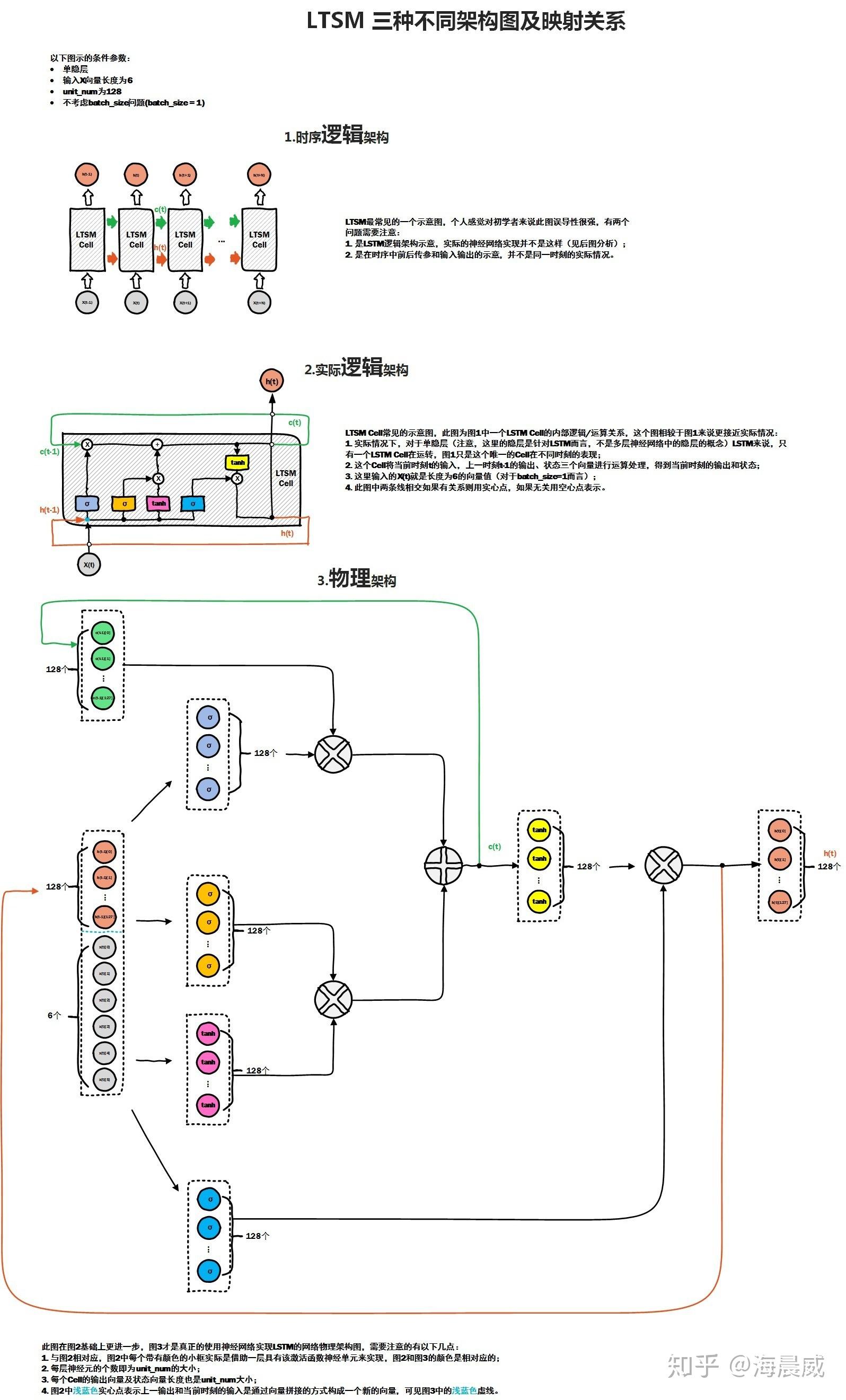
参考海晨威,一幅图真正理解LSTM的物理结构,https://zhuanlan.zhihu.com/p/64613239,LSTM中的每一个门实际上就是一个以sigmoid为激活函数的全连接层(线性层,nn.Linear),就是在图中3.物理架构这部分中,128维的 h t h_t ht与6维的 x t x_t xt拼接(concat)之后变成一个134维的新的向量作为输入,经过那四个箭头(全连接的线性层,nn.Linear(input_dim = 134,output_dim = 128))之后又变成了4个新的128维的向量。
那么为什么对于FC-LSTM这里不能用卷积运算还是只能用线性层来进行信息汇聚呢?因为 LSTM输入数据是sequence,因此不适用于空间+序列这种多了一个维度的数据。因此在CNN-LSTM中,我们是可以用CNN在空间+序列这种类型的数据上做卷积提取信息的,在最后提取出来的信息,我们会回进行一个碾平处理,就是公式(2)里面的flatten,把属于空间的维度磨平之后的数据才可以在FC-LTSM模型里面进行传递,因为它里面要过一个线性层,而线性矩阵只能通过一个二维的表格类型的数据(不考虑batch_size那一个维度),不能够通过图片数据那种有通道数,长,宽三个维度的数据。正是因为线性层接受数据类型的限制,使得CNN-LSTM被迫对空间+序列这种类型的数据上做卷积提取信息后做了一个flatten这种简单粗暴的做法,而ConvLSTM就是针对这一点做法做出了改进,而他的做法就是用卷积算子操作来替换了线性层。具体要用多少个卷积,这都是模型设定的超参数了,属于网络架构了,然后卷积算子的权重一样的都是通过计算出损失函数之后反向传播迭代优化出来的。
四、ConvLSTM代码
代码其实不是很难了,网上已经有很多并且写的挺规范的代码了,现在问deepseek也都能给你写出来,关键是构建模型思路的理解,为什么作者会想到要这样做。具体完整的代码见参考资料4和5
五、参考资料
【信息时代最大的门槛就是信息筛选,因此只列看过好的,并且减少重复内容的出现】
[1].海晨威,一幅图真正理解LSTM的物理结构,https://zhuanlan.zhihu.com/p/64613239
[2].马东什么,cnn+lstm和convlstm的区别,https://zhuanlan.zhihu.com/p/297689933
[3].马东什么,LSTM的物理结构和一些细节,https://zhuanlan.zhihu.com/p/293710437
[4].月来客栈,【深度学习】第8.4节 ConvLSTM模型,https://zhuanlan.zhihu.com/p/675543830(这篇blog提供完整convLSTM的代码,数据集是KTH,一个广泛应用于动作识别和行为分析的计算机视觉数据集)
[5].EAI2,时间序列预测18:ConvLSTM 实现用电量/发电量预测,https://blog.csdn.net/weixin_39653948/article/details/105447616(这篇blog提供了完整convLSTM的代码,数据集家庭用电量,是一个时序预测的数据集)
六、致谢:
图的最初一版是EDU GUO绘制,https://www.zhihu.com/people/edu-guo,予以感谢























 647
647

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








