对于学习计算机图形学的人来说,对其中的几个变换开始时往往有些难以理解。就算理解了,也是一知半解。不过,一般的图形学编程来说,不用深入这些变换照样能够编写程序。有些人学了4、5年图形学,但是还没有完整的推导或者实践一下这几个关键的变换,因为这耗时,而且得沉住气,但往往收获也是巨大的。
前几天,看到Cg的OpenGL examples中有一个“08_vertex_transform”例子,所以的这几个变换都有程序实现,我就决心来深入一下这几个变换。
先要明白两点:
首先,OpenGL采用列向量矩阵,所以几个相应矩阵按照左乘的方式进行,也就是:
最终的投影矩阵 modelViewProj = projectionMatrix * viewMatrix * modelMatrix。modelMatrix中平移、旋转缩放同样符合这种顺序。
第二,对于3D程序来说,一般情况下viewMaxtrix和projectMatrix只需设置一次即可, 产生动画通过变换modelMatrix达到。当然,如果你变换viewMaxtrix,也能达到动画的效果。在gl中采用两个函数gluLookAt和gluPerspective来设置这两个矩阵。
下面来看看这几个变换。
模型变换时最容易理解的,涉及旋转、平移和缩放。在OpenGL中的glRotate,glTranslate和glScale.目前,Cg的这个例子没有完成Scale的变换,我自己写的,很简单。先给出平移和缩放的矩阵构建代码。
static void makeTranslateMatrix(float x, float y, float z, float m[16])
{
m[0] = 1; m[1] = 0; m[2] = 0; m[3] = x;
m[4] = 0; m[5] = 1; m[6] = 0; m[7] = y;
m[8] = 0; m[9] = 0; m[10] = 1; m[11] = z;
m[12] = 0; m[13] = 0; m[14] = 0; m[15] = 1;
}
static void makeScaleMatrix(float ax, float ay, float az, float m[16])
{
m[0] = ax; m[1] = 0; m[2] = 0; m[3] = 0;
m[4] = 0; m[5] = ay; m[6] = 0; m[7] = 0;
m[8] = 0; m[9] = 0; m[10] = az; m[11] = 0;
m[12] = 0; m[13] = 0; m[14] = 0; m[15] = 1;
}
而旋转要复杂一点,因为要考虑任意向量V,当然这个向量是从原点出发的(要是任意轴旋转,轴的端点可以是任意两点)。5个步骤如下:
1. 绕x轴将向量V旋转a角度到xoz平面,记为Tx(a);
2. 绕y轴将向量V旋转b角度到与x轴重合,记为Ty(b);
3. 将物体绕x轴(向量V)旋转θ角度,记为Tx(θ);
4. 2的逆过程,记为Ty(-b);
5. 1的逆过程,记为Tx(-a);
为方便起见,将向量V归一化, 得到Vn(v0,v1,v2)。由此 可知
cosa = v2/sqrt(v1^2+v2^2);
cosb = v0;
再加这个Tx(a)变换,其他类似:
x′=x
y′=ycosθ-zsinθ
z′=ysinθ+zcosθ
这些信息都清楚了,何不手工算一下这个旋转矩阵呢?多准备一点草稿纸,肯定能得出最后结果。旋转变换矩阵有些麻烦,直接给代码:
static void makeRotateMatrix(float angle, float ax, float ay, float az,float m[16])
{
float radians, sine, cosine, ab, bc, ca, tx, ty, tz;
float axis[3];
float mag;
axis[0] = ax;
axis[1] = ay;
axis[2] = az;
mag = sqrt(axis[0]*axis[0] + axis[1]*axis[1] + axis[2]*axis[2]);
if (mag)
{
axis[0] /= mag;
axis[1] /= mag;
axis[2] /= mag;
}
//normalizing above
radians = angle * myPi / 180.0;
sine = sin(radians);
cosine = cos(radians);
ab = axis[0] * axis[1] * (1 - cosine);
bc = axis[1] * axis[2] * (1 - cosine);
ca = axis[2] * axis[0] * (1 - cosine);
tx = axis[0] * axis[0];
ty = axis[1] * axis[1];
tz = axis[2] * axis[2];
m[0] = tx + cosine * (1 - tx);
m[1] = ab + axis[2] * sine;
m[2] = ca - axis[1] * sine;
m[3] = 0.0f;
m[4] = ab - axis[2] * sine;
m[5] = ty + cosine * (1 - ty);
m[6] = bc + axis[0] * sine;
m[7] = 0.0f;
m[8] = ca + axis[1] * sine;
m[9] = bc - axis[0] * sine;
m[10] = tz + cosine * (1 - tz);
m[11] = 0;
m[12] = 0;
m[13] = 0;
m[14] = 0;
m[15] = 1;
}
至此,模型变换已完成。
接下来来看viewMatrix。
视图变换实际上是坐标系的变换,将世界坐标系变换到眼坐标系(view ),这样做可以方便后面的投影(Projection)操作,因为投影是在眼坐标系中进行的。
建立眼坐标系用gluLookAt函数来实现,我们看看函数原型:
gluLookAt(double eyex, double eyey, double eyez, double centerx, double centery, double centerz, double upx, double upy, double upz)
这些参数中包括三种信息:眼睛的位置eye,视点中心位置center和向上的向量up。注意up不是y轴,只是指明了y轴的大致方向。
设眼睛的位置为原点,向量(eye-center)所得的向量为Z轴,y叉乘z得到x轴,再由x轴和z轴叉乘,反算出y轴。这就是眼坐标系的三个方向,设其单位向量为u、v、n。
然后就是坐标系之间的变换,这一点可以通过两种思路来完成:
1. 将眼坐标系变换到同世界坐标系重合。
2.代数的方法。
对于1而言,又有两种思路:
1. 代数上已经证明的公式:先移动eye的位置到世界坐标系的原点,再进行正交变换;
2. 由基本的变换合成,如下:
1)移动眼睛的位置到世界坐标系原点;
2)将眼坐标系绕世界坐标系x轴旋转,使得眼坐标系的z轴位于世界坐标系xoz平面;
3)将眼坐标系绕世界坐标系y轴旋转,使得眼坐标系的z轴和世界坐标系z轴重合;
4)将眼坐标系绕世界坐标系z轴旋转,使得眼坐标系的x、y轴和世界坐标系x、y轴重合;
这个步骤也需要很多的草稿纸,O(∩_∩)O
对于2,代数的方法,显得更简洁一些,看下图: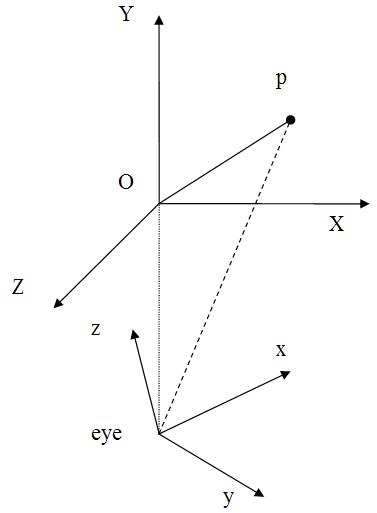
图中,对于任意的P点,向量减OP-Oeye= eyeP。再考虑eyeP向量,将其对眼坐标系的x/y/z轴进行投影,呵呵,就能得到P点在新坐标系中的坐标。投影很简单,用点乘即可。
于是,对于P点的新坐标P'(x',y',z'):
x' =(OP-Oeye).u = OP.u - Oeye.u =(x,y,z).(u[0],u[1],u[2]) -Oeye.(u[0],u[1],u[2]);
其中,u为眼坐标x轴方向的单位向量, x为P点的x坐标,u[0]为u向量的x值;其他类似。
y、z类似,我想你应该能写出矩阵来了吧,此处矩阵略过,直接看代码吧。
/* Build a row-major (C-style) 4x4 matrix transform based on the parameters for gluLookAt. */
static void buildLookAtMatrix(double eyex, double eyey, double eyez,
double centerx, double centery, double centerz,
double upx, double upy, double upz,float m[16])
{
double x[3], y[3], z[3], mag;
/* Difference eye and center vectors to make Z vector. */
z[0] = eyex - centerx;
z[1] = eyey - centery;
z[2] = eyez - centerz;
/* Normalize Z. */
mag = sqrt(z[0]*z[0] + z[1]*z[1] + z[2]*z[2]);
if (mag) {
z[0] /= mag;
z[1] /= mag;
z[2] /= mag;
}
/* Up vector makes Y vector. */
y[0] = upx;
y[1] = upy;
y[2] = upz;
/* X vector = Y cross Z. */
x[0] = y[1]*z[2] - y[2]*z[1];
x[1] = -y[0]*z[2] + y[2]*z[0];
x[2] = y[0]*z[1] - y[1]*z[0];
/* Recompute Y = Z cross X. */
y[0] = z[1]*x[2] - z[2]*x[1];
y[1] = -z[0]*x[2] + z[2]*x[0];
y[2] = z[0]*x[1] - z[1]*x[0];
/* Normalize X. */
mag = sqrt(x[0]*x[0] + x[1]*x[1] + x[2]*x[2]);
if (mag) {
x[0] /= mag;
x[1] /= mag;
x[2] /= mag;
}
/* Normalize Y. */
mag = sqrt(y[0]*y[0] + y[1]*y[1] + y[2]*y[2]);
if (mag) {
y[0] /= mag;
y[1] /= mag;
y[2] /= mag;
}
/* Build resulting view matrix. */
m[0*4+0] = x[0]; m[0*4+1] = x[1];
m[0*4+2] = x[2]; m[0*4+3] = -x[0]*eyex + -x[1]*eyey + -x[2]*eyez;
m[1*4+0] = y[0]; m[1*4+1] = y[1];
m[1*4+2] = y[2]; m[1*4+3] = -y[0]*eyex + -y[1]*eyey + -y[2]*eyez;
m[2*4+0] = z[0]; m[2*4+1] = z[1];
m[2*4+2] = z[2]; m[2*4+3] = -z[0]*eyex + -z[1]*eyey + -z[2]*eyez;
m[3*4+0] = 0.0; m[3*4+1] = 0.0; m[3*4+2] = 0.0; m[3*4+3] = 1.0;
}
到此,view矩阵已经OK了。






















 457
457

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








