电机物理数学建模

电机定义

电机是以磁场为媒介，利用电磁感应作用进行能量转换与传递的电磁装置。
机电能量转换装置，无论尺寸大小，从大型旋转电机如水轮发电机到小型机电信号变换器，虽然它们的用途和结构各异，但都基于相同的电磁场与运动载电物体（通常是载流导体）相互作用的基本原理。在机电装置中，当可动部分发生位移，导致装置内部耦合电磁场的储能发生变化时，通过耦合场的作用，电能与机械能之间可以相互转换。因此，机电能量转换装置通常包含载流的电系统（如绕组）、机械系统以及用作耦合和储存能量的电磁场，它们由一个固定部分和一个可动部分组成。机电能量转换是一个可逆的过程，这意味着大多数发电机可以作为电动机运行，反之亦然。

电机发展史

电机发展的历史，大体上可以分成 三个时期:
(1)直流电机的产生和形成时期;
(2)交流电机的形成和发展时期;
(3)电机理论、设计和制造 工艺逐步达到完善化的时期。

直流电机的产生和形成时期

1. 1821年 - 法拉第发现载流导体在磁场内受力的现象。
2. 1831年 - 法拉第发现电磁感应定律。
3. 1833年 - 楞茨证明电机的可逆原理。
4. 1834年 - 直流发电机开始发展，满足生产需要。
5. 1870年 - 直流发电机和电动机的可逆原理被接受，发展合而为一。
6. 1873年 - 海夫纳-阿尔泰涅克发明鼓形电枢绕组。
7. 1880年 - 爱迪生提出采用叠片铁心。
8. 1882年 - 台勃莱兹成功进行长距离直流电输送实验。
9. 1884年 - 出现换向极和补偿绕组。
10. 1885年 - 开始使用炭粉电刷。
11. 1886年 - 雀普金生兄弟确立磁路的欧姆定律。
12. 1891年 - 阿尔诺德建立直流电枢绕组理论。
13.19世纪末 - 直流电机具备了现代直流电机的主要结构特点，人们开始关注交流电

交流电机的形成和发展时期

1832年 - 单相交流发电机出现
1876年 - 亚勃罗契柯夫首次采用交流和开磁路式变压器给“电烛”供电
1884年 - 霍普金生兄弟发明了具有闭合磁路的变压器
1885年 - 齐波诺斯基、德利和勃拉第提出了变压器的芯式和壳式结构
1885年 - 弗拉利斯制成了第一台两相感应电动机
1888年 - 弗拉利斯提出了“利用交流电来产生电动旋转”的经典论文
1889年 - 多利伏-多勃罗伏尔斯基提出了三相制的建议，并设计和制出了三相感应电动机
1891年 - 建成了从劳芬到法兰克福的三相电力系统，显示三相交流电的优越性
1893年 - 开耐菜和司坦麦茨开始用复数和相量来分析交流电路
1894年 - 海兰特发表了“多相感应电动机和变压器性能的图解确定法”的论文
1894年 - 弗拉利斯采用双旋转磁场理论来分析单相感应电动机
1894年 - 波梯建立了交轴磁场理论
1899年 - 布朗台尔提出了双反应理论
19世纪末 - 各种交、直流电机的基本类型及其基本理论和设计方法大体上都已建立起来

电机理论、设计和制造工艺逐步达到完善化时期

20世纪初 - 水轮发电机的最大单机容量不超过1000kW，汽轮发电机的单机容量不超过500kW
1918年 - 福提斯古提出了求解三相不对称问题的一般方法——对称分量法
1926-1930年 - 道赫提和聂克尔在发展勃朗台尔双反应理论的基础上，发表了五篇经典论文
1929年 - 派克发表了“同步电机的双反应理论(1)—通用分析方法”的经典论文
1935-1938年 - 克朗提出了原型电机的概念，并利用张量分析来研究旋转电机
1920-1940年间 - 许多学者对双笼和深槽电机的理论和计算方法，谐波磁场所产生的寄生转矩及其削弱，感应电机的噪声等问题进行了一系列的研究
20世纪40年代前后 - 出现了一系列的控制电机，如电机放大器、交流测速发电机、旋转变压器等
1954年 - 柯伐煦提出了空间矢量法，并导出了感应电机的空间矢量电压方程
1957-1969年 - 卡佐夫斯基发表了一系列论文，提出用频率法来分析和求解交流电机的各种瞬态过程和非正常运行情况
1965年以后 - 计算机逐步被引入到电机工程的各个领域，先是模拟计算机，然后是数字计算机
1971年 - 勃拉舒克和海斯提出了交流电机的“矢量变换控制”
20世纪70年代以后 - 大电流晶闸管的发展，出现了便于控制、体积小、噪声小的大容量直流电源
20世纪80年代以后 - 永磁无刷电机和开关磁阻电机等新型电机得到较快的发展
20世纪90年代以后 - 一种场路结合的有限元一状态空间耦合时步法得到应用
20世纪末 - 电机理论和设计方法持续发展，计算机技术的进步使得电机的动态分析和设计更加精确。

电机学习框架

1. 建立物理模型：
   • 首先，了解电机的基本结构和主要部件的功能。
   • 分析电机的磁路和电路。
   • 研究空载和负载条件下电机内部的磁场、绕组中的电动势以及作用在转子上的电磁转矩。
   • 初步掌握电机的工作原理。
2. 建立数学模型：
   • 导出电机的运动方程，包括磁动势方程（或磁链方程）、电压方程和转矩方程。
   • 利用电磁学和动力学的基本定律，将电机内部的电磁过程和机电过程，用数学方程形式表达出来。
   • 这一步的目的是建立电机的数学模型，以便进行进一步的分析和计算。
3. 求解运动方程：
   • 根据问题的具体情况（如稳态、瞬态、对称或不对称运行等），确定合适的解法。
   • 求解运动方程可以采用解析解或数值解的方法，具体取决于问题的复杂性和可用的计算工具。
4. 结果分析：
   • 对求解结果进行分析，以确定电机的各种运行性能和主要运行数据。
   • 分析电机的额定数据、过载能力、稳定性、效率、电压变化率或速度变化率等性能指标。
   • 这一步的目的是满足解决日常工程问题的需要，并根据分析结果对电机的设计和运行进行优化。

以上四个步骤构成了电机学习的基本方法和框架，通过这些步骤，可以深入理解电机的工作原理、分析其性能，并解决实际工程中的问题。

理想电机能力模型

机电能量转换过程
机电能量转换过程是电场和磁场与运动的载电物体（通常为载流导体）相互作用的结果。当机电装置的可动部分发生位移，使装置内部耦合电磁场的储能发生变化，并在与之连接的电路系统和机械系统内产生一定的反应时，通过耦合场的作用，电能就会转换成机械能或反之。
机电能量转换装置的组成部分

1. 载流的电系统（绕组）：用于产生和传输电流。
2. 机械系统：用于产生和传递机械能。
3. 电磁场：用作耦合和储存能量的介质。

机电能量转换的特点

• 可逆性：大多数发电机可以作为电动机运行，反之亦然。
• 固定部分和可动部分：机电能量转换装置通常由固定部分和可动部分组成。

机电能量转换过程是电能和机械能之间相互转换的过程，它依赖于载流导体、机械系统和电磁场之间的相互作用。这种转换过程是可逆的，使得发电机和电动机在特定条件下可以互换使用。
绝大多数旋转电机都由电系统、机械系统和联系两者的耦合电磁场组成。其中电系统主要指定、转子绕组，绕组的出线端就是系统的电端又;机械系统主要指电机的转子，转轴则是系统的机械端又;耦合场可以是磁场，也可以是电场。考虑到在正常磁通密度和电场强度 下，单位体积内磁场的储能密度要比电场的储能密度大得多，所以绝大多数电机都以磁场作为耦合场。

把电机作为一个具有电端又和机械端又的两端又装置，并把电阻损耗:$i^{2}R$从电系统中移出，其中R为绕组的电阻:转子的机械损耗${\Omega }^2{R}_{\Omega }$。从机械系统中移出，其中R。为机械阻力 系数;再把铁心损耗忽略不计;则装置的中心部分将成为 一个由无铁耗的铁心、气隙和无铜 粍、无机械损耗的动态耦合电路所组成的“无损耗的磁储能系统”。
电机能量模型可知，包括几个部分：
1.电能输入
2.感应电动势
3.磁能存储
4.电磁转矩
5.机械能输出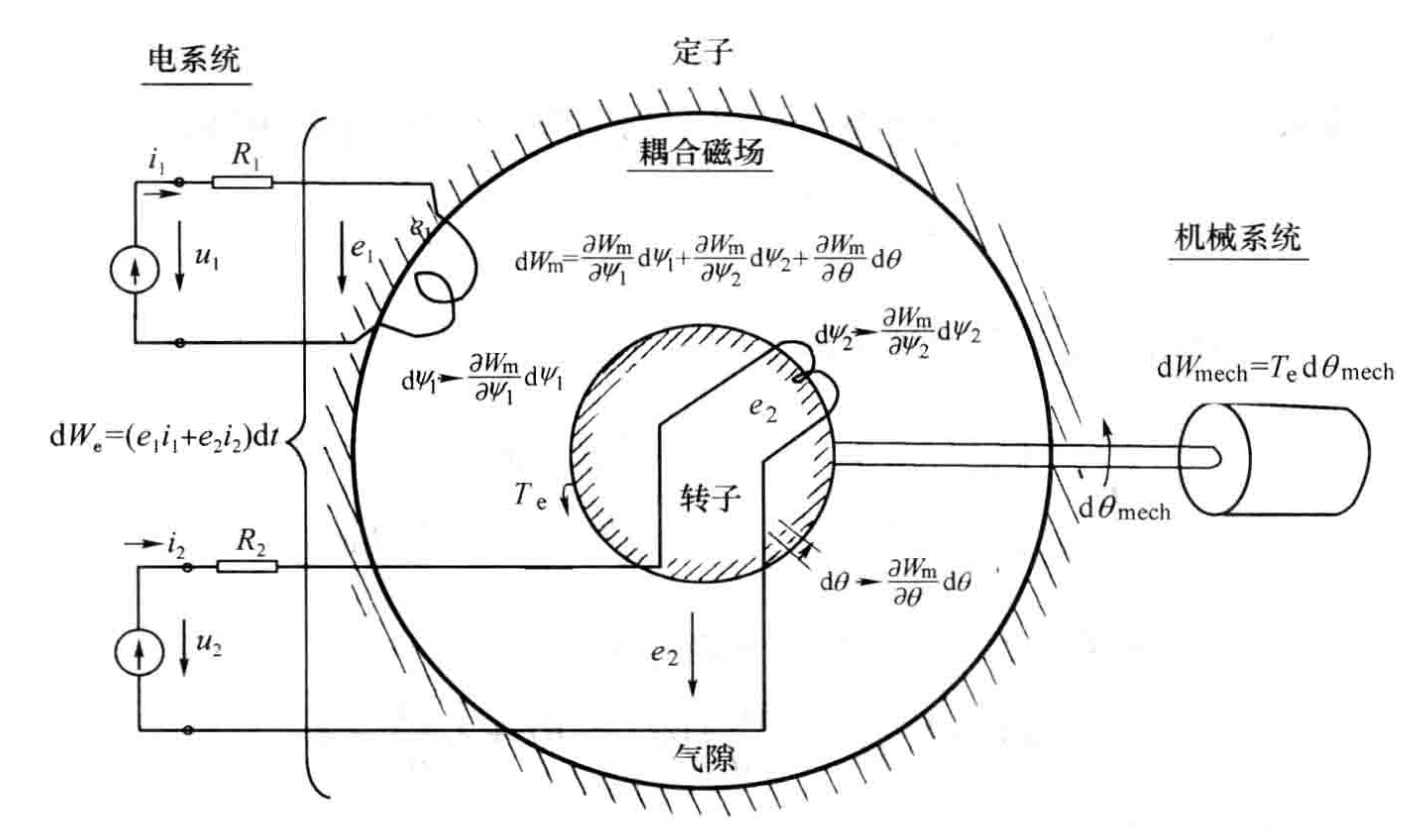

能量转换过程：
1.机电能量转化方程
2.电路方程
3.磁路方程
4.电磁转矩方程

转动电磁装置模型

单激励机电装置

该装置由定子铁心、转子铁心和气隙组成一个闭电源合磁路，定 子铁心上装有一个绕组，该绕组与电源相连接，转子为凸极、不装绕组。这种装置的气隙主磁场 (耦合场)由定子电流所产生的磁动势单独激励而形成，故称为单激励装置。
电能输入
耦合场的磁场发生变化时，耦合场将对定子电路作出反应。设定子绕组的磁链为$\Psi$， 根据法拉第电磁感应定律，$\Psi$的变化将在定子绕组内感生电动势e
$e=\frac{d\Psi }{dt}$
在时间dt内，电源向电系统输人的微分净电能dwe
$$\begin{gathered} d{W}_e=(u-iR)idt \\ u-iR=-e,e=-\frac{d\Psi }{dt} \\ d{W}_e=-eidt=id\Psi \end{gathered}$$
机械能输出
$$\begin{gathered} d{W}_{mech}=(T_{mech}+R_{\Omega }\Omega )d\theta =T_{e}d{\theta }_{mech} \\ {T}_e=T_{mech}+R_{\Omega }\Omega \end{gathered}$$**磁场储能
$$\begin{gathered} d{W}_m=d{W}_e-d{W}_{mech}=id\Psi -T_{e}d{\theta }_{mech} \\ d{W}_m(\Psi ,\theta )=id\Psi -\frac{1}{p}{T}_{e}d\theta \\ \theta 是电角，和转角关系为：\theta =p{\theta }_{mech} \end{gathered}$$
磁能$W_m$是磁链$\Psi$和转角$\theta$两者的函数，即$W_m=W_m(\Psi ,\theta )$。所以从理论上 讲，如果已知电流i与磁链$\Psi$和转角$\theta$两者的关系$i(\Psi ,\theta )$，以及电磁转矩$T_e$与磁链$\Psi$和转角$\theta$两者的关系$T_e(\Psi ,\theta )$ 通 过 上 式 进 行 积 分 ， 即 可 求 出 磁链$\Psi$和转角的 终 值 达 到 磁链${\Psi }_0$和转角${\theta }_0$时 ， 耦 合 场 的 磁 能 $W_m({\Psi }_0,{\theta }_0)$， 即
$W_m({\Psi }_0,{\theta }_0)={\int }_{\Psi =0,\theta =0}^{{\Psi }_0,{\theta }_0}[i(\Psi ,\theta )d\Psi -\frac{1}{p}{T}_e(\Psi ,\theta )d\theta ]$
若磁路为线性，$\Psi -i$曲线是一条直线，$\Psi =L(\theta )i$,其中$L(\theta )$为定子绕组的自感，它仅是转角$\theta$的函数，此时$i=\Psi /L(\theta )$,于是
$$\begin{gathered} W_m(\Psi ,\theta )={\int }_0^{\Psi }i({\Psi }^{{}^{\prime }},\theta )d{\Psi }^{{}^{\prime }}={\int }_0^{\Psi }\frac{{\Psi }^{{}^{\prime }}}{L(\theta )}d{\Psi }^{{}^{\prime }}=\frac{1}{2}\frac{{\Psi }^2}{L(\theta )} \\ {W}_m(i,\theta )=\frac{1}{2}L(\theta )i^2 \end{gathered}$$
**电磁转矩 **
由于磁能$W_m$是磁链 $\psi$和转角$\theta$的函数，即$W_m=W_m(\psi ,\theta )$，所以磁能的全微分$d{W}_m$应为
$d{W}_m(\psi ,\theta )=\frac{\partial W_m}{\partial \psi }d\psi +\frac{\partial W_m}{\partial \theta }d\theta$
另一方面，
$d{W}_m(\psi ,\theta )=id\psi -T_{m}d\theta$
磁链 $\psi$和转角$\theta$是独立变量所以：
$i=\frac{\partial W_m(\psi ,\theta )}{\partial \psi }$
电磁转矩对应为：
$T_e=\frac{\partial W_m(\psi ,\theta )}{\partial {\theta }_{mech}}=-p\frac{\partial W_m(\psi ,\theta )}{\partial \theta }$
上式就是用系统的磁能表示时，电磁转矩的表达式。
当转子做微笑的角位移（可以使实际角位移，也可以使设想的虚角位移），如果系统的磁能同时发生变化，则转子上将受到电磁转矩的作用。电磁转矩的值等一磁能对转角的偏导数$\frac{\partial W_m(\psi ,\theta )}{\partial {\theta }_{mech}}$（磁链约束为常值），电磁转矩的方向为在恒磁链下趋势磁能减小的方向。
对于磁能为线性的情况，由于$W_m=\frac{1}{2}\frac{{\psi }^2}{L(\theta )}$，故用磁链$\psi$和转角$\theta$表示时，电磁转矩$T_e$应为
$T_e=-p\frac{\partial }{\partial \theta }(\frac{1}{2}\frac{{\psi }^2}{L(\theta )})=\frac{1}{2}p\frac{{\psi }^2}{L(\theta {)}^2}\frac{\partial L(\theta )}{\partial \theta }$
用电流和转角表示时也可以写成：
$T_e=\frac{1}{2}$