源自:系统工程与电子技术
作者:吴冯国 陶伟 李辉 张建伟 郑成辰.
“人工智能技术与咨询” 发布
摘 要
为提升无人机在复杂空战场景中的存活率, 基于公开无人机空战博弈仿真平台, 使用强化学习方法生成机动策略, 以深度双Q网络(double deep Q-network, DDQN)和深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法为基础, 提出单元状态序列(unit state sequence, USS), 并采用门控循环单元(gated recurrent unit, GRU)融合USS中的态势特征, 增加复杂空战场景下的状态特征识别能力和算法收敛能力。实验结果表明, 智能体在面对采用标准比例导引算法的导弹攻击时, 取得了98%的规避导弹存活率, 使无人机在多发导弹同时攻击的复杂场景中, 也能够取得88%的存活率, 对比传统的简单机动模式, 无人机的存活率大幅提高。
关键词
深度强化学习 ; 无人机 ; 单元状态序列 ; 门控循环单元
引言
现代空战环境错综复杂, 空空导弹和机载雷达性能不断提升, 超视距空战已经在现代空战中占据主导地位[1], 空空导弹也早已成为打击空中单位的主要武器。无人机作为空中战场的理想作战目标之一, 被普遍运用到军事领域当中[2]。利用无人机可持续大机动的飞行特点, 采取高效的机动策略以提高无人机对导弹的规避、逃逸成功率, 对提升无人机的空战生存能力而言至关重要[3]。
无人机规避空空导弹问题一直都是空战的研究热点。王怀威等[4]采用蒙特卡罗方法验证了无人机实施常规盘旋机动规避导弹的效果。Imado等[5]利用微分对策法研究导弹与无人机差速博弈的问题。另外, 还有诸多针对导弹的规避方式[6-10]、规避效能评估[11-13]以及无人机最优或次优规避策略解析解[14-16]等方面的研究。以上方法依赖于完备的空战对战模型以求解在单枚导弹打击情况下的最优机动策略, 当导弹数量变化时, 模型很难理解, 而且建立空战对战模型本身就是一个非常复杂的过程, 需要使用大量微分函数结合积分函数,才能表征无人机与导弹状态属性的转移规律。
深度强化学习(deep reinforcement learning, DRL)算法在马尔可夫决策过程(Markov decision process, MDP)基础上, 采用端到端学习方式, 以态势信息为输入, 直接利用神经网络获取输出, 控制智能体作出决策, 被广泛应用于自动化控制当中[17-22]。范鑫磊等[23]将深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法[24]应用于无人机规避导弹训练, 在简易模型下对固定态势攻击的空空导弹进行仿真验证。宋宏川等[25]针对导弹制导规则设计成型奖励, 用DDPG算法训练无人机规避正面来袭的导弹, 对比典型规避策略, 训练出了仅次于置尾下降机动的逃逸策略。
上述研究表明, 无人机能够通过特定的机动方式来规避空空导弹的打击, 而深度强化学习算法可以训练出自动规避空空导弹的智能体。总体而言, 以往研究大多基于单枚导弹打击场景。但是在超视距空战中, 多枚导弹从不同方向锁定无人机并发动协同攻击的情况屡见不鲜。在这种情形下, DRL算法会存在状态空间维度大, 状态信息维度不断变化, 神经网络输入维度难以固定, 算法收敛性能差等问题。
针对以上问题, 本文提出一种基于单元状态序列(unit state sequence, USS)的强化学习算法(reinforcement learning method based on USS, SSRL)。在该算法中,首先,将导弹和无人机进行一对一的特征编码,形成特征单元; 其次,根据距离优先级对所有编码后的特征单元进行排序, 组合成一个USS; 然后,使用门控循环单元(gated recurrent unit, GRU)对USS中的特征单元进行特征融合, 提取其中的隐藏特征信息; 最后,将隐藏特征信息看作该时刻的状态信息,并将信息传入强化学习算法的神经网络。将该算法分别应用于深度双Q网络(double deep Q-network, DDQN)[26]和DDPG算法上, 在公开无人机空战博弈仿真平台上进行训练。仿真结果表明, 由SSRL算法训练的智能体能够学到连续规避机动策略, 控制无人机进行规避导弹机动, 增加导弹脱靶量, 提升无人机连续规避导弹的成功率。
1 相关理论
1.1 MDP
强化学习训练过程类似于人类学习, 即智能体在不断探索和获取外界反馈中学习能够获得的最大利益, 通常被建模成MDP[27]。MDP由状态空间S、动作空间A、状态转移函数P和奖励函数R组成:状态空间是所有可能的状态集合; 动作空间是所有可能的动作集合; 状态转移函数则描述了在当前状态下采取某个动作后到达下一个状态的概率;奖励函数用于描述在当前状态下采取该行动所获得的奖励[28]。
1.2 DDQN算法
强化学习任务通常是时间序列决策问题, 与训练数据高度相关。文献[29]引入经验重放机制, 降低数据之间的相关性, 使样本可重复利用, 提高学习效率。DDQN算法使用两个神经网络,将动作选择和值函数估计进行解耦, 评估网络Q用于环境交互, 用于动作选择的公式如下:
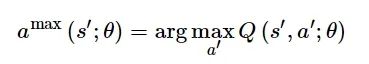
(1)
目标网络Q′用于估计下个状态值函数, 通过最小化损失函数, 更新评估网络参数, 使训练过程更加稳定:
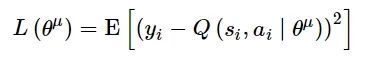
(2)
式中: yi代表目标值, 即:
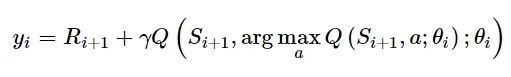
1.3 DDPG算法
DDPG算法基于确定性策略梯度[30](deterministic policy gradient, DPG)算法, 并将DDQN中的双重网络机制应用到ActorCritic框架, 分别使用参数为θμ、θμ′、θQ和θQ′的深度神经网络拟合策略评估函数μ、策略目标函数μ′、动作值评估函数Q和动作值目标函数Q′。
策略评估函数负责与环境交互, 从环境中获取状态S、奖励r、结束标识d, 进行动作选择如下:
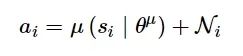
(3)
式中: Ni 为动作噪声, 对噪声使用模拟退火[31]以避免陷入局部最优, 同时增加了算法的探索能力。
智能体通过最小化损失公式,以更新值评估网络参数:
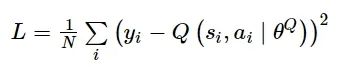
(4)
式中: yi为目标动作值。即:
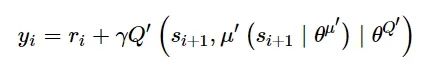
(5)
根据DPG算法的理论证明策略函数关于θμ的梯度等价于动作值函数关于Q(s, a|θQ)的期望梯度, 使得可以以梯度更新策略评估网络:








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1329
1329

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








