最近复习一下之前看的深度学习的网络,在deeplearning-toolbox中看到一个CAE一时没想起来就看了一下官方的解释
CAE(Convolutional Auto-Encode) 卷积自编码 ,对于这个深度学习的网络的的解释很少。
下面谈一下自己的认识,算是总结吧
CAE(Convolutional Auto-Encode) 卷积自编码 :一种卷积自编码器,其实现的过程与Auto-Encode的思想是一致的
都是使用的是先编码在解码,比较解码的数据与原始的数据的差异进行训练,最后得到比较稳定的参数,待这一层的参数都训练好的时,再进行下一个的训练
如此堆积起来的网络看作是Stacked Auto-Encode 为了增加其抗干扰的能力,有时在训练时加入随机噪声进而增加其鲁棒性,称为Stacked denoise Auto-Encode。
但是今天要介绍的CAE只是加入了卷积的训练。其中主要思想是加入一些卷积的操作
1.CAE-UP 可以看做是卷积的的操作(在图像中进行卷积计算,得到卷积的图像)
2.CAE-Down 可以看做是一种翻卷的过程(在上层的基础之上,进行反卷积,得到原始的数据(肯定会有差距))
3.CAE-BP 可以看做是反向椽笔算法来计算残差,损失,计算出梯度与变化值。使用残差值对网络的参数进行更新。
主要的步骤就是这些,剩下的就是堆在一起了。
下面介绍一下在CAE中的数学计算
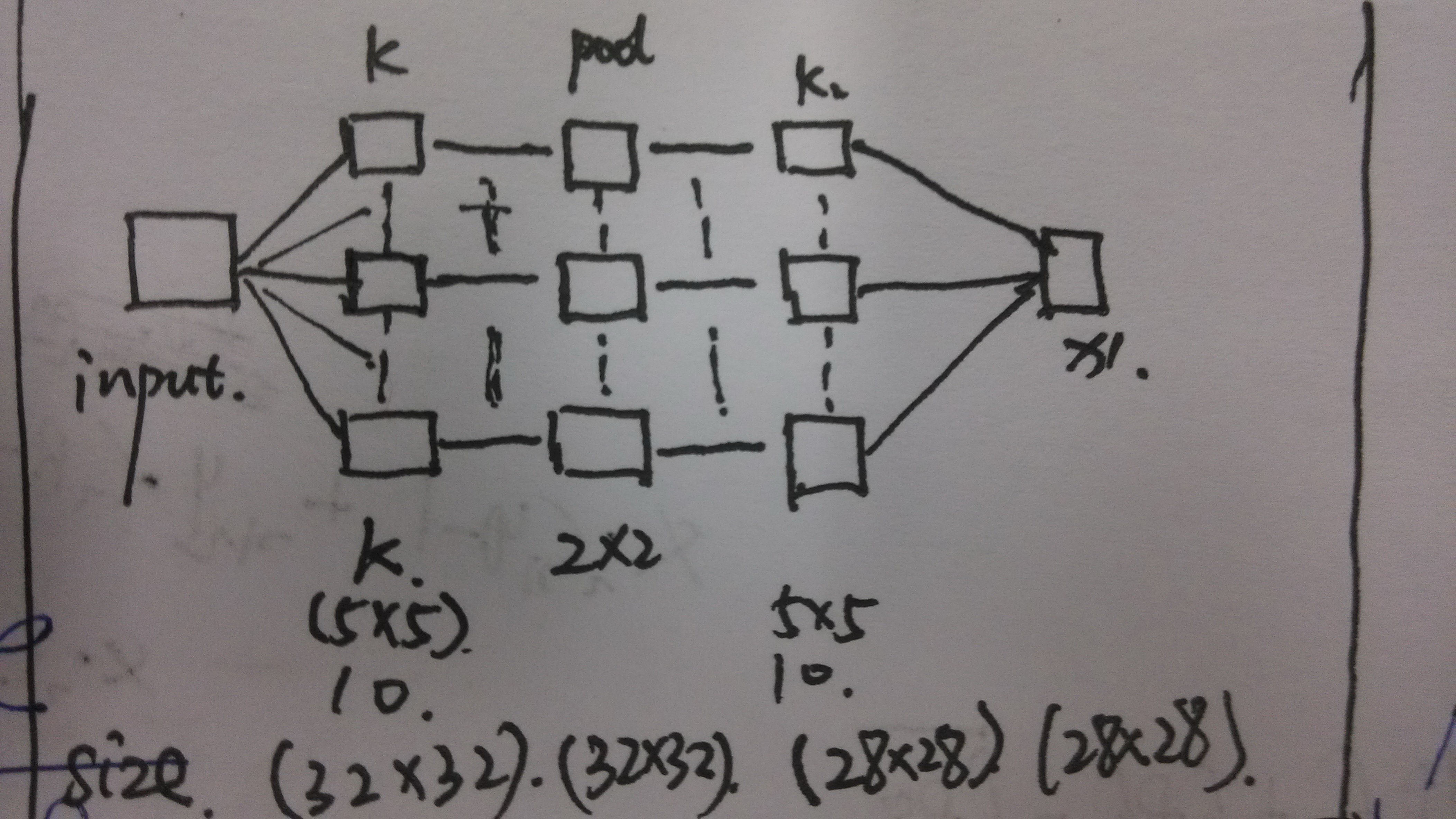
卷积层-卷积:初始化k个卷积核(W),每个卷积核搭配一个偏置b,与输入x卷积( ∗ )后生成k个特征图h,激活函数 σ 是 tanh 。公式如下:
池化层-池化操作(Max Pooling): 对上面生成的特征图进行池化操作,时要保留池化时的位置关系的矩阵,方便之后反池化的操作。
池化层-自编码(反池化操作): 对上面生成的特征图进行反池化操作,用到保留池化时的位置关系的矩阵,将数据还原到原始大小的矩阵的相应的位置(在此可以参考卷积神经网络的一些过程)。
卷积层-自编码(反卷积的操作):每张特征图h与其对应的卷积核的转置 进行卷积操作并将结果求和,然后加上偏置c,激活函数
σ
仍然是
tanh
。公式如下:
卷积层-更新权值:要更新权值,首先要确定cost function,此处作者采用的MSE(最小均方差)函数,即:目标值减去实际值的平方和再求均值,2n是为了简化求导。其中
θ是关于W和b的函数
。公式如下:
但是会存在一种输入要与输出的维度一样才可以进行残差的计算,这个时候,就要对卷积的三种方式就要理清楚是怎样的操作的
卷积的三种操作: 假设原始图像的size是AxA的 卷积核的大小BxB 在计算时候对于边界如果需要进行边界补零操作
1.valid 得到的图像是 (A-B+1)x(A-B+1)
2.full 得到的图像是 (A+B-1)x(A+B-1)
3.same 得到的图像是 AxA
确定好cost function以后,就是对W和b求导,公式如下:
由于论文没有具体给出的
在此参考一下deeplearning-toolbox中的CAE的代码中,其对于卷积使用的full操作,而在进行down时使用的是valid,
这样就是的输入前与输入后保持一致的维度了。
caesdlm是进行梯度检测的
可以进行pooling 也可以选择不使用,只是用来减少参数的,其在计算中只是随机的将某些数据值置为0.
Max pooling:引入Max pooling下采样技术,获取到特征的平移不变性。Max pooling就是pooling时选取最大值。由于采用了pooling技术,因此就没有必须使用L1/L2规则化项了。
文中的实验结果
将上述卷积层和pooling层堆积起来,形成CAEs,最后加入SVMs或其他的分类器。据实验结果显示,CAEs在泛化性、鲁棒性方面表现特别好,尤其是在无监督训练界。
下面补充一下在DeepLearning-toolbox中的CAE的关键代码的解释:
1。caeexamples.m 入口
scae = {
struct('outputmaps', 10, 'inputkernel', [1 5 5], 'outputkernel', [1 5 5], 'scale', [1 2 2], 'sigma', 0.1, 'momentum', 0.9, 'noise', 0)
};
用来定义cae的结构 outputmap 可以理解为卷积核的个数,inputkernel 卷积核的大小,scale池化的窗口大小。noise是否添加噪声
sigma在代码中没有用到(估计是用来计算更新学习率的参考caffe),momentum是用来对原始权重的保留权重。
2。 scaesetup网络参数初始化设置
cae = cae{l};
ll= [opts.batchsize size(x{1}, 2) size(x{1}, 3)] + cae.inputkernel - 1; %size A+k-1 full
X = zeros(ll); %init size
cae.M = nbmap(X, cae.scale);%1*4*256
bounds = cae.outputmaps * prod(cae.inputkernel) + numel(x) * prod(cae.outputkernel);% bounds 275
ll是存放的是卷积之后的图像的尺寸(这里使用的full是对图像进行增大的一种,感觉作者这样写是为了提取图像边缘的数据)
X是进行初始矩阵。cae.M是将图像的scale的大小进行分组列化,图像此时是32*32的,但是在池化时把4个像素点看做一组进行列化(4*256=32*32)的图像方便后面进行池化操作。
bounds的作用是进行卷积的初始化的操作,(本人不是很明白为什么要用这个)
cae.edgemask = zeros([opts.batchsize size(x{1}, 2) size(x{1}, 3)]);% 1*28*28
cae.edgemask(ss(1) : end - ss(1) + 1, ...
ss(2) : end - ss(2) + 1, ...
ss(3) : end - ss(3) + 1) = 1; % 20*20 个有效的作用
这个的操作是对28*28的矩阵中间的20*20的部分进行初始化为1,其他的是0
但是这样是为什么,难道只是把中间的20*20的元素看作是主要的影响银子吗。(这一点不明白)
3。caetrain 训练
cae = caeup(cae, x1); %主要是进行卷积和maxpooling
cae = caedown(cae); %主要是进行反卷积还原图像
cae = caebp(cae, x2); %反向传播计算残差和权重的变化量
cae = caesdlm(cae, opts, m); %进行梯度检验
cae = caeapplygrads(cae); %梯度及偏置参数的更新
4。function X = max3d(X, M)
ll = size(X);
B=X(M);
B=B+rand(size(B))*1e-12;
B=(B.*(B==repmat(max(B,[],2),[1 size(B,2) 1])));
X(M) = B;
reshape(X,ll);
end
% compute reshape 4*256=32*32
% 把图片分成4个像素一组,总共256组,
% 在计算时 取出每一组的最大值即完成最大池化
% 得到一个[0 1]的mask矩阵,然后与B进行相乘
% 可以的得到一个池化后的矩阵
其他的在此就不做解释了,可以参考卷积神经网络的计算。
代码的作者使用的对图像进行扩大的计算来最大可能的保留图像。
参考文献
[1]: Stacked Convolutional Auto-Encoders for Hierarchical Feature Extraction








 本文深入探讨了卷积自编码器(CAE)的概念、数学计算及其在深度学习网络中的应用。重点介绍了CAE的工作原理、关键数学公式以及在DeepLearning-toolbox中的实现细节,包括卷积、池化、反卷积操作及其对网络参数的更新策略。此外,文章还阐述了CAE在网络结构中的堆叠应用、实验结果及其在泛化性和鲁棒性方面的优势。
本文深入探讨了卷积自编码器(CAE)的概念、数学计算及其在深度学习网络中的应用。重点介绍了CAE的工作原理、关键数学公式以及在DeepLearning-toolbox中的实现细节,包括卷积、池化、反卷积操作及其对网络参数的更新策略。此外,文章还阐述了CAE在网络结构中的堆叠应用、实验结果及其在泛化性和鲁棒性方面的优势。
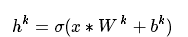
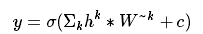
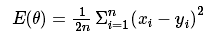
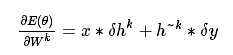
















 9606
9606

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








