【上采样】关于最近邻插值/双线性插值/反卷积这一篇就够了

在神经网络中，常常出现这样的情况：对某一特征表示进行不同程度的下采样得到各尺寸的特征图，而后分别应用 上采样，得到相同长宽的特征，而后进行级联操作，得到一个新的特征表示。比如下图所示就是一种使用反卷积进行上采样的实例：📖

接下来将依次详细的介绍以下三种常见的上采样方式，并附带Pytorch函数：

• 最近邻插值 Nearest Neighbor Interpolation 🌒
• 双线性插值 Bilinear Interpolation 🌓
• 反卷积 Transposed Convolution / Deconvolution 🌖

1 最近邻插值

最近邻插值是一种用于图像缩放和变换的简单插值方法。它的基本原理是，对于一个待插值的像素点（目标图像中的像素），我们找到在原始图像中距离该点最近的已知像素，并直接使用这个最近像素的值作为目标像素的值。😏

在Pytorch中，可用interpolate来实现，详情见interpolate。

import torch  
import torch.nn.functional as F  
input = torch.randn(1, 3, 64, 64) 
output = F.interpolate(input, size=(128, 128), mode='nearest') 

2 双线性插值

双线性插值是一种用于图像处理和数学插值的方法，常用于在二维空间中估算一个点的值。它适用于需要在已知的四个顶点值之间进行插值的情况，且不需要学习额外的参数。👍

双线性插值的基本思想是，在一个矩形区域内，利用该区域四个角点的值来估算该区域内任意一点的值。假设我们有四个已知点$Q$的值：

设待插值点的位置为 $P(x,y)$，其中$x$和$y$分别在已知点的横纵坐标范围内。我们可以按照以下步骤进行双线性插值：

$①$在$Q_{11}$和$Q_{21}$之间进行$x$方向的线性插值：
$$R_1=Q_{11}\cdot \frac{x_2-x}{x_2-x_1}+Q_{21}\cdot \frac{x-x_1}{x_2-x_1}$$
$②$在 $Q_{12}$ 和$Q_{22}$之间进行$x$方向的线性插值：
$$R_2=Q_{12}\cdot \frac{x_2-x}{x_2-x_1}+Q_{22}\cdot \frac{x-x_1}{x_2-x_1}$$
$③$在得到的$R_1$和$R_2$之间进行$y$方向的线性插值：
$$P=R_1\cdot \frac{y_2-y}{y_2-y_1}+R_2\cdot \frac{y-y_1}{y_2-y_1}$$

在Pytorch中，可用interpolate来实现，详情见interpolate。

import torch  
import torch.nn.functional as F  
input = torch.randn(1, 3, 64, 64) 
output = F.interpolate(input, size=(128, 128), mode='bilinear') 

3 反卷积

✈️以下将从卷积的基础概念出发，逐步探究反卷积的元素关系和尺寸关系。

3.1 卷积的基本概念

要弄清楚反卷积，首先必须得清楚卷积的概念，这里将常见的有关卷积形状的参数(不考虑通道数)列出如下：

参数名	参数简写
input_size	$i$
output_size	$o$
kernel_size	$k$
stride	$s$
padding	$p$
dilation	$d$

其中，dilation(译: 膨胀)控制卷积核采样元素之间的间距，如下图所示：

$d=1$	$d=2$

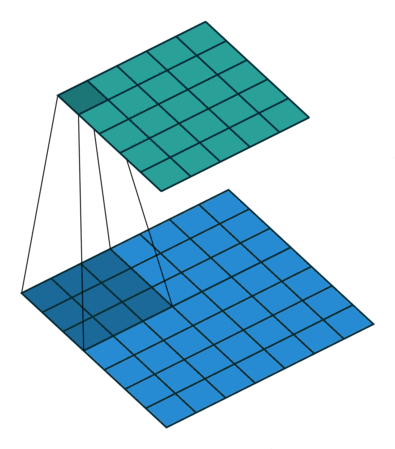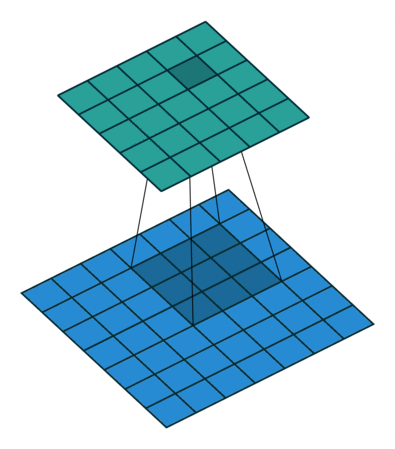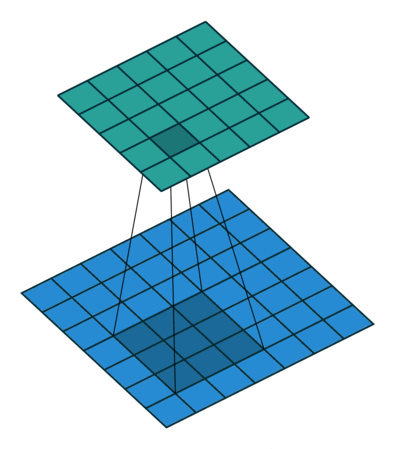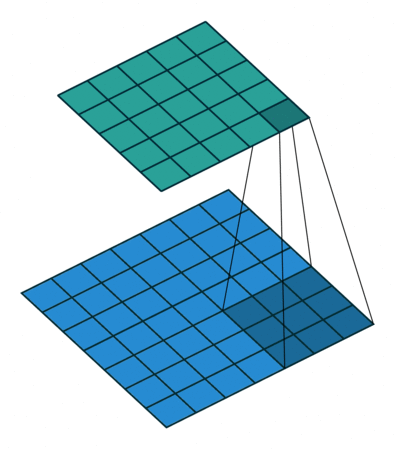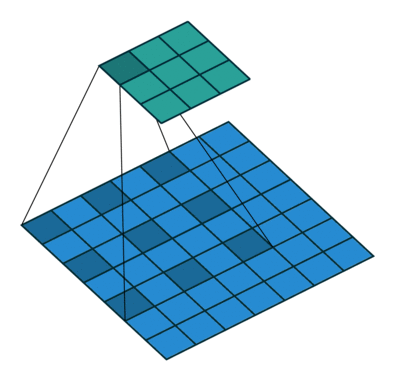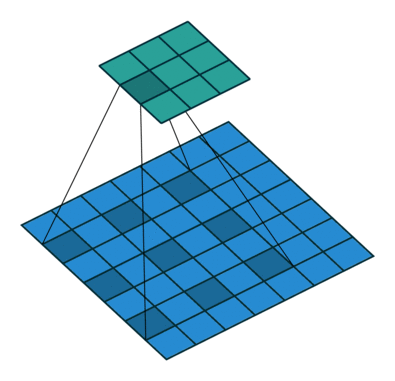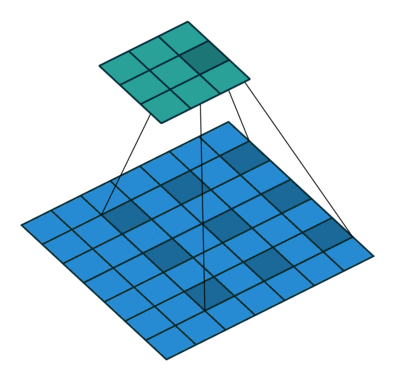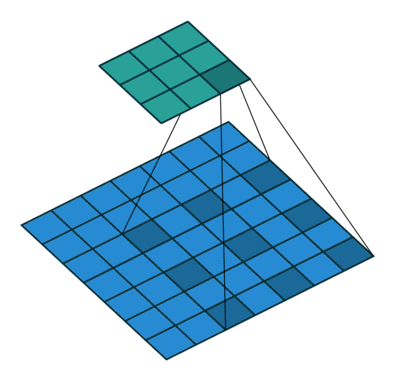3.2 反卷积的元素关系

⭐️首先明确反卷积并不是卷积的逆过程，更加准确的，应该称之为转置卷积。

反卷积是一种特殊的正向卷积，先按照一定的比例通过补 0 来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

接下来，通过一个例子来说明反卷积的定义：

假设有输入参数$i=4,k=3,s=1,p=0,d=1$，则有输出参数$o=2$：
$$K_{3\times 3}\ast X_{4\times 4}=Y_{2\times 2}$$
如果将输入输出矩阵展平为向量，将卷积核用稀疏矩阵表示，用矩阵乘法来表示上述卷积过程，则有：
$$K_{4\times 16}\times X_{16\times 1}=Y_{4\times 1}$$
因而当需要维持形状的不变性时，反卷积可表示为：
$$X_{16\times 1}=(K_{4\times 16}{)}^T\times Y_{4\times 1}$$
💫注意这里采用这种方式表示的反卷积并非卷积的逆过程，而只是为了维持形状不变性而采用的操作。实际中，由于反卷积的权重也是可以学习的，用反卷积对特征进行上采样依旧有效，所以我们只需保持形状不变性即可。

3.3 反卷积的尺寸关系

当简单考虑时，卷积操作有以下简单的尺度变换关系：
$$o=\frac{i+2p-k}{s}+1$$
而综合考虑时地，考虑到除不尽等因素，卷积操作有以下尺度变换关系：
$$o=\lfloor \frac{i+2p-[d(k-1)+1]}{s}\rfloor +1$$
如果不采用向下取整的符号，此关系又可写作：
{ o = i + 2 p − [ d ( k − 1 ) + 1 ] − a s + 1 a = { i + 2 p − [ d ( k − 1 ) + 1 ] } % s \begin{cases} o=\frac{i+2p-[d(k-1)+1]-a}{s}+1\\a=\{i+2p-[d(k-1)+1]\}\%s \end{cases} {o=si+2p−[d(k−1)+1]−a​+1a={i+2p−[d(k−1)+1]}%s​
而对于反卷积操作，我们根据上式，进行等价变换，将$i$用$o$表示，结果如下：
{ i = ( o − 1 ) s − 2 p + [ d ( k − 1 ) + 1 ] + a a = { i + 2 p − [ d ( k − 1 ) + 1 ] } % s \begin{cases} i=(o-1)s-2p+[d(k-1)+1]+a\\a=\{i+2p-[d(k-1)+1]\}\%s \end{cases} {i=(o−1)s−2p+[d(k−1)+1]+aa={i+2p−[d(k−1)+1]}%s​
接着我们用$i$表示反卷积的输入，$o$表示反卷积的输出，结果如下：
{ o = ( i − 1 ) s − 2 p + [ d ( k − 1 ) + 1 ] + a a = { o + 2 p − [ d ( k − 1 ) + 1 ] } % s \begin{cases} o=(i-1)s-2p+[d(k-1)+1]+a\\a=\{o+2p-[d(k-1)+1]\}\%s \end{cases} {o=(i−1)s−2p+[d(k−1)+1]+aa={o+2p−[d(k−1)+1]}%s​
上式便是反卷积尺寸上的数学表达式。😎

看到这个表达式是不是有点疑惑，求反卷积时，这个$a$怎么来呢？

在Pytorch中，卷积操作为ConvTranspose2d，详情见ConvTranspose2d。这个操作中默认$a=0$，但可以在合理设定$a$参数的情况下，指定输出的尺寸(有限制，不能随便指定)：

import torch
import torch.nn as nn
input = torch.randn(1, 16, 12, 12)
downsample = nn.Conv2d(16, 16, 3, stride=2, padding=1) 
upsample = nn.ConvTranspose2d(16, 16, 3, stride=2, padding=1)
#对此输入张量和卷积，会出现除不尽的情况，a≠0
output_down = downsample(input) #(1,16,6,6) 
output_up = upsample(ouput_down) #default: (1,16,11,11) 
output_up = upsample(ouput_down, output_size=input.size()) #(1,16,12,12)