分层卡方检验 & 卡方拟合优度案例教程

最新推荐文章于 2025-02-17 22:21:51 发布

spssau

最新推荐文章于 2025-02-17 22:21:51 发布

阅读量1.4k

点赞数 16

文章标签： SPSSAU spss 数据分析卡方检验

本文链接：https://blog.csdn.net/m0_37228052/article/details/143308736

版权

一、分层卡方检验

卡方检验研究的是分类变量X对分类变量Y的关系，这样的关系可能受到第三个混杂因素的影响。比如研究是否吸烟(X)与是否患某病(Y)的关系，专业上认为年龄起到干扰作用，将其纳入分析范畴作为分层项，这种分析称之为分层卡方检验。

1. 基本概念

当给交叉表卡方检验加入分层变量后，卡方检验被拆分到不同的层次水平，每一层均可单独完成交叉表卡方检验进行分析。但是研究者关注的是扣除分层因素的干扰影响后，列联表中行变量对列变量的影响是否显著。分层卡方可以用Cochran-Mantel-Haenszel检验(简称CMH检验)进行分析，可很好的解决“辛普森悖论”问题，常用于病例对照试验研究。

OR值是分层卡方中的一个重要概念。OR值(odds ratio)又称比值比、优势比，主要指病例组中暴露人数与非暴露人数的比值除以对照组中暴露人数与非暴露人数的比值，是流行病学研究中的一个常用指标，反映的是疾病和暴露的关联强度。例如在研究高血压对心肌梗死的影响时，OR值为3.5，其通俗理解即患高血压的人发生心梗的风险是未患高血压的3.5倍。在本书《SPSSAU科研数据分析方法与应用》后续的Logistic回归、医学研究内容中还会详细介绍其应用。

目前应用较多的是2×2×K结构数据资料的分层卡方检验(即X和Y均为2分类，分层项为K层)。该方法一般只能考察或控制一个混杂因素，当混杂因素超过1个时，可考虑Logistic回归分析。

2. CMH分析思路

Cochran-Mantel-Haenszel分层卡方检验的基本思想是对各层的OR值进行合并，并进行合并后后的独立性卡方检验，其分析思路见图 4-17。

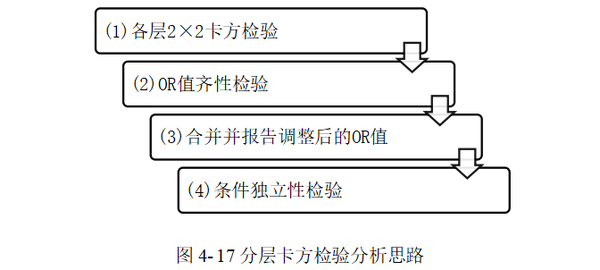
(1) 各层2×2卡方检验p值、OR值

分别就各层频数数据进行普通的2×2四格表卡方检验，解释和分析各层中行变量与列变量间的关系，计算并报告OR值。

(2) OR值齐性检验

对各层OR值进行齐性检验，如果各层OR值同质或一致，说明当前纳入的分层因素没有混杂干扰作用或干扰很弱，各层的OR可进行合并，相当于消除分层因素影响后用一个统一的OR值评价行与列变量的影响关系；如果各层的OR值不同质或不一致，则说明分层因素存在混杂干扰作用，此时应分别报告各层的OR值。

一般用Breslow-Day检验和Tarone´s检验完成OR值齐性检验，当p值小于0.05时，说明分层的OR值是不一致的；当p值大于0.05时则说明各层OR值是一致的。

(3) 合并并报告调整后的OR值

当上一步检验出OR值具有一致性时，提示可对各层OR值进行合并计算，合并后得到一个调整后的OR值，它的大小反映的是排除分层因素影响后，行变量对列变量的影响程度。在病例对照研究中，即排除分层因素影响后，暴露因素对结局的影响。

(4) 条件独立性检验

排除分层因素干扰，相当于是控制了分层因素后影响行变量与列变量的独立性或差异性关系，也就是分层卡方检验的结果或结论。

3. 实例分析

接下来结合具体案例进一步介绍分层卡方检验在科研中的应用。

【例4-14】某研究调查了口服避孕药(OC)与心肌梗死的情况，考虑到年龄是一个可能的混杂因素，将其纳入调查，获得的数据见表 442，试分析在年龄的影响下心肌梗死与是否服用避孕药有无关系。数据来源于张文彤(2002)，数据文档见“例4-14.xls”。

（1）数据与案例分析

定类数据编码情况，分组变量“避孕药”：数字1代表不服用OC，数字2代表服用OC；结局变量“心肌梗死”：数字1代表对照组，数字2代表病例组；分层项变量“年龄”：数字1代表﹤40岁，数字2代表≥40岁。

考察两个分类变量间的关系，显然卡方检验是可选方法之一。现在还需要考察第三个分类变量的干扰，可以将其作为分层项，执行分层卡方检验。

（2）分层卡方检验

读入数据后，在仪表盘中依次选择【实验/医学研究】→【分层卡方】模块，按图 418所示的操作设置。平台的【分层卡方】模块支持普通数据格式与加权数据格式两种，如果有加权项则“加权项”框中下拉选择具体的变量标题，如果没有加权项则不用选择。

最后单击【开始分析】，参照前面介绍的分析思路，按以下顺序对结果进行解释和分析。

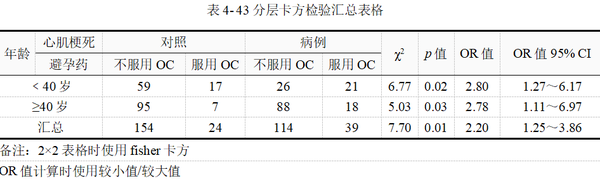
（3）各层2×2卡方检验

本例共有两层，由表 443可知，不论年龄﹤40岁还是≥40岁，心肌梗死与是否服用避孕药均有关联(卡方检验p值均﹤0.05)。年龄﹤40岁和≥40岁两层的OR值依次为2.80、2.78，均大于1，提示不论年龄﹤40岁还是≥40岁，服用避孕药是心肌梗死的危险因素。

（4）OR值齐性检验

在研究结果中包括各层OR值还是合并OR值，其前提条件是各层OR值是否满足齐性(同质或一致)。Breslow-Day-Tarone检验结果见表 4-44。

本例p值为0.99﹥0.05，表明两个年龄层间OR值同质或具有一致性。因此接下来我们需要解读合并的OR值以及条件独立性检验结果。如果OR值异质，则返回上一个步骤分别报告各层的OR值。

（5）合并并报告调整后的OR值

在表 445中同时给出了合并计算的OR值，以及分层卡方检验结果(条件独立性检验)。

合并OR值(Mantel-Haenszel Common)，即扣除分层变量影响后分类变量X对分类变量Y的调整后OR值。在本例中即排除年龄混杂影响后，是否服用避孕药对心肌梗死的优势比。本例调整后OR值=2.79，95% CI为[1.53,5.08]，置信区间不包括1，结论是扣除年龄干扰影响后，服用避孕药患心肌梗死的危险度是未服用的2.79倍。

（6）条件独立性检验(分层卡方检验)

分层卡方检验的卡方值=10.73，p值﹤0.05，表明扣除年龄干扰影响后，心肌梗死与服用避孕药相关。

本例最终的结论：综合认为，扣除年龄干扰影响后，心肌梗死与服用避孕药相关(p﹤0.05)，服用避孕药患心肌梗死的危险度是未服用的2.79倍。

二、拟合优度检验

拟合优度检验(Goodness of fit test)，用于判断实际观察的类别频数分布比例与已知类别频数分布比例是否符合的分析方法。

原假设样本实际频数分布与理论频数分布一致或相同，备择假设则为不一致或不相同，构造并计算卡方统计量，并计算概率p值，利用p值进行统计推断。当p值小于0.05时拒绝原假设，认为实际频数分布与理论频数分布不相符；反之当p值大于0.05时认为频数分布一致。

常见的包括等比例假设与不等比例(指定比例)假设，等比例假设比如某高校研究生招生，男研究生100名、女研究生120名，分析研究生性别比例有无差别(默认假设男女比例相同)；不等比例假设比如某高校研究生招生，原计划男女性别比例为7:3，实际招男研究生50名，女研究生35名，分析实际研究生性别比例是否与原计划相符。

【例4-15】某高校研究生招生，原计划招生的男女性别比例为7:3，实际招男研究生50名，女研究生35名，分析实际研究生性别比例是否与原计划相符。