二元logistic回归分析原理及案例教程

二元Logistic回归中因变量只有两种结局，且两个结局是互斥的。举个例子进行说明，现在假设y=1为死亡，y=0为未死亡，Logistic回归最终可以做到的是病例判定为死亡或未死亡，以及出现该结局的概率。死亡的概率为P，则未死亡的概率为1-P，令ln(P/1-P)=logit(P)，这一过程称为logit对数变换。

1. 二元Logistic回归模型

当有多个因素时，Logistic回归的一般形式为：

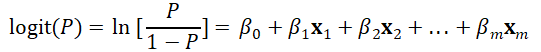
整个模型以最大似然法进行参数估计，以医学、流行病学为例，模型中有以下主要概念：

(1) P/1-P：称为比值或优势(odds)，ln(P/1-P)=logit(P)称为优势的对数，大量实践证明logit(P)与定量自变量呈线性关系。

(2) OR值(odds ratio)：又称比值比、优势比，主要指病例组中的比值P/1-P除以对照组中的比值P/1-P，是流行病学、医学研究中的一个常用指标。

(3) 偏回归系数βj (j=1,2,…,m)：表示在其他条件不变情况下，自变量每改变一个单位时Logit(P)的改变量。回归系数如果是正数，表示自变量与因变量正相关；如果是负数则表示自变量与因变量负相关。

(4) 回归系数与OR值的关系：回归系数主要解读自变量的显著性以及对因变量影响的正负方向，OR值用于衡量自变量对因变量作用程度，OR值等于回归系数的自然对数值。例如自变量X的偏回归系数为0.6，则其

回归系数、OR 值及对因变量的意义如表 5-19 所示：

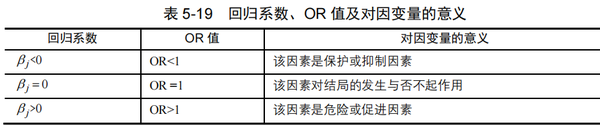
• 若 β j 等于 0，则 OR 值等于 1，表示该因素对结局的发生与否不起作用。
• 若 β j 为正数，则 OR 值大于 1，表示该因素是危险或促进因素。
• 若 β j 为负数，则 OR 值小于 1，表示该因素是保护或抑制因素。

2. 逐步法筛选自变量

和线性回归类似，多因素Logistic回归时也可以采用逐步回归的方式对变量进行筛选，比如向前逐步、向后逐步或逐步法，尤其是逐步法在多因素Logistic回归受到科研工作青睐。此处注意，SPSSAU采用Wald检验进行自变量的逐步筛选。

3. 二元Logistic回归实例分析

【例5-8】现收集到银行贷款客户的个人负债信息，以及曾经是否有过还贷违约的记录，数据中各变量赋值说明如表 5-20所示，试分析是否违约的相关因素。数据来源于SPSS统计软件自带数据集“bankloan.sav”，数据文档为“例5-8.xls”。

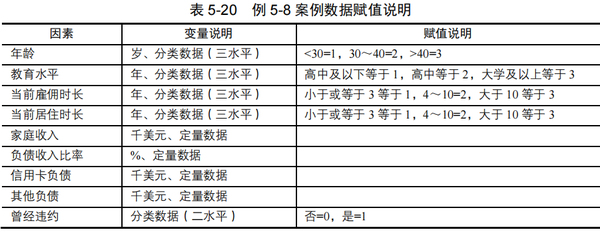
1) 基本条件判断

研究贷款违约发生的相关因素，因变量“曾经违约”有两种结局，因此选择使用二元Logistic回归。通过【通用方法】→【频率】模块，针对“曾经违约”进行频率统计，曾经发生过违约行为的有183例，按样本量与自变量个数10倍关系计算，样本量基本满足本次分析需要。

通过【通用方法】→【线性回归】模块，以“曾经违约”为因变量，其他数据为自变量进行线性回归，在输出的结果中发现，各自变量的VIF均未超过5，初步认为自变量间不存在共线性问题。

2) 建立Logistic回归模型

本例要考察的自变量有8个，在建立多因素回归模型之前，可先通过卡方检验、t检验分析了解各自变量对因变量的影响。

（1）单因素分析

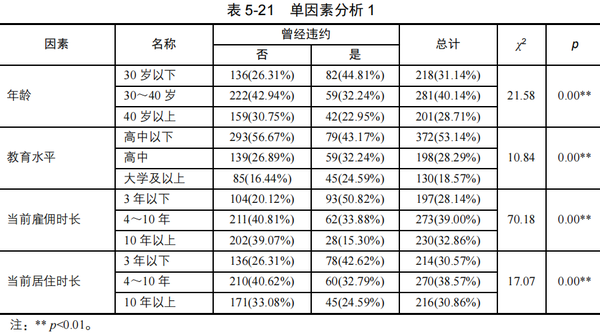
本例通过【实验/医学研究】→【卡方检验】模块，分析“年龄”、“教育水平”、“当前雇佣时长”、“当前居住时长”与“曾经违约”间的关系，结果见表5-21。

通过【通用方法】→【t检验】模块，分析“家庭收入”、“负债收入比率”、“信用卡负债”、“其他负债”与“曾经违约”间的关系，结果见表5-22。

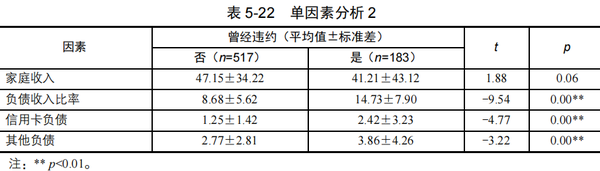
单因素分析时，假设检验的显著性水平一般可以适当放宽到0.1甚至0.2。由表5-21～表5-22可知，经卡方检验与t检验，按α=0.1的显著性水平，所有自变量的p值均小于0.1，说明待分析的8个自变量分别和因变量“曾经违约”均有相关性。

单因素阶段有显著性的各自变量继续进行多因素二元Logistic回归分析，因素较多时可采用逐步回归进行筛选。SPSSAU基于Wald检验提供三种逐步回归方法，分别是逐步法、向前法、向后法，逐步法是向前与向后法的综合应用，一般情况下使用逐步法居多。

（2）建立多因素Logistic回归模型

本例变量“年龄”、“教育水平”“当前雇佣时长”、“当前居住时长”为多分类变量，通过【数据处理】→【生成变量】模块先对这四个变量进行哑变量转换。

依次选择【进阶方法】→【二元Logit】模块，“曾经违约”拖拽至【Y(定类)】框内，特别注意，因变量的两个水平数字编码必须是0和1，可提前通过【数据处理】→【数据编码】模块查看或进行编辑转换。将“家庭收入”、“负债收入比率”、“信用卡负债”、“其他负债”以及“年龄”、“教育水平”、“当前雇佣时长”、“当前居住时长”这四个变量生成的哑变量全部拖拽至【X(定量/定类)】框内，注意本例全部选择第一个水平作为参照，四个分类变量的1水平哑变量不移入【X(定量/定类)】框。勾选【保存残差和预测值】，具体操作界面见图 5-25，最后单击【开始分析】。

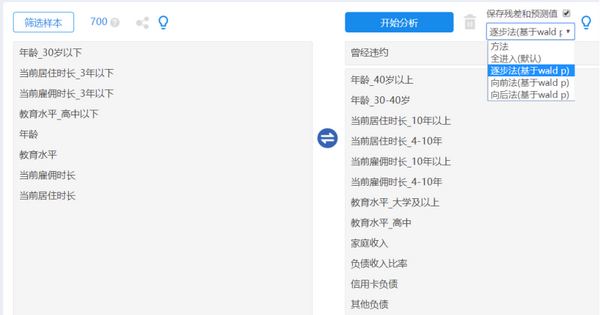
Logistic回归输出包括基本汇总、模型似然比检验、分析结果汇总、回归预测准确率、Hosmer-Lemeshow拟合度检验、coefPlot图等结果，我们可以按步骤进行解读和分析。

（3） Logistic回归模型的检验与评价

模型似然比卡方检验用于对整体模型有效性进行分析，本例结果见表5-23，卡方值=229.287，p﹤0.01，认为二元Logistic回归模型总体上有统计学意义，模型中引入的自变量至少有一个对因变量有影响，模型是有效的。

赤池信息准则AIC、贝叶斯信息准则BIC，这两个统计量用于模型间的比较，取值均是越低则模型拟合越好，本例只有一个有效模型，没有可比较的对象，因此此处AIC和BIC并无实际用处。“-2对数似然值”即其他统计软件工具输出的“-2LL”统计量，也用于多个模型间的比较，取值越低则模型拟合越好。

Hosmer-Lemeshow拟合度检验结果见表5-24，卡方值=5.219，p=0.734﹥0.05，说明模型拟合良好。

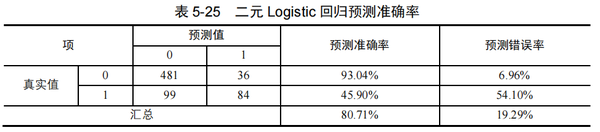
如上表5-25所示，本例二元Logistic回归模型对结局0即未违约的预测准确率为93.04%(481/517)，对结局1即违约的预测准确率为45.90%，总体预测准确率80.71%。从银行贷款业务风险预警的角度，本例更关注对违约结局的预测能力，显然45.9%是比较低的，该模型的实用价值有待进一步提高。

注意，有些研究并不看中模型的预测能力，而主要关注的是因变量的相关影响因素。因此预测准确率表的结果应综合研究目的来解读。

在模型分析结果汇总表(偏回归系数解释时使用)，即表5-26的底部，SPSSAU提供了三个伪R方指标，其含义类似于线性回归中的决定系数R方，其取值越大越好，在实际分析中应用较少，可以不做关注。

（4）偏回归系数与OR值解释与分析

本次Logistic回归各因素自变量偏回归系数检验及OR值结果，见表5-26。

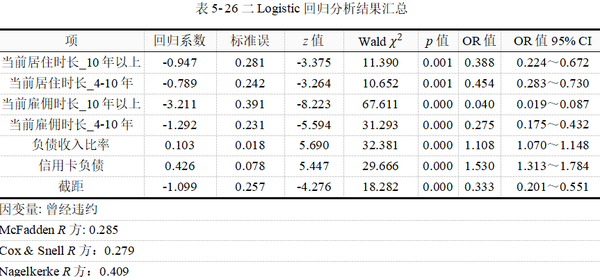
通过逐步法，模型自动根据显著性情况对自变量进行引入或剔除。4个定量数据中，“负债收入比率”、“信用卡负债”Wald卡方检验显示，p值均小于0.05，它们对“曾经违约”的影响有统计学意义。

“当前居住时长”、“当前雇佣时长”的4个哑变量，Wald卡方检验显示，p值均小于0.05，它们对“曾经违约”的影响也有统计学意义。其他没有引入模型的，比如“家庭收入”、“其他负债”、“教育水平”的2个哑变量，“年龄”的2个哑变量均没有统计学意义。

标准误和z值这两个为中间计算过程的统计量，标准误不宜过大，z值一般不用解读。表中重点是各因素的偏回归系数、OR值及其95%置信区间。

2个定量数据“负债收入比率”、“信用卡负债”的偏回归系数为正数，认为其与“是否违约”存在正向相关关系，相对应的OR值大于1，OR值95% CI不包括1。说明信用卡负债、负债收入比率越高越容易出现偿还贷款违约的情况。以“信用卡负债”为例，Wald 卡方值=29.666，p﹤0.01，认为其对“是否违约”的影响有统计学意义，二者存在正相关关系。OR值=1.53﹥1，说明其为发生违约的危险因素或促进因素，信用卡负债每增加一个单位，其发生违约的可能性是原来的1.53倍，或发生违约的可能性比原来增加53%。

4个哑变量的偏回归系数均为负数，说明其与“曾经违约”存在负相关关系，相对应的是OR值均小于1，OR值95% CI不包括1。说明当前居住地居住时长4年以上、10年以上，当前雇主工作时长4年以上、10年以上对“是否违约”起到抑制作用，居住时长、工作时长越长(稳定)则越不容易出现还贷违约的情况。以“当前雇佣时长_10年以上”为例，Wald 卡方值=67.611，p﹤0.01，相较于“当前雇佣时长_3年以下”认为其对“是否违约”的影响有统计学意义，二者存在正相关关系。OR值=0.04﹤1，说明其为发生违约的保护因素或抑制因素，当前居住地居住时长每改变一个等级，其发生违约的可能性是原来的0.04倍，或发生违约的可能性比原来降低99.6%。

（5） 结果报告

本例建立的贷款违约二元Logistic回归模型为：

ln(P/1-P)=-1.099 - 0.947×当前居住时长_10年以上 - 0.789×当前居住时长_4-10年 - 3.211×当前雇佣时长_10年以上 - 1.292×当前雇佣时长_4-10年 + 0.103×负债收入比率 + 0.426×信用卡负债

其中P代表曾经违约为1的概率，1-P代表曾经违约为0的概率。总体而言模型有统计学意义。“负债收入比率”和“信用卡负债”正向影响违约的发生，而“当前居住时长”和“当前雇佣时长”则反向抑制违约的发生。这些对违约有显著影响的因素作用，见图 5-26。

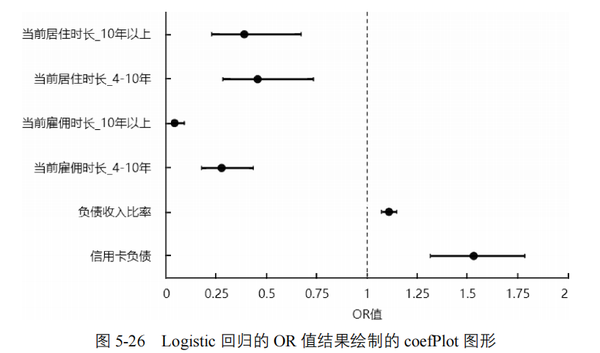
coefPlot图形非常直观地展示了模型中引入的自变量，以及各自变量对因变量影响的OR值情况。图中垂直的虚线代表OR=0，为无效线，图中的横线段为各自变量的OR置信区间，线段中间的圆点为具体的OR值。各自变量的OR值置信区间和虚线无交叉或重叠，则表示对应的自变量有显著性，位于虚线右侧表示OR值大于1，危险因素；位于虚线左侧表示OR值小于1，为保护因素。

---

以上内容摘自《SPSSAU科研数据分析方法与应用》第5章——相关影响关系研究，书中不仅涵盖了数据清理、统计分析和模型构建等内容，还提供了丰富的案例，以便于读者在实际研究中应用。