目录
1.变量的独立性
例:
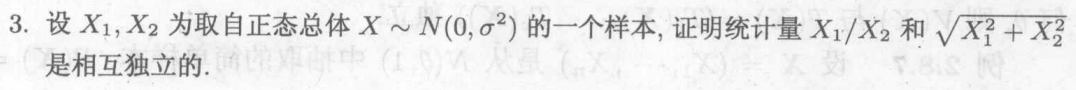


即为u的概率密度函数可以单独分离出来,得到的结果与无关,v的概率密度函数可以写成指数族的自然形式
2.正交变换
https://www.zhihu.com/question/401373076![]() https://www.zhihu.com/question/401373076
https://www.zhihu.com/question/401373076
正交变换不改变原向量的长度,向量之间的内积,向量之间的夹角
将原来的图像不规则的表达式用规则的表达式表达出来,本质上换了一个坐标轴,但是图像仍然是不变的

引理:
若相互独立,
,当A为正交矩阵,Y=AX,记
,
,则
之间相互独立服从正态分布,
,
,b = Aa
独立的正态分布随机变量正交变换后仍然独立
原随机变量X~i.i.d标准正态分布,则变换后的Y~i.i.d标准正态分布。
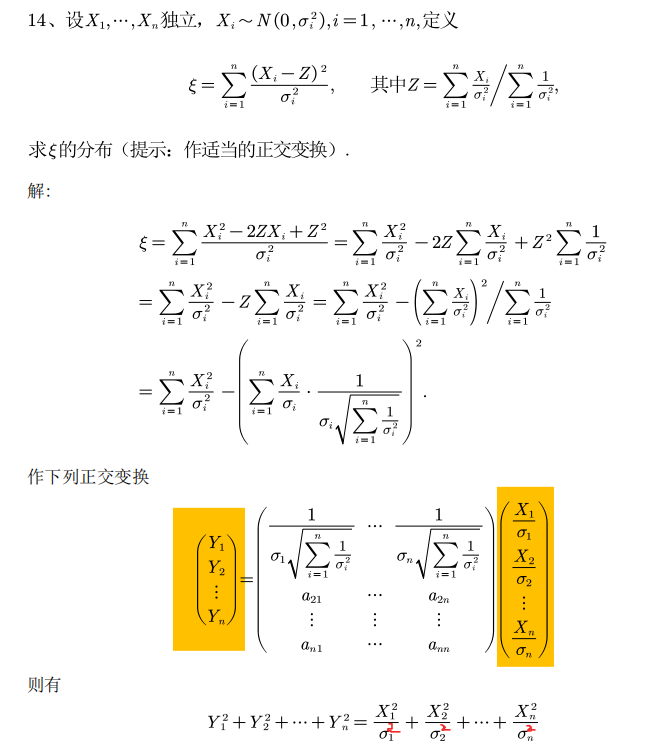
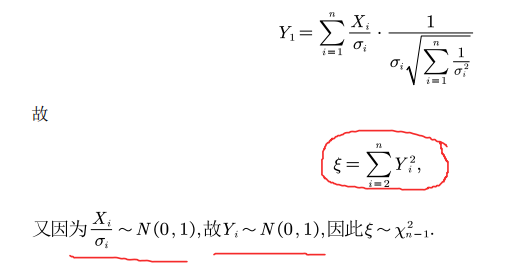
3.jacobi行列式与概率密度的关系
行列式的实质是进行变量变换后面积变化的比例,而求积分就是在求函数所围成的面积,所以函数进行变量变换后要乘以面积变化的比例,也就是这个雅可比行列式.


当然运用jacobi需要一些条件,如一维就是有反函数,严格单调函数必有反函数
4.伽马分布(Ga分布)
https://blog.csdn.net/qq_38406029/article/details/120225074![]() https://blog.csdn.net/qq_38406029/article/details/120225074https://blog.csdn.net/ma123rui/article/details/103056206
https://blog.csdn.net/qq_38406029/article/details/120225074https://blog.csdn.net/ma123rui/article/details/103056206![]() https://blog.csdn.net/ma123rui/article/details/103056206
https://blog.csdn.net/ma123rui/article/details/103056206
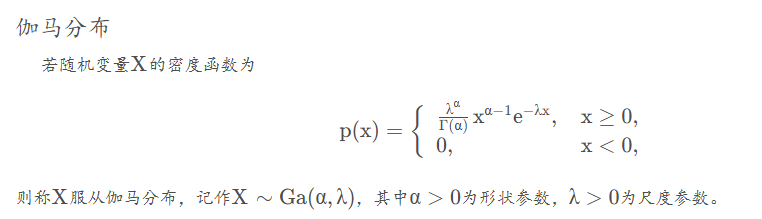

伽马分布的可加性:

两点分布,泊松分布,指数分布,正态分布,卡方分布均具有可加性
5.如何求一个函数的概率密度
a.利用特征函数和概率密度的唯一性来根据特征函数来确定概率密度函数,加法更加简单
b.利用jacobi行列式求变量之间的转换
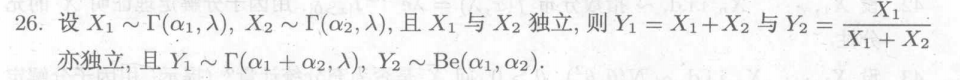

6.抽样分布
6.1抽样分布
统计量T = T(X1,X2,X3,...,Xn)的分布称为抽样分布
一个统计量的精确的分布函数形式一般是很难得到的
假设是在简单随机抽样的情况下,样本之间满足独立同分布
总体,
样本之间的联合分布
对于,如何去算他的分布?
对于概率论,我们学过的,求两个随机变量和的分布,如果两个分量独立,我们一般采用的是卷积的方法,但是卷积一般是比较麻烦的方法,根据时域和频域的变换关系,时域的卷积对应频域的乘法,乘法更加简单。
由此引入特征函数,即为傅里叶变换:
特征函数和分布函数是一一对应的,因此只要知道特征函数就能得到分布函数。
关于特征函数:
https://blog.csdn.net/wxc971231/article/details/121219832![]() https://blog.csdn.net/wxc971231/article/details/121219832e指数的一个作用就是可以将加法变成指数相乘
https://blog.csdn.net/wxc971231/article/details/121219832e指数的一个作用就是可以将加法变成指数相乘
例:总体满足(
-分布)
,
相关性质:,
,
,
求的分布/概率密度
I为示性函数,即在给定区间取值为1
推导总体的情况,用样本的特征函数和总体对照,来判断样本的概率密度函数
一般的分布,特征函数为
当=1时,
分布此时为指数分布
当总体服从指数分布时:
,
对比总体一般的特征函数:
故
关于伽马分布:
https://blog.csdn.net/qq_38406029/article/details/120225074![]() https://blog.csdn.net/qq_38406029/article/details/120225074https://blog.csdn.net/ma123rui/article/details/103056206
https://blog.csdn.net/qq_38406029/article/details/120225074https://blog.csdn.net/ma123rui/article/details/103056206![]() https://blog.csdn.net/ma123rui/article/details/103056206
https://blog.csdn.net/ma123rui/article/details/103056206

当时是指数分布,当
时是自由度为n的卡方分布
伽马分布的可加性:

两点分布,泊松分布,指数分布,正态分布,卡方分布均具有可加性
6.2 正态总体下的样本统计量的分布
对于正态总体,同理各个样本的线性组合可用特征函数求解:至少是独立的,同分布是后两种
代数形式表达:
设总体,在独立同分布的假设条件下,则联合分布为
那么如何求,
,
a.定理1,正态分布样本的线性组合
总体服从正态分布,样本的线性组合也服从正态分布
那么根据上面的方法,,计算和的特征函数与原函数的相对照,得到:
在该假设![]() 下,分布为(独立)
下,分布为(独立)
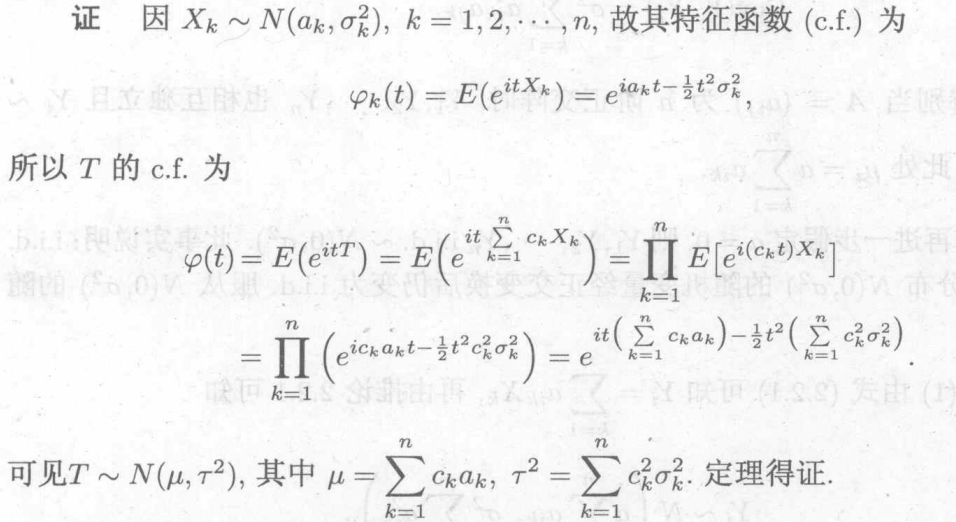
独立同分布情况下,
取,
当样本足够多时,依概率收敛于一个数,即为大数定律
用向量形式表达,即向量中的每一个分量都是一个随机变量,且分量之间相互独立,表达形式更加简洁:
,
,
,
,
一般,
,
,
,
,
此时为两个随机变量之间不是独立的:
对于,
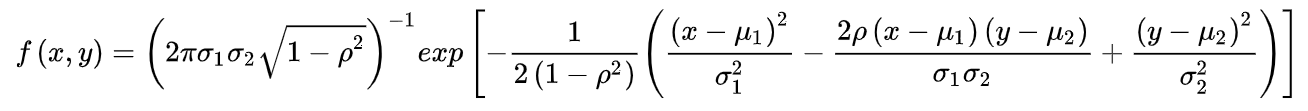
用向量如何表示?
记,
,
二阶矩阵的逆=行列式分之1乘以(主对角线对调,副对角线取负数)
,
由此求得:
再进一步还有n维:
,当随机变量之间独立,且
时:
因为独立所以此时协方差矩阵为单位阵
记,
,
特别的当Y = AX时,即,利用雅可比行列式和反函数,求得Y的分布:
Y = AX,则,
当A为正交矩阵即时:A的每一行每一列都是单位正交基
此时,
由此得到一个引理:
若相互独立,
,当A为正交矩阵时,Y=AX,记
,
,则
之间相互独立服从正态分布,
,
,b = Aa
证明:即求解Y的联合分布函数,将原来的X的联合概率密度函数处的X都换成,观察求得的概率密度函数,满足正态分布的形式,故可以得到结论
b.定理2,独立同分布的线性变换——>正交变换,即将1维升到n维
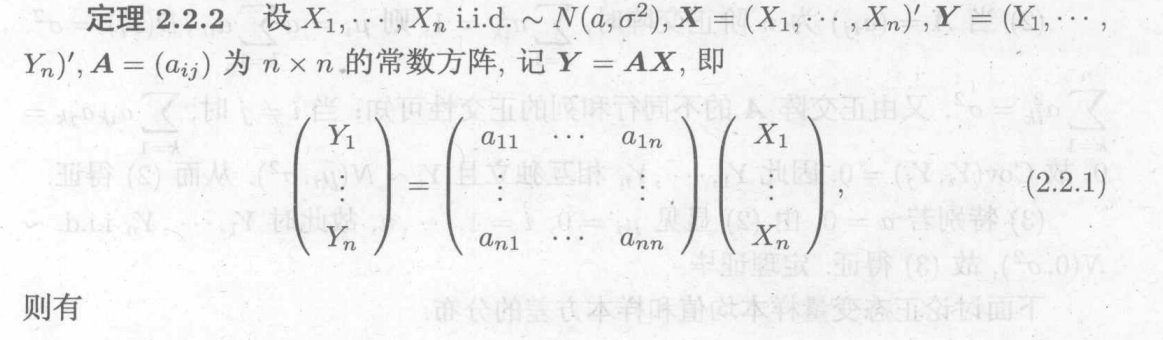
经过正交变换后原来独立的现在仍然独立,原来服从正态分布现在仍然服从正态分布


c.定理3(样本均值和样本方差的分布)

一般情况下的正态总体的n维随机变量的分布:
当独立同分布时:
,
,平方和,减去的均值相同
当独立不同分布时:
均值不同:
,
,
,平方和,减去的均值不同
方差不同:
,
,加权平方和
当不独立时:
此时不是一个对角矩阵,而是一个由相关系数,方差等组成的矩阵,
总结:
该式对任意情况下均成立

如何证明?(猜想)
利用此公式求解,即令
,此时的
利用,然后再求边缘概率密度函数即可求出
6.3 次序统计量的分布
目前还没有用到,用到再详细了解
单个次序统计量的分布:

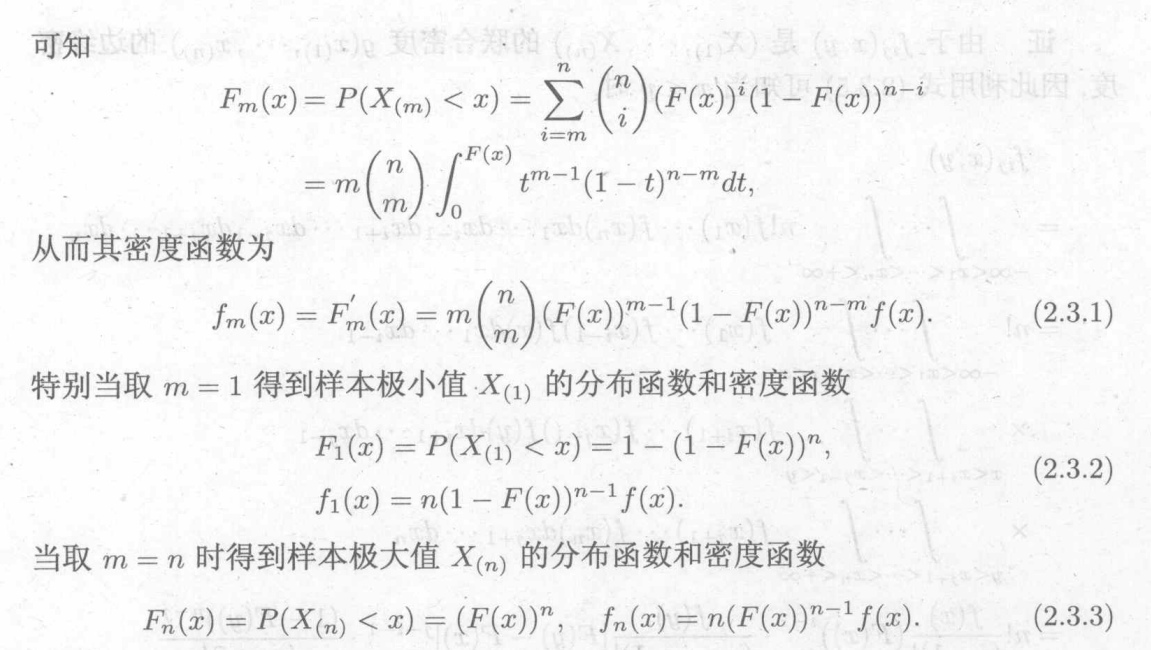
任意两个次序统计量的分布:
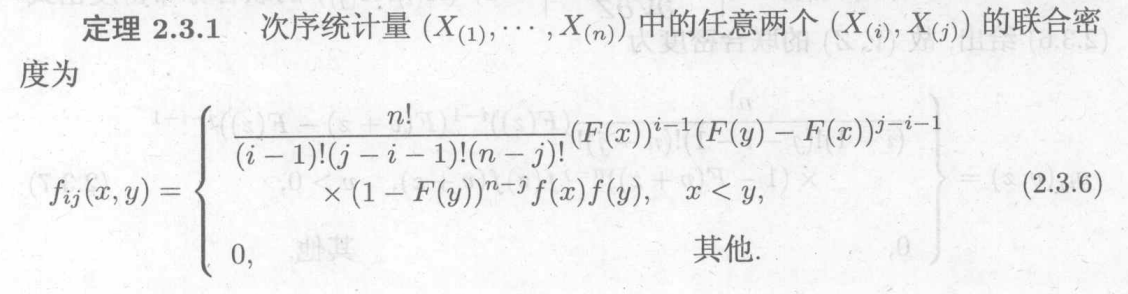
n个次序统计量的分布:
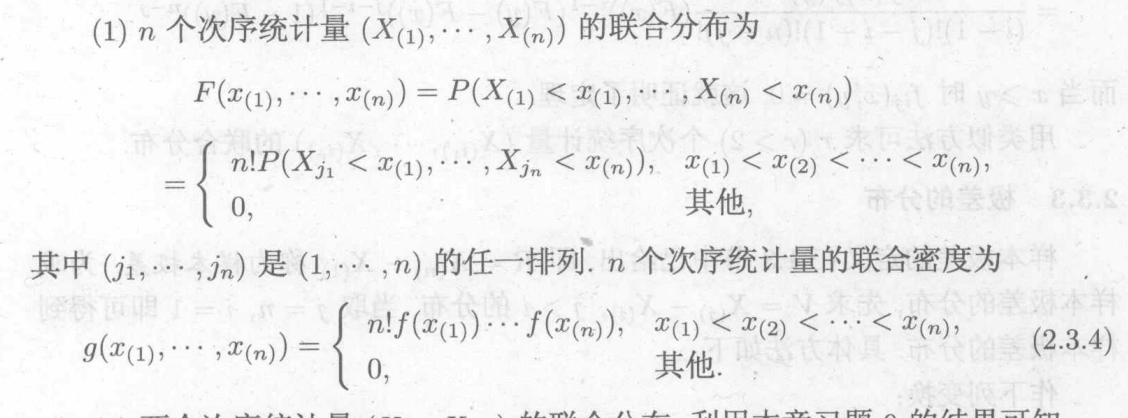
极差的分布:
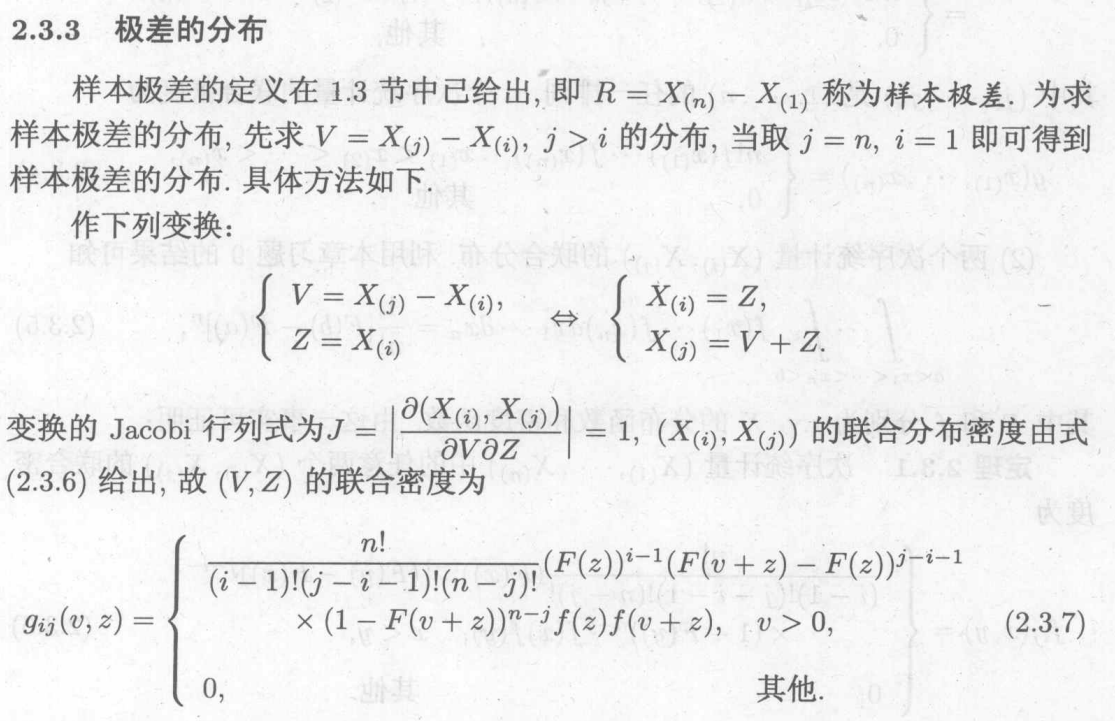
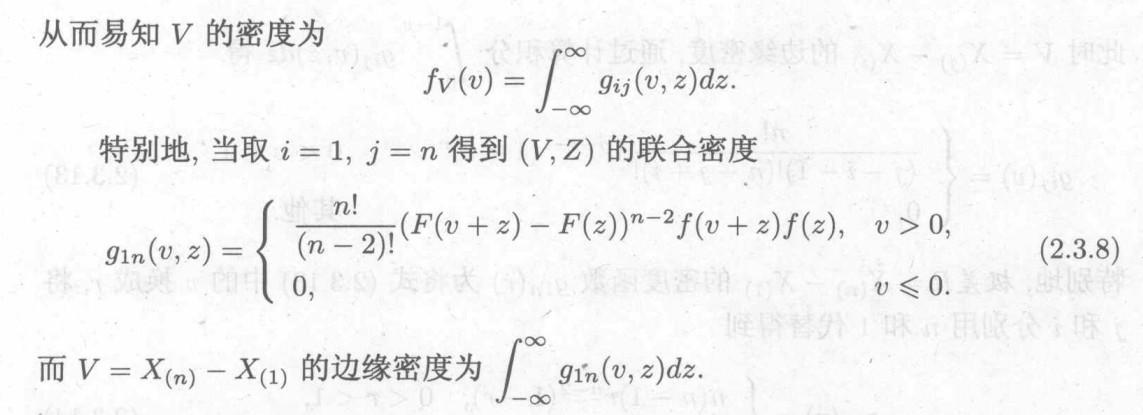
当每个随机变量服从均匀分布时:(即将均匀分布的函数代入上式)


6.4 三大常用统计分布
a.分布:
n个i.i.d的标准正态分布之和
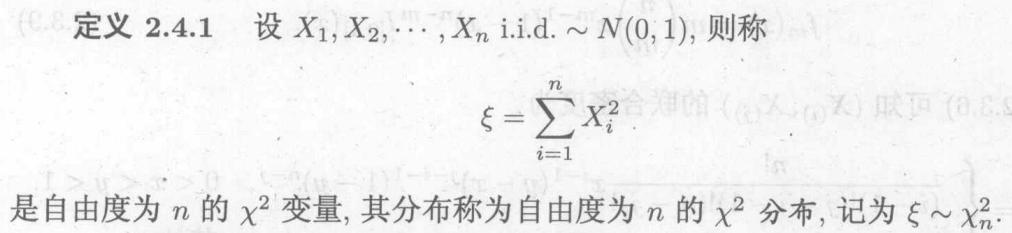

如何推导其概率密度函数?即为n元的积分,利用球坐标变换
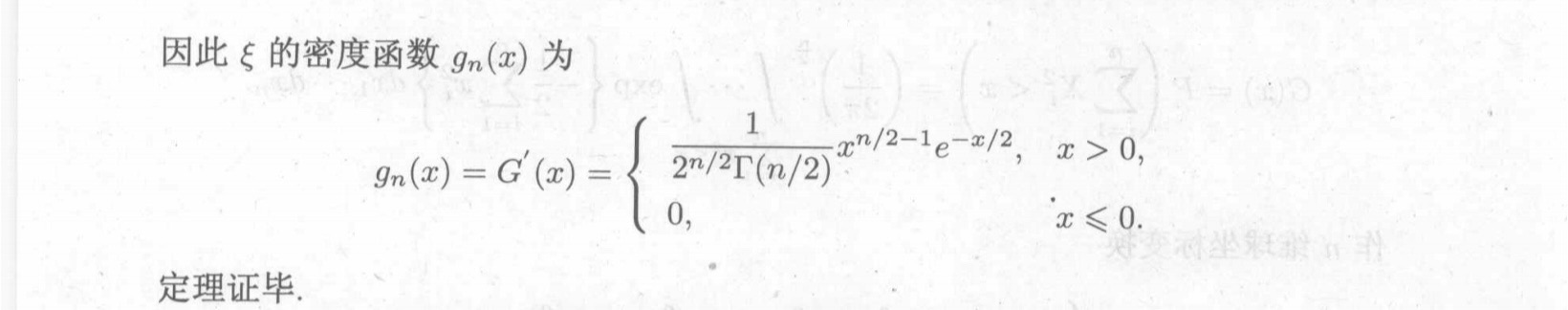
当n足够大时,趋向于非中心的正态分布
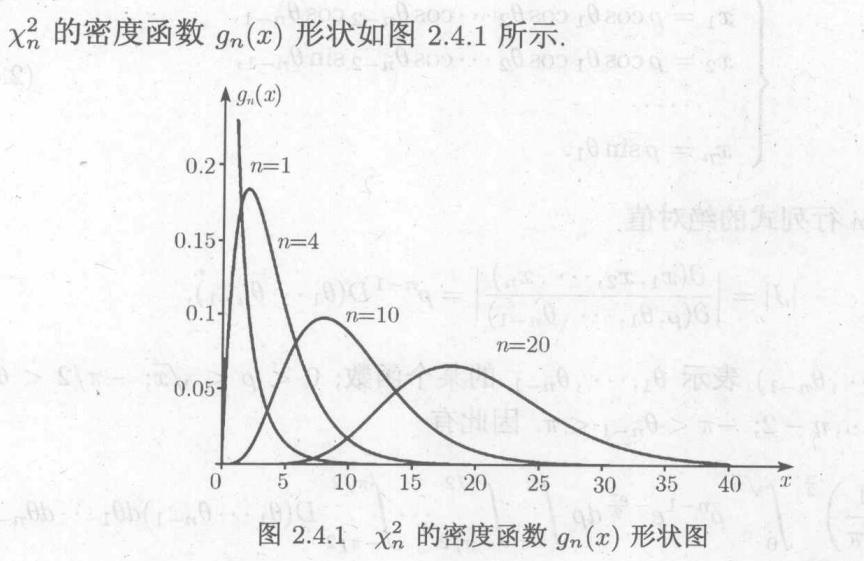

上分位数:
,则称c为上
分位数,与此对应
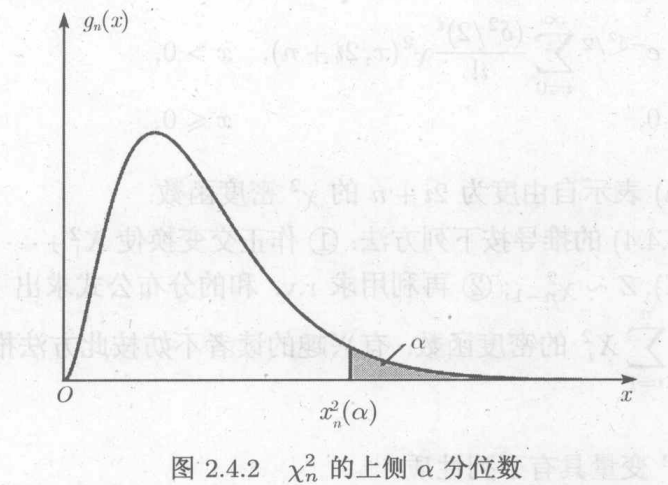
性质:

对于均值和方差,可以利用独立的性质,将n个变为1个,再利用期望和方差的公式,同时利用标准正态分布奇次项和偶次项的期望的性质。
对于求和,可以认为是增加了标准正态分布变量的数目。
非中心分布:
定义:


如何推导?

性质:

b.t分布
即为一个标准正态和一个分布之和,t分布的平方服从F(1,n)
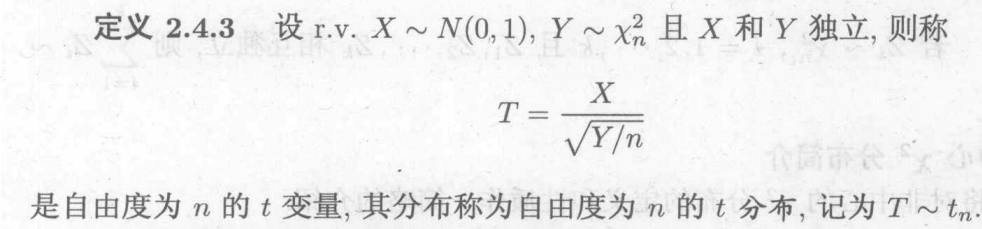
利用求商的概率密度函数,先求出的分布函数,再求T

当n足够大时,t分布趋向服从标准正态分布

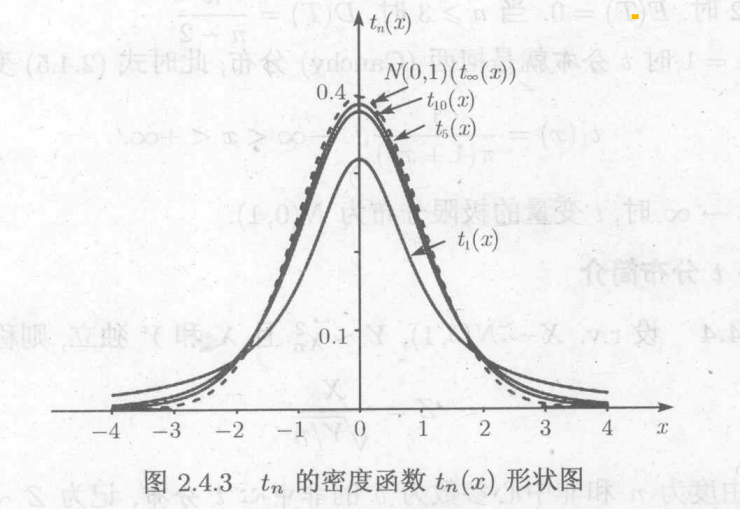
上分位数:
,则称c为上
分位数,与此对应
,当
时(n取30),
,即为标准正态上
分位数
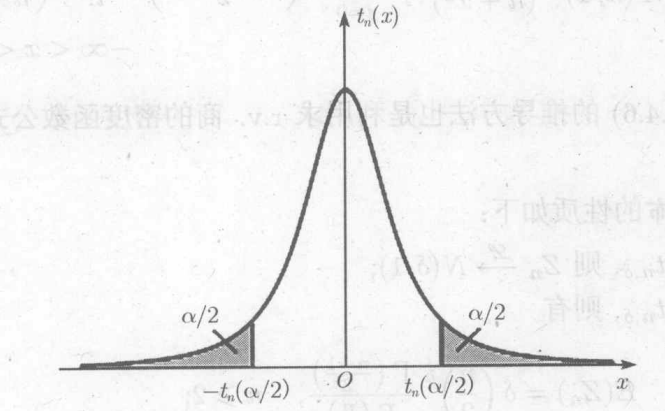
性质:

非中心t分布:
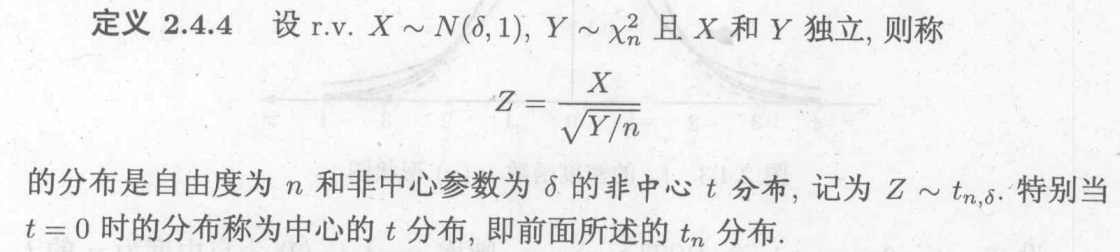

c.F分布
两个分布的商

利用商的概率密度
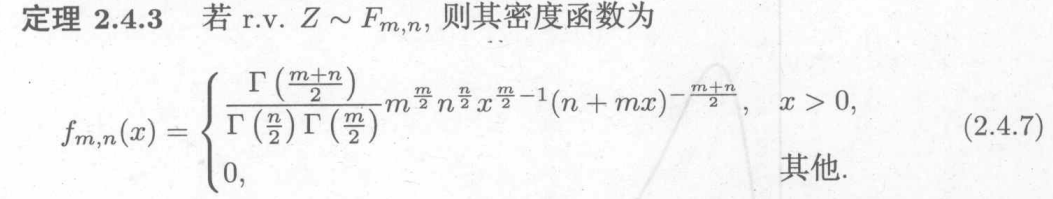

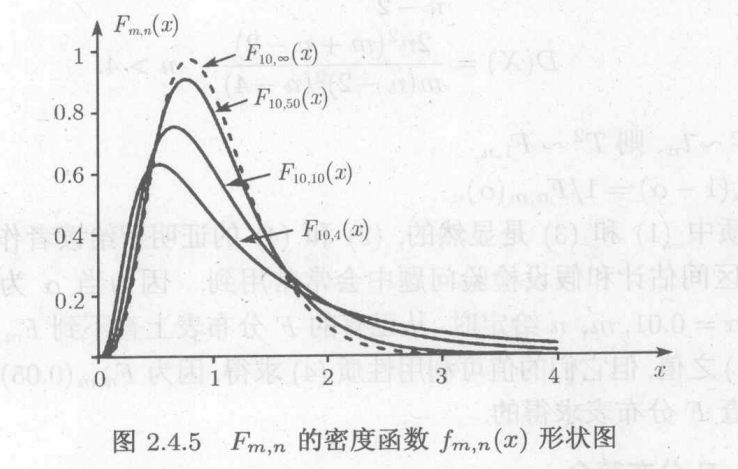
上分位数:
,则称c为上
分位数
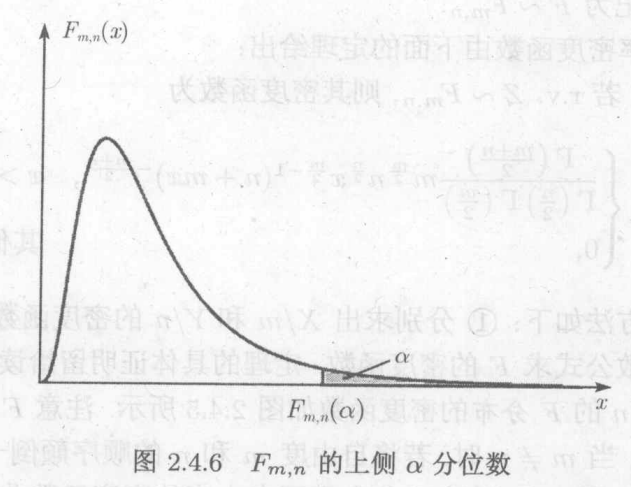
性质:

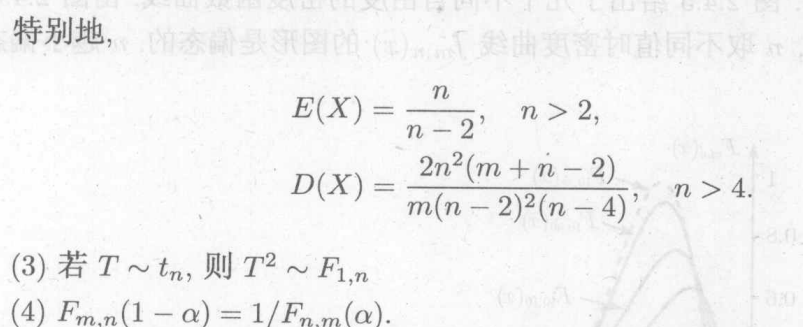
非中心的F分布:
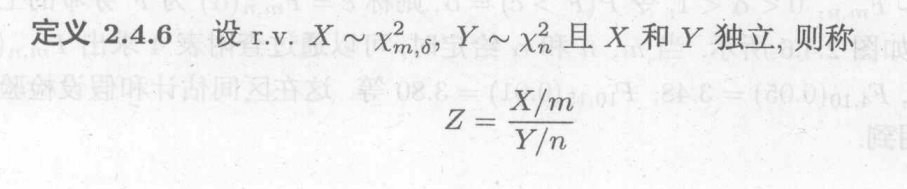


d.几个重要结论
样本服从正态的基本都与有关
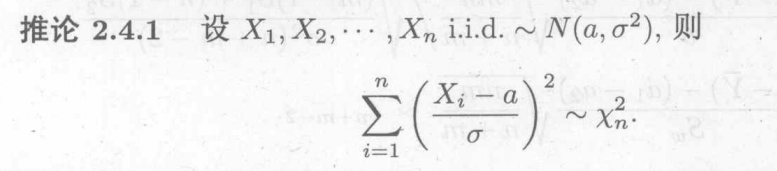
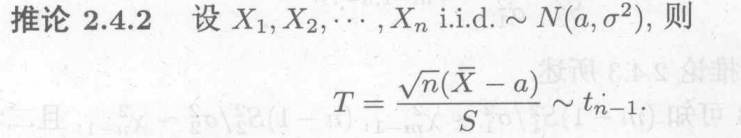
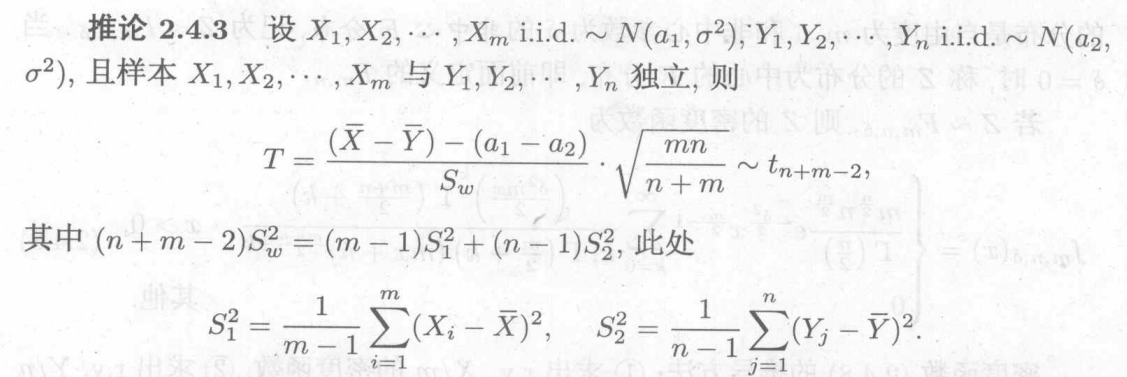
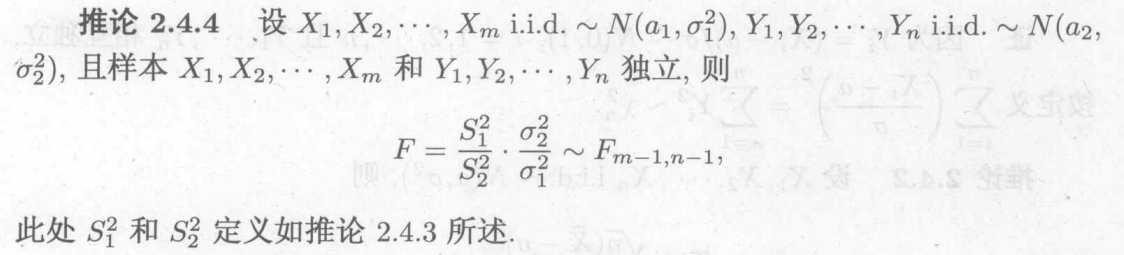
用于方差分析
独立同分布的指数分布的和是卡方分布
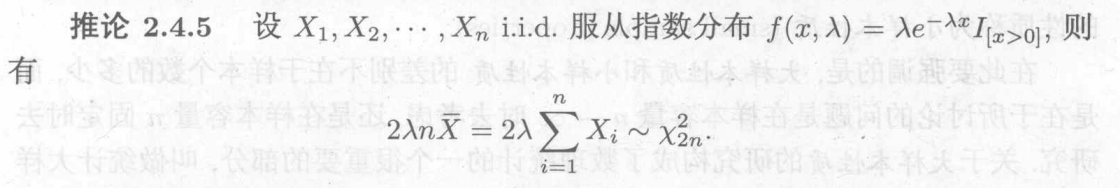
对于取值的讨论:现在一般取
=0.01/
=0.05,但一概而论
的数值会产生一些问题,需要根据具体情况进行讨论,由此会有一个p-value
6.5 统计量的极限分布
大样本性质和小样本性质的差别不在于样本个数的多少,而是在于所讨论的问题是在样本容量时去考虑,还是在样本容量 n 固定时去研究。关于大样本性质的研究构成了数理统计的一个很重要的部分,叫做统计大样本理论。
统计学基础--大数定律、中心极限定理![]() https://zhuanlan.zhihu.com/p/104559816这些都是大样本性质
https://zhuanlan.zhihu.com/p/104559816这些都是大样本性质
无偏性即为小样本性质





6.6 充分统计量

精确定义:

统计量T是对原样本的压缩,但是是无损压缩,即包含了恢复参数所需要的全部信息,也即T的分布中所包含的
的信息
条件概率密度函数:
参数信息的两步:
1)判断统计量T中的参数的信息
2)判断在给定统计量T分布下,X分布的参数信息
当信息只包含在第一步时,称为充分统计量
用熵(entropy)来进行表示:
又
故
判断的充要条件:概率函数

例1:(离散型)

分子不任取是因为给定了x1,...,xn的取值,而分母任取是因为不确定取值

例2:(连续型一个统计量)一对一的


即为,X与Y是一一对应的变换,故对X的操作可以改变为对Y的操作。
根据定义:正交变换后可以使条件概率密度计算更加方便

对于上面的黄色解释:,所以也可以用
与
独立,所以条件密度为n-1个正态分布之积,所以与参数
无关,故为充分统计量。
引申:取,谁好算就用谁

充分统计量不唯一,有下面的引理:

如严格单调递增或严格单调递减,一一对应

例3:(连续型两个统计量)因子分解定理的应用



拓展:服从上的均匀分布,那么
为充分统计量

例4:(连续型三个统计量)

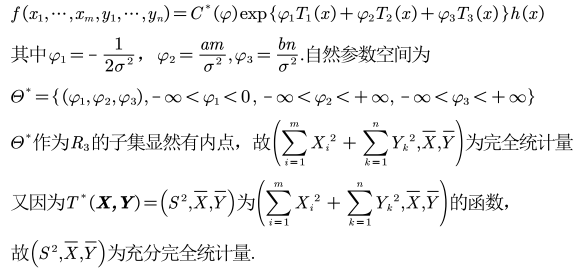
指数族形式——>指数族的自然形式
6.7 指数族

矩阵形式就是:
指数分布族中的T一定是充分统计量,参见因子分解定理

指数族中所有分布具有共同的支撑集,,所以h(x) > 0.
支撑集(support set)是在给定条件下,使得某个函数或集合非零或有意义的那些输入值的集合。这个概念在数学、统计学和优化问题中都有应用。
例1:连续

例2:连续
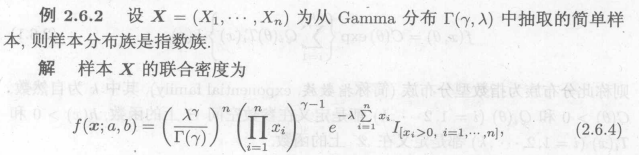

例3:离散

例4:离散
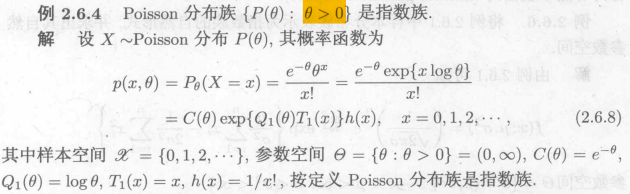
例5:不是指数分布族

均匀分布:,故不是

6.8 指数族的自然形式和极小充分统计量
指数族的自然形式:

如何变换?
对于一般指数族:
令
若与
有一一对应的关系,(即
),则反解
,代入原式得
例1:

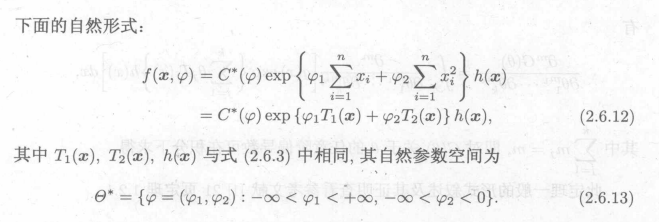
例2:


极小充分统计量:
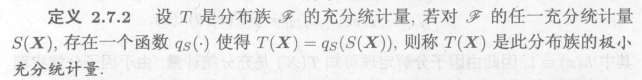
原始的样本数据也是充分统计量,即没有经过压缩
极小充分统计量就是不能再压缩
例:

完全充分统计量:

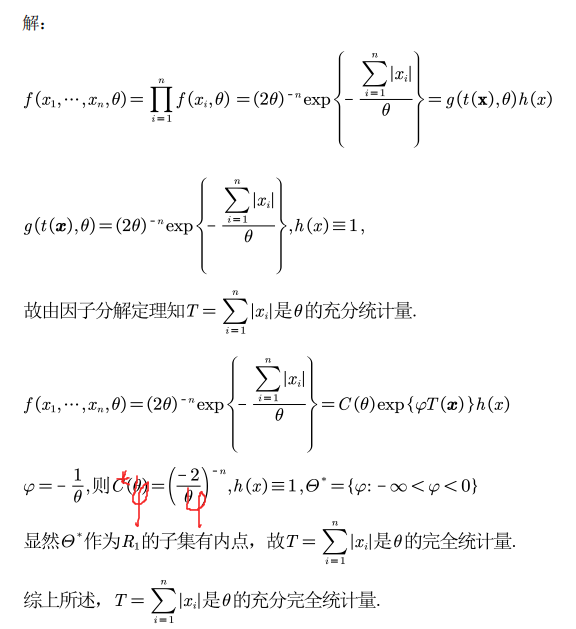
6.9 完全统计量

即不能再将统计量进行变换,即不能再压缩
利用期望的定义:即统计量的分布族函数是完备的,完备的正交函数集

例1:
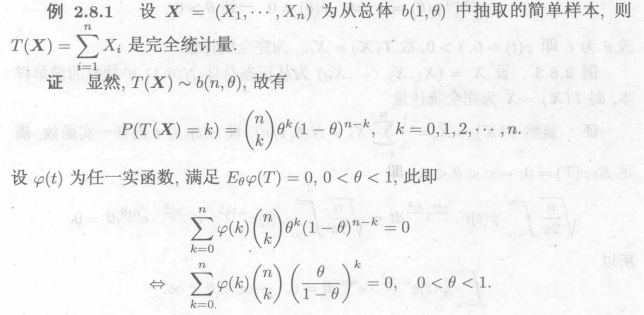

例2:
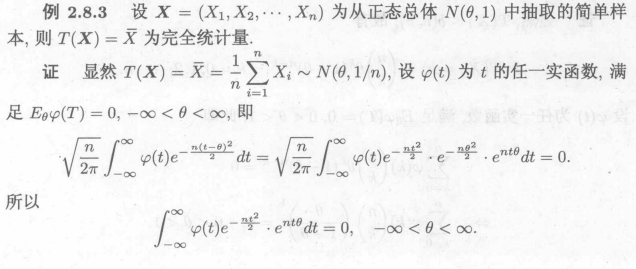

例3:
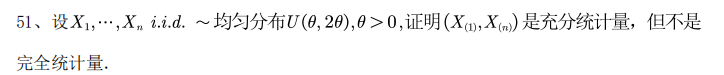

例4:


6.10 指数族中统计量的完全性
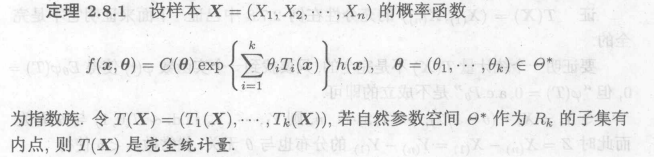
若指数族可以写成指数族的自然形式,则统计量为充分完全统计量
tips:指数族本身写出来就已经是充分统计量了(因子分解定理),又能够写成自然形式,故为完全充分统计量。
内点:在一个集合内部


6.11 有界完全统计量


6.12 在完全充分条件下的独立
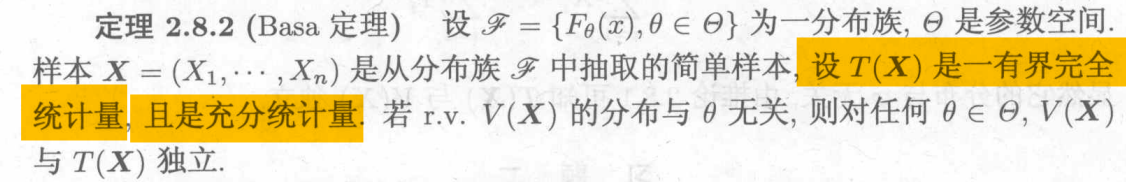
例:(构造变换)

例:

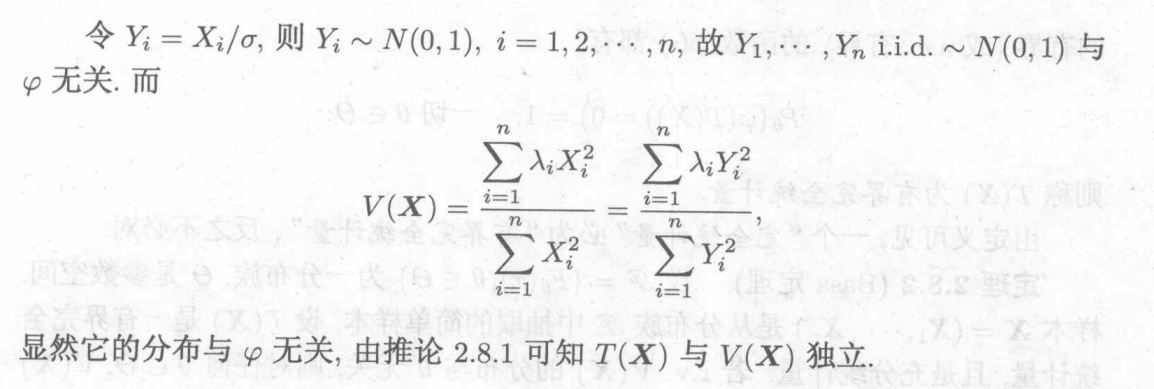
6.13 比较
充分统计量,指数族的自然形式,极小充分统计量,完全统计量的比较:
充分的意思是指包含全部信息,完全的意思是指不能再被压缩
a.一个统计量为充分统计量但不一定是完全统计量
b.充分完全统计量一定是极小充分统计量,反之不一定成立
c.完全统计量一定是有界完全统计量,反之不一定成立
6.14 总结
统计量的充分性:包含完全的未知参数的信息
定义:条件概率分布没有未知参数
因子分解定理——>判断统计量的充分性g(h(T(x)),)*h(x)
指数族是天然的因子分解定理,故满足完全性,即为
统计量的完全性:统计量有没有被压缩完全
定义:若统计量的函数的期望=0,则这些函数=0
指数族的自然形式——>统计量的完全性
在完全充分条件下的独立,完全充分统计量与不与为参数有关的位置参数独立





















 1174
1174

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








