GAMES301---曲面参数化---学习笔记

首先，真的很感谢刘利刚，陈仁杰，傅孝明，方清等各位老师开了GAMES 301课程：《曲面参数化》，让我们能更系统的了解这方面的知识！

一、曲面参数化及其应用

曲面参数化简单解释：3D曲面展开成2D平面
曲面参数化数学本质：3D曲面在2D平面的嵌入/映射（构建曲面到平面区域的一一对应，3D曲面本质是2D的：2D流形）

参数化应用：1、地图制作；2、曲面贴图；3、纹理地图；4、曲线拟合；5、曲面渲染...

二、曲面参数化的表达及度量

参数化基本方法：化繁为简
 1. 函数的简化：假设映射函数为线性函数，将问题转化为基函数的线性组合系数的求解
 2. 定义域的简化：将定义域简化为简单区域（比如三角形，分片三角形为线性的）的拼接，然后在三角形上定义简单函数（有限元方法）---即分片线性逼近
 （1、线性函数：分片线性函数，光滑性低（）；2、高阶多项式函数：分片多项式函数，光滑性较高（）;）

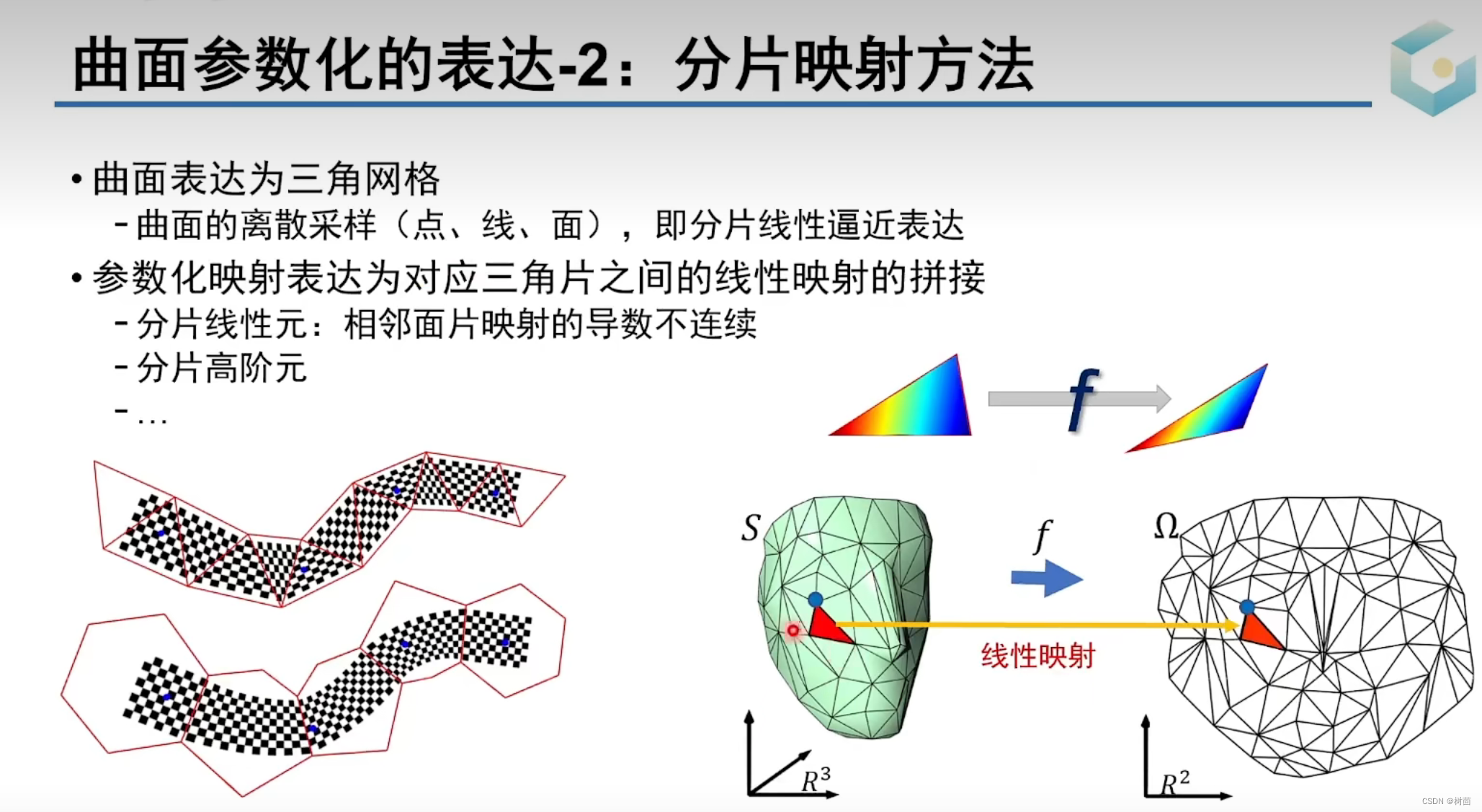
雅克比（Jacobian）矩阵作用：度量局部的变形量
若雅克比行列式为1表示x点没有被拉扯，若大于1表示局部有拉伸，若小于1表示局部有收缩；
若雅可比行列式小于0则局部发生了翻转，若大于0则未翻转。

其他保持不同几何性质的映射：
1、保角映射（共形映射）；（空间曲线在交点处的夹角的计算方法：切线之间的角度）
（共形因子作用：度量在保角映射下曲面局部的伸缩量；Yamabe方程：表示一个曲面高斯曲率的变化）
2、保面积映射（等积映射）；
3、等级映射（即保持面积又保持角度；若一个曲面每个点均可等距映射则此曲面为可展曲面）；

（经证明：可占曲面只有以上三种曲面）
几何形变的度量方法：（图中表示x点的雅克比矩阵行列式，L为对进行SVD分解，、为的奇异值）

（将作为分母，可保证其不接近于0，避免翻转） 

 保持局部双射（即单射，即不发生翻转）的条件：雅克比行列式大于零。

此外注意全局双射等于局部双射，但局部双射并不能推导出全局双射。

“好”参数化的判断条件：1、扭曲小 ；2、无翻转（单射，甚至双射，无鬼影，无全局自交）

三、曲面参数化的主要计算方法

曲面参数化主要方法：

1、线性方法：Tutte’s method (高扭曲，无翻，边界为凸既可以实现无翻转) and its variants

2、优化方法：Geometry-based optimization methods

（ABF/ABF++：保角，不能保证无翻）

(ARAP：保持三角映射的旋转分量（刚性），但不能保证无翻转)

（SA：改用边作为基本单元，但不能保证无翻）

3、保证无翻转的优化方法：Foldover free guaranteed optimization methods

 

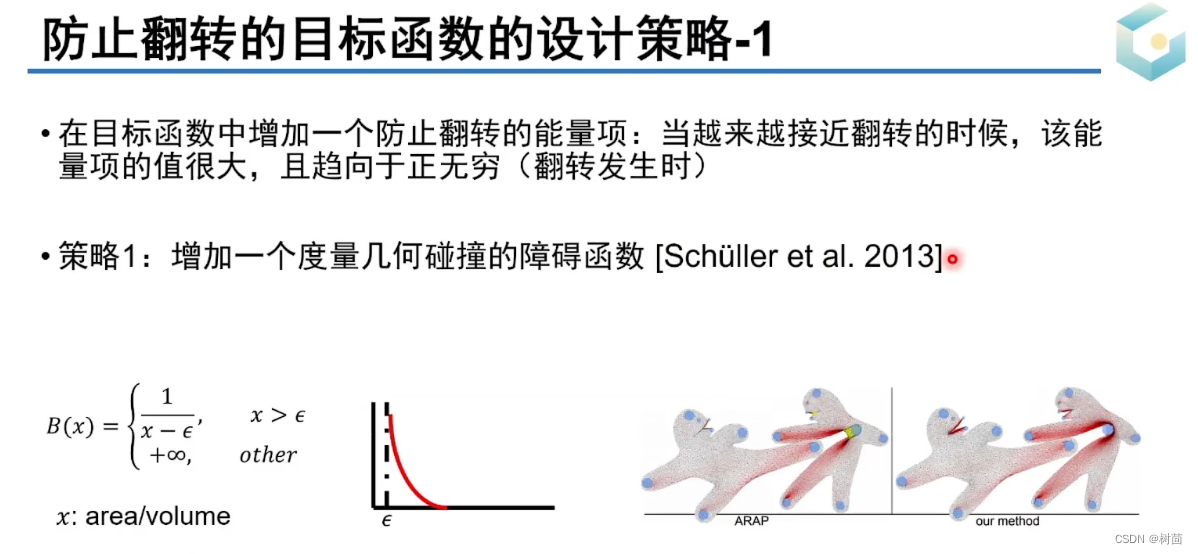
(得到保证无翻，且形变越大能量越大的能量函数，即原问题到此转化为了如何使优化能量函数更小的问题即转变为了单纯的优化问题) 

（H为单位阵则为梯度下降方法，H为Heissian阵则为牛顿法（但计算慢））

1、线性优化方法：（收敛慢，但好算） 

（AQP、SLIM：用拉普拉斯近似Heissian阵）

（AKVF：用向量场是算子近似Heissian阵）

 2、拟牛顿法：

 

 3、牛顿法：（两阶，收敛快，但计算慢）

（PP：给出参考三角形，使扭曲有上界，更改目标函数使目标函数更易解且目标函数不断逼近原本的目标函数）

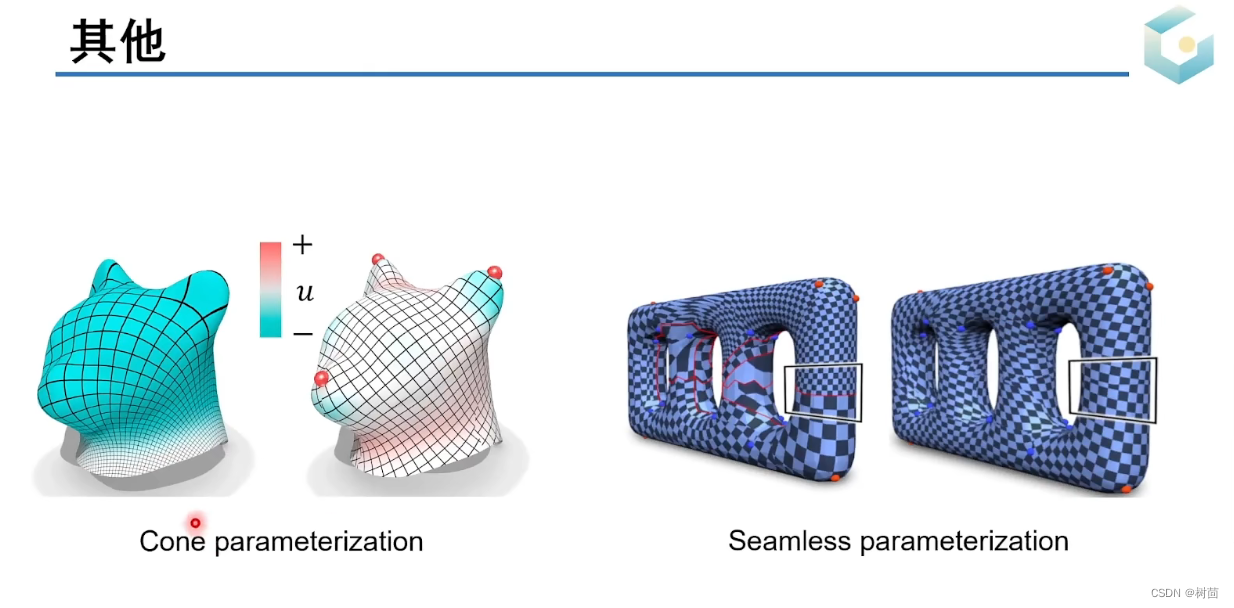
 四、广义参数化及数据降维

球面参数化(Spherical parameterization)：构建封闭曲面与球面的映射（一一映射）

 相容性网格(Compatible mesh): 构建两个曲面之间的映射（一一对应）

 体参数化(Volumetric parameterization):(用四面体剖分整个实体模型，将三角形的仿射变换转变为四面体的仿射变换)

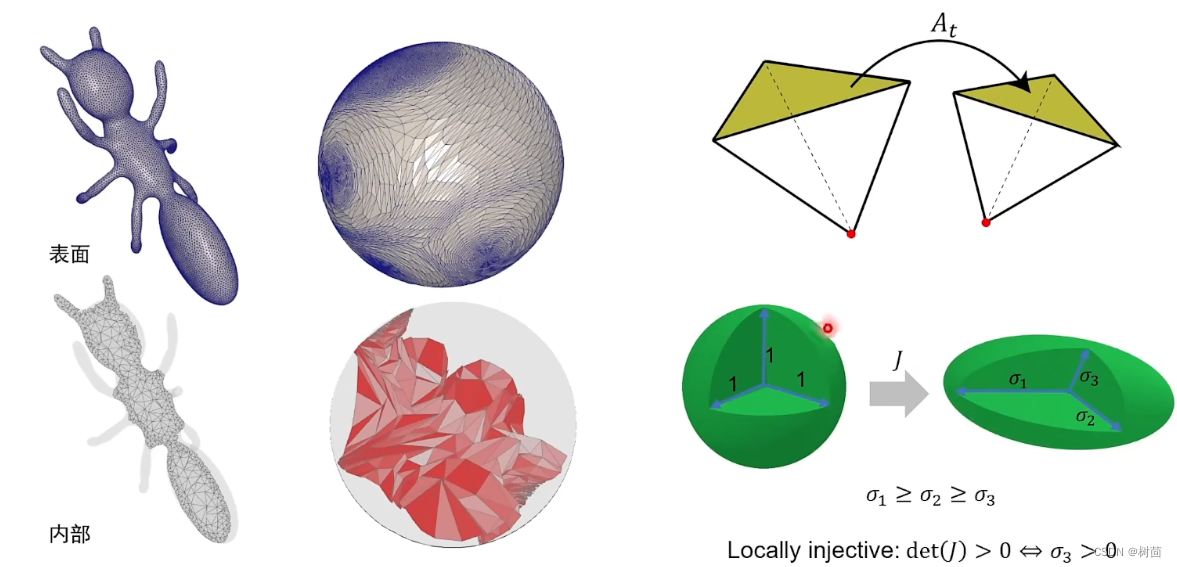
 几何映射(Geometric mapping)：

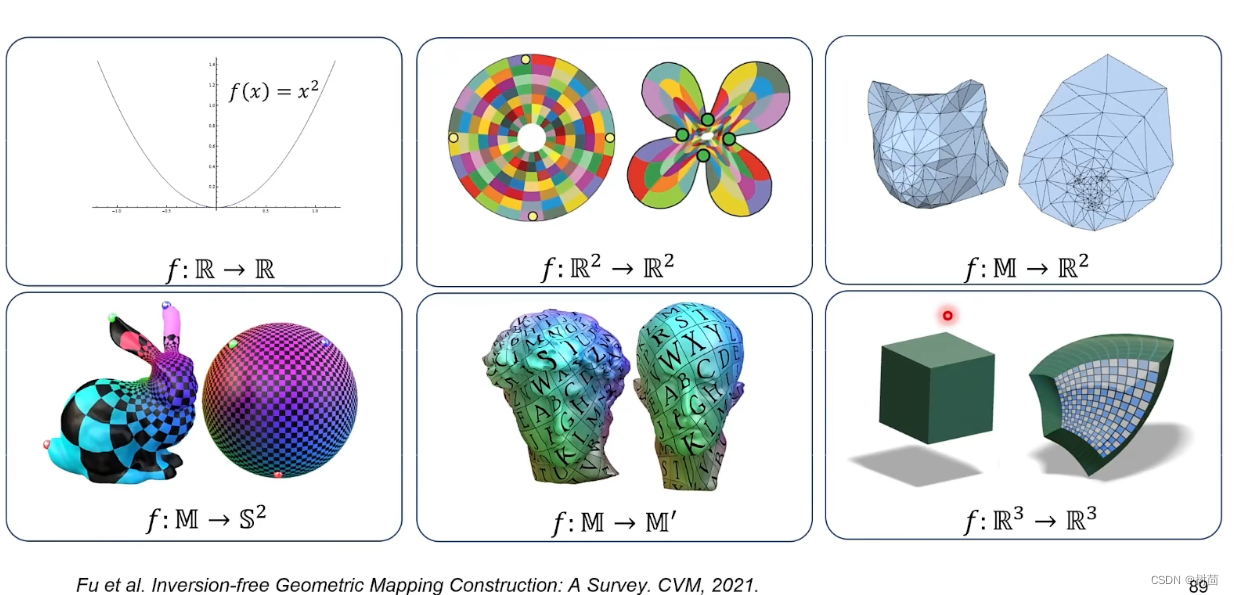
 回顾：参数曲面(Parametric surfaces）概念:（高维数据可用本征维度表达，参数就是本征维度）

 本征维度：相互独立的变量的个数（本征维度才是研究数据对象的本质上的处理手段）

 参数化的本质：低维嵌入，降维映射一般会丢失一些信息，此信息无法恢复。

流形学习、降维：给定一个高维数据，去寻找它的本征维度。（高维数据的参数化）

 

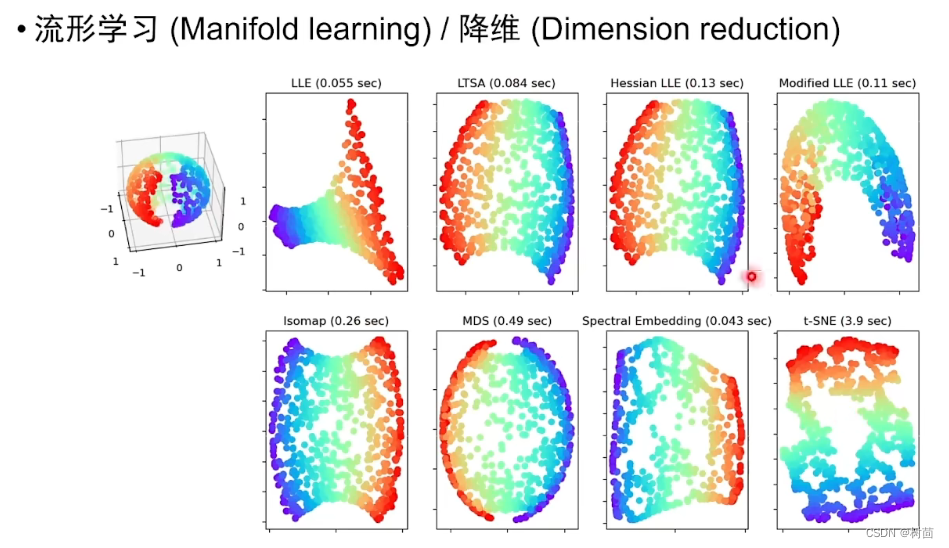
寻找本征维度方法：

 （最中间的latent code参数一定不能低于本征维度，如果低于会丢失很多信息）

小结

 低维到高维的拟合要用到位置编码（使用傅里叶展开将低维信息编码到高维，再去做拟合） 可抓到原细节