半导体中载流子的统计分布

凉月松心

已于 2022-10-04 19:40:18 修改

阅读量2.1k

点赞数 3

分类专栏：半导体物理文章标签：制造

于 2022-10-03 13:54:00 首次发布

本文链接：https://blog.csdn.net/m0_52555753/article/details/127150645

版权

半导体物理专栏收录该内容

24 篇文章

订阅专栏

回顾：半导体是一种自身性质容易受到外界影响的物质，半导体的导电能力会随着外界因素变化而显著变化，载流子的浓度和运动能力的强弱是两个关键因素，影响导电能力

因为电子空穴是大量的微观电子，用统计的方法，分布函数来计算

T一定并且没有外加因素的情况下，载流子的来源

（1）价带底的电子可以跃迁，价带电子跃迁到导带，称为导带中的导电电子（这个就是所谓的本征激发）这个过程的相反过程同时存在，这是导电电子的一种来源

（2）电子也可以来源于施主杂质的电离，这个过程的相反过程也同时存在

=》可以达到一种动态的平衡，导带的电子浓度 $n_0$ ，价带的空穴浓度 $p_0$ 称为热平衡态

第三章我们要解决两个问题

（1）怎么计算导带的电子浓度 $n_0$ 和价带的空穴浓度 $p_0$

（2）解决温度变化时的半导体中的载流子浓度的变化规律

要计算导带的电子浓度，导带是能量允许区间，我们可以认为能带是准连续的

单位能量间隔里面有多少电子可以呆的地方，这些可以呆的地方也不一定全部排满，能量越高，占据的可能性越小

怎么计算导带的电子浓度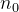 $n_0$ 和价带的空穴浓度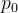 $p_0$

先解决有多少可以呆的地方？

单位能量间隔有多少量子态数？

状态密度：由于导带和价带是准连续的，因此定义单位能量间隔内的量子态数为状态密度

$\small g(E)=\frac{dZ}{dE}$ ，为了求出状态密度，我们按照这么几个步骤来求

1.求出K空间的量子态密度

2.求能量为E的等能面在K空间所围成的体积

3.（1）*（2）就是等能面里面所围的量子态数

K空间的取值 $\small k_x=\frac{n_x}{L_1},k_y=\frac{n_y}{L_2},k_z=\frac{n_z}{L_3}$ ,波矢K的取值只能这么取，波矢k的取值在K空间均匀分布

每个允许的k值，在k空间所占的体积 $\small =\frac{1}{L_1 \times L_2 \times L_3 }=\frac{1}{V}$

所以K空间量子态密度 $\small =\frac{1}{\frac{1}{V}}=V$ ，考虑到自旋所以就是 $\small 2V$

球形等能面 $\small m_n^*$ 各向同性， $\small E-E_c=\frac{h^2}{2m_n^*}(k_x^2+k_y^2+k_z^2)$ ，体积 $\small =\frac{4}{3}\pi k^3=\frac{4}{3} \pi \frac{(2m_n^*)^{\frac{3}{2}}}{h^3}(E-E_c)^{\frac{3}{2}}$

求导带的状态密度， $\small Z(E)=2V \times$ 体积 $\small =2V \cdot \frac{4}{3} \pi \frac{(2m_n^*)^{\frac{3}{2}}}{h^3}(E-E_c)^{\frac{3}{2}}$

按照定义求微分， $\small g_{c}(E)=\frac{4 \pi V}{h^3}(2m_n^*)^{\frac{3}{2}}(E-E_c)^{\frac{1}{2}}$

对硅和锗，电子的 $\small m_n^*$ 各向异性，此时算体积的时候就不一样了

构成了旋转椭球等能面

$\small E-E_c=\frac{h^2}{2}[\frac{(k_x-k_{0x})^2}{m_x^*}+\frac{(k_y-k_{0y})^2}{m_y^*}+\frac{(k_z-k_{0z})^2}{m_z^*}]$ ,有效质量是各向异性，并且极值点不在中心

写成椭球的标准方程

$\small \frac{k_1^2}{\frac{2m_t}{h^2}(E-E_c)}+\frac{k_2^2}{\frac{2m_t}{h^2}(E-E_c)}+\frac{k_3^2}{\frac{2m_l}{h^2}(E-E_c)}=1$

体积= $\small \frac{4}{3} \pi abc=\frac{4}{3} \pi \frac{2m_t(2m_l)^{\frac{1}{2}}}{h^3}(E-E_c)^{\frac{3}{2}}$

这样的旋转椭球共有s个，s=6是硅，s=4是锗

我们把体积和量子态密度一乘 $\small Z(E)=2VS\frac{4}{3} \pi \frac{2m_t(2m_l)^{\frac{1}{2}}}{h^3}(E-E_c)^{\frac{3}{2}}$

在微分一下， $\small g_{c}(E)=\frac{dZ}{dE}=\frac{4 \pi V}{h^3} 2Sm_t(2m_l)^{\frac{1}{2}}(E-E_c)^{\frac{1}{2}}$

如果 $\small (2m_n^*)^{\frac{3}{2}}=2Sm_t(2m_l)^{\frac{1}{2}} \\ ->m_n^*=(S^2m_t^2m_l)^{\frac{1}{3}}$ 此时的有效质量称为导带电子状态密度有效质量

价带状态密度，用下标 $\small g_{v}(E)=\frac{4 \pi V}{h^3}(2m_p^*)^{\frac{3}{2}}(E_v-E)^{\frac{1}{2}},m_p^*=[(m_{ph})^{\frac{3}{2}}+(m_{pl})^{\frac{3}{2}}]^{\frac{2}{3}}$

称 $\small m_p^*$ 为价带空穴状态密度有限质量

费米能级和载流子的统计分布

费米分布函数,电子按照能量分布的规律，一个按照能量为E的独立电子态，被一个电子占据的几率是 $\small f(E)=\frac{1}{1+exp(\frac{E-E_F}{k_0t})}$ 这么大的几率（备注：所谓独立电子态是指不论该电子状态被电子占据与否，均不影响其他影响的占据情况）

分布函数有几个量注意一下， $\small E_F$ 称作费米能级，用电中性条件求得，费米能级有确定的物理意义，在这个表达式里面有一个 $\small K_0$ ，玻尔兹曼常数，我们还有后面一项 $\small T$ ，这个T是绝对温度

T在300k下， $\small k_0T=0.026ev$

我们简单的讨论一下，

1 在费米分布函数里面 $\small T->0k$ ,若 $\small E>E_F$ ， $\small f(E)=0$ ,若 $\small E<E_F$ ， $\small f(E)=1$

$\small T->0 k$ 费米能级是电子填充能量水平的分界线 ,即 $\small E<E_F$ 的能级上，都被电子所占据，而 $\small E>E_F$ 的能级上，都是空的，所以温度很低的时候，费米能级标志了填充情况

2.任意温度下，费米构造的这个分布函数，若若 $\small E>E_F$ ，这个时候 $\small f(E)<\frac{1}{2}$ ，而电子占据的某个能量状态比费米能级低的话， $\small f(E)>\frac{1}{2}$ ,若 $\small E=E_F$ ， $\small f(E_F)=\frac{1}{2}$ ，若 $\small E=E_F+5K_0T$ , $\small f(E_F+5K_0T)=\frac{1}{1+e^5}=0.7%$ ,若 $\small E_F=E_F-5K_0T$ ， $\small f(E_F-5K_0T)=\frac{1}{1+e^{-5}}=99.3%$