TimeDART——结合扩散去噪和自回归建模的时间序列自监督学习框架

放空儿

已于 2025-03-09 21:07:46 修改

阅读量1.3k

点赞数 29

分类专栏：论文分享文章标签：深度学习论文阅读人工智能

于 2025-02-24 16:51:08 首次发布

本文链接：https://blog.csdn.net/m0_57689625/article/details/145824812

版权

论文分享专栏收录该内容

12 篇文章

订阅专栏

原文地址：TimeDART: A Diffusion Autoregressive Transformer for Self-Supervised Time Series Representation

发表会议：暂定

代码地址：GitHub - Melmaphother/TimeDART：这是论文的官方 PyTorch 实现：TimeDART：用于自监督时间序列表示的扩散自回归转换器https://github.com/Melmaphother/TimeDART

作者：汪道玉、程明月（通讯）、刘志定、刘琦、陈恩红

团队：中国科学技术大学

科普：

自监督学习概述：自监督学习是一种创新的学习范式，其特点是模型能够从未标记数据中通过内部生成的监督信号进行学习，通常这种学习通过预文任务来实现。与传统的监督学习不同，自监督学习不需要外部标签，而是利用数据本身的内在结构来创建必要的学习信号。

研究背景：

大多数时间序列数据往往缺乏标注，使得传统的监督学习方法难以广泛应用。但是现有的自监督学习方法虽然有效，但往往难以以统一的方式全面捕捉长期动态演化和微妙的局部模式。

科普：

现有的时间序列自监督方法：

掩码自编码通过重建被掩盖的数据学习时间序列的隐含模式，但容易受到预训练-微调整(pretrain-finetune)不匹配的影响；
对比学习强调样本间相似性，然而它主要针对整体序列进行建模，难以捕捉细粒度的时间动态；
自回归方法遵循时间序列的自然左到右(Left-to-Right)结构，适合长期依赖建模，但容易受噪声误差累积的影响，从而降低预测精度。

在此背景下，时间序列监督学习面临三大挑战：如何同时兼顾全局趋势建模与局部细节捕捉？如何缓解自回归方法对噪声的敏感性？如何提升自监督表示的泛化能力，使其适用于不同的时间序列任务？

所以，本文提出了TimeDART 一种结合因果Transformer编码器和扩散模型的框架，通过自回归生成和扩散去噪联合优化，同时建模时间序列的长期动态演化（全局特征）与局部细节模式（局部特征）。

这里如果需要了解之前三种时间序列自监督的一些代表模型可以去阅读原文的Related Work

扩散模型核心优势包括： 对局部波动模式的高保真重建概率化生成缓解确定性预测偏差

现有局限：

任务局限：当前方法聚焦概率生成任务（如数据补全/合成），直接用于预测等下游任务效果欠佳（Zhang et al., 2024a）
表征缺陷：过度关注整体序列生成质量，忽略局部细粒度模式的语义保持、

TimeDART方法讲解（重点）

TimeDART是一种专为时间序列预测设计的自监督学习方法。它的核心思想是通过从时间序列历史数据中学习模式来改进未来数据点的预测。研究者采用了一种创新的方法，将时间序列数据分解成更小的片段（patches），并将这些patches作为建模的基本单位。

核心技术组件

Transformer编码器设计：- 使用了具有自注意力机制的Transformer编码器- 专注于理解patches之间的依赖关系- 有效捕获数据的整体序列结构
扩散和去噪过程：- 实现了两个关键过程：扩散和去噪- 通过向数据添加和移除噪声来捕获局部特征- 这是所有扩散模型中的典型过程- 提升了模型在详细模式上的表现

TimeDART架构图展示了模型如何：

使用自回归生成捕获全局依赖关系
通过去噪扩散模型处理局部结构
在前向扩散过程中向输入patches引入噪声
生成自监督信号
通过自回归方式在反向过程中恢复原始序列

实例归一化和Patch嵌入

关键步骤：

实例归一化：- 对输入的多变量时间序列数据进行标准化- 确保每个实例具有零均值和单位标准差- 目的是保持最终预测的一致性
数据分割策略：- 将时间序列数据划分为patches而非单个点- 这种方法能够捕获更全面的局部信息
避免信息泄漏：- patch长度设置为等于stride（步长）- 确保每个patch包含原始序列的非重叠段- 防止训练过程中的信息泄漏

Transformer编码器中的Patch间依赖关系

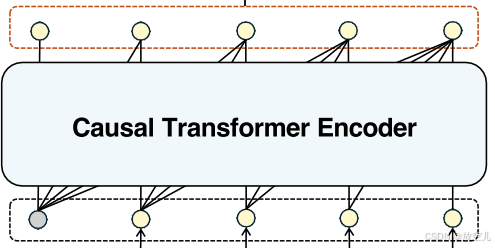
关键特性：

基于自注意力的处理：- 使用自注意力的Transformer编码器- 专门用于建模patches之间的依赖关系
全局依赖性捕获：- 通过考虑时间序列数据中不同patches之间的关系- 有效捕获全局序列依赖关系
表示学习：- Transformer编码器能够学习有意义的patch间表示- 这对于理解时间序列的高层结构至关重要

SOS和位置编码：

$z_{1:N}^{\text{in}} = \text{Concat}[SOS, z_{1:N-1}] + PE_{1:N},$

$z_{1:N}^{\text{in}}$ 是输入到编码器的序列，包括SOS（start-of-sequence）嵌入和位置编码。

$z_{1:N-1}$ 是前 $N-1$ 个分块的嵌入。

$PE_{1:N}$ 是位置编码。

编码器处理：

$f(z_{1:N}^{\text{in}}) = \text{Encoder}(z_{1:N}^{\text{in}}, M),$

$f(z_{1:N}^{\text{in}})$ 是编码器的输出，经过因果掩码 $M$ 处理后的上下文化表示。

 classTransformerEncoderBlock(nn.Module):
     def__init__(
         self, d_model: int, num_heads: int, feedforward_dim: int, dropout: float
     ):
         super(TransformerEncoderBlock, self).__init__()

         self.attention=nn.MultiheadAttention(
             embed_dim=d_model, num_heads=num_heads, dropout=dropout, batch_first=True
         )
         self.norm1=nn.LayerNorm(d_model)
         self.ff=nn.Sequential(
             nn.Linear(d_model, feedforward_dim),
             nn.GELU(),
             nn.Dropout(dropout),
             nn.Linear(feedforward_dim, d_model),
         )
         self.conv1=nn.Conv1d(in_channels=d_model, out_channels=feedforward_dim, kernel_size=1)
         self.activation=nn.GELU()
         self.conv2=nn.Conv1d(in_channels=feedforward_dim, out_channels=d_model, kernel_size=1)
         self.norm2=nn.LayerNorm(d_model)
         self.dropout=nn.Dropout(dropout)

     defforward(self, x, mask):
         """
         :param x: [batch_size * num_features, seq_len, d_model]
         :param mask: [1, 1, seq_len, seq_len]
         :return: [batch_size * num_features, seq_len, d_model]
         """
         # Self-attention
         attn_output, _=self.attention(x, x, x, attn_mask=mask)
         x=self.norm1(x+self.dropout(attn_output))

         # Feed-forward network
         # y = self.dropout(self.activation(self.conv1(y.permute(0, 2, 1))))
         # ff_output = self.conv2(y).permute(0, 2, 1)
         ff_output=self.ff(x)
         output=self.norm2(x+self.dropout(ff_output))

         returnoutput

前向扩散过程

主要特点：

噪声应用：- 在输入patches上应用噪声- 生成自监督信号- 通过从带噪声版本中重构原始数据来学习稳健的表示
模式识别：- 噪声帮助模型识别和关注- 专注于时间序列数据中的内在模式

前向过程：

定义：前向过程 $q(x_j^s|x_j^{s-1})$ 是一个高斯分布。

均值： $\sqrt{\alpha(s)}x_j^{s-1}$
方差： $(1-\alpha(s))I$

参数说明： $\alpha(s)$ 控制每一步的噪声水平。

累积乘积： $\gamma(s) = \prod_{s' \leq s} \alpha(s')$

重写前向过程： $q(x_j^s|x_j^0) = \mathcal{N}(x_j^s; \sqrt{\gamma(s)}x_j^0, (1-\gamma(s))I)$

解释： $x_j^0$ 是原始的干净图像块，每个图像块在时间步 $s$ 独立地添加噪声。

噪声图像块表示： $\hat{x}_{1:N} = [x_1^{s^1}, \ldots, x_N^{s^N}]$

噪声调度器与嵌入层：

噪声调度器：使用余弦调度方法设置噪声调度器 $\alpha(s)$ ： $\alpha(s) \propto \cos\left(\frac{s}{T}\pi\right)$

优势：与线性递减方法相比，提供更平滑的过渡，强调扩散过程的早期和后期阶段，提高模型的稳定性和数据分布的捕捉能力。

嵌入层与位置编码：

共享嵌入层和权重：噪声和干净图像块共享相同的嵌入层和权重。
正弦位置编码： $\hat{z}_{1:N}^{\text{in}} = \text{Embedding}(\hat{x}_{1:N}) + PE_{1:N}$

解释： $\hat{z}_{1:N}^{\text{in}}$ 表示噪声图像块的嵌入表示， $PE_{1:N}$ 是正弦位置编码，用于保留位置信息。

 classDiffusion(nn.Module):
     def__init__(
         self,
         time_steps: int,
         device: torch.device,
         scheduler: str="cosine",
     ):
         super(Diffusion, self).__init__()
         self.device=device
         self.time_steps=time_steps

         ifscheduler=="cosine":
             self.betas=self._cosine_beta_schedule().to(self.device)
         elifscheduler=="linear":
             self.betas=self._linear_beta_schedule().to(self.device)
         else:
             raiseValueError(f"Invalid scheduler: {scheduler=}")

         self.alpha=1-self.betas
         self.gamma=torch.cumprod(self.alpha, dim=0).to(self.device)

     def_cosine_beta_schedule(self, s=0.008):
         steps=self.time_steps+1
         x=torch.linspace(0, self.time_steps, steps)
         alphas_cumprod= (
             torch.cos(((x/self.time_steps) +s) / (1+s) *torch.pi*0.5) **2
         )
         alphas_cumprod=alphas_cumprod/alphas_cumprod[0]
         betas=1- (alphas_cumprod[1:] /alphas_cumprod[:-1])
         returntorch.clip(betas, 0, 0.999)

     def_linear_beta_schedule(self, beta_start=1e-4, beta_end=0.02):
         betas=torch.linspace(beta_start, beta_end, self.time_steps)
         returnbetas

     defsample_time_steps(self, shape):
         returntorch.randint(0, self.time_steps, shape, device=self.device)

     defnoise(self, x, t):
         noise=torch.randn_like(x)
         gamma_t=self.gamma[t].unsqueeze(-1)  # [batch_size * num_features, seq_len, 1]
         # x_t = sqrt(gamma_t) * x + sqrt(1 - gamma_t) * noise
         noisy_x=torch.sqrt(gamma_t) *x+torch.sqrt(1-gamma_t) *noise
         returnnoisy_x, noise

     defforward(self, x):
         # x: [batch_size * num_features, seq_len, patch_len]
         t=self.sample_time_steps(x.shape[:2])  # [batch_size * num_features, seq_len]
         noisy_x, noise=self.noise(x, t)
         returnnoisy_x, noise, t

基于交叉注意力的去噪解码器

特点：

核心功能：- 使用交叉注意力机制- 目的是重构原始的、无噪声的patches
优化设计：- 允许可调整的优化难度- 使自监督任务更有效- 使模型能够专注于捕获详细的patch内特征

解码器的工作机制：

接收噪声（作为查询）和编码器的输出（键和值）
使用掩码确保第j个噪声输入对应于Transformer编码器的第j个输出

在因果遮蔽（causal mask）的指导下，位置 $j$ 处的编码器输出聚合了位置 $1$ 到 $j-1$ 处干净patch的信息，从而实现了自回归优化。最后，通过线性投影将深层表示映射回原始空间。反向过程可以表示为：

$z_j^{\text{out}} = g(z_j^{\text{in}}, f(z_{1:j-1}^{\text{in}})), \quad 1 \leq j \leq N,$

其中 $g(\cdot)$ 表示去噪解码器对编码器输出和加噪patch嵌入的处理。

 classTransformerDecoderBlock(nn.Module):
     def__init__(
         self, d_model: int, num_heads: int, feedforward_dim: int, dropout: float
     ):
         super(TransformerDecoderBlock, self).__init__()

         self.self_attention=nn.MultiheadAttention(
             embed_dim=d_model, num_heads=num_heads, dropout=dropout, batch_first=True
         )
         self.norm1=nn.LayerNorm(d_model)
         self.encoder_attention=nn.MultiheadAttention(
             embed_dim=d_model, num_heads=num_heads, dropout=dropout, batch_first=True
         )
         self.norm2=nn.LayerNorm(d_model)
         self.ff=nn.Sequential(
             nn.Linear(d_model, feedforward_dim),
             nn.ReLU(),
             nn.Dropout(dropout),
             nn.Linear(feedforward_dim, d_model),
         )
         self.norm3=nn.LayerNorm(d_model)
         self.dropout=nn.Dropout(dropout)

     defforward(self, query, key, value, tgt_mask, src_mask):
         """
         :param query: [batch_size * num_features, seq_len, d_model]
         :param key: [batch_size * num_features, seq_len, d_model]
         :param value: [batch_size * num_features, seq_len, d_model]
         :param mask: [1, 1, seq_len, seq_len]
         :return: [batch_size * num_features, seq_len, d_model]
         """
         # Self-attention
         attn_output, _=self.self_attention(query, query, query, attn_mask=tgt_mask)
         query=self.norm1(query+self.dropout(attn_output))

         # Encoder attention
         attn_output, _=self.encoder_attention(query, key, value, attn_mask=src_mask)
         query=self.norm2(query+self.dropout(attn_output))

         # Feed-forward network
         ff_output=self.ff(query)
         x=self.norm3(query+self.dropout(ff_output))

         returnx

用于全局依赖关系的自回归生成

自回归生成的主要职责：

高层依赖捕获：- 捕获时间序列中的高层全局依赖关系- 通过自回归方式恢复原始序列- 使模型能够理解整体时间模式和依赖关系- 显著提升预测能力

 classDenoisingPatchDecoder(nn.Module):
     def__init__(
         self,
         d_model: int,
         num_heads: int,
         num_layers: int,
         feedforward_dim: int,
         dropout: float,
     ):
         super(DenoisingPatchDecoder, self).__init__()

         self.layers=nn.ModuleList(
             [
                 TransformerDecoderBlock(d_model, num_heads, feedforward_dim, dropout)
                 for_inrange(num_layers)
             ]
         )
         self.norm=nn.LayerNorm(d_model)

     defforward(self, query, key, value, is_tgt_mask=True, is_src_mask=True):
         seq_len=query.size(1)
         tgt_mask= (
             generate_self_only_mask(seq_len).to(query.device) ifis_tgt_maskelseNone
         )
         src_mask= (
             generate_self_only_mask(seq_len).to(query.device) ifis_src_maskelseNone
         )
         forlayerinself.layers:
             query=layer(query, key, value, tgt_mask, src_mask)
         x=self.norm(query)
         returnx


 classForecastingHead(nn.Module):
     def__init__(
         self,
         seq_len: int,
         d_model: int,
         pred_len: int,
         dropout: float,
     ):
         super(ForecastingHead, self).__init__()
         self.pred_len=pred_len
         self.flatten=nn.Flatten(start_dim=-2)
         self.forecast_head=nn.Linear(seq_len*d_model, pred_len)
         self.dropout=nn.Dropout(dropout)

     defforward(self, x: torch.Tensor) ->torch.Tensor:
         """
         :param x: [batch_size, num_features, seq_len, d_model]
         :return: [batch_size, pred_len, num_features]
         """
         x=self.flatten(x)  # (batch_size, num_features, seq_len * d_model)
         x=self.forecast_head(x)  # (batch_size, num_features, pred_len)
         x=self.dropout(x)  # (batch_size, num_features, pred_len)
         x=x.permute(0, 2, 1)  # (batch_size, pred_len, num_features)
         returnx

自监督优化目标是通过最小化扩散损失来实现的，这个扩散损失等价于证据下界（ELBO）。具体的损失函数公式为：

$\mathcal{L}_{\text{diff}} = \sum_{j=1}^{N} \mathbb{E}_{\epsilon, q(x_j^0)} \left[ \left\| x_j^0 - g(\hat{z}_j^{\text{in}}, \, f(z_{1:j-1}^{\text{in}})) \right\|^2 \right].$