【优化算法比较】‘ABC‘,‘GA‘,‘PSO‘,‘SSA‘,‘GWO‘,‘CSO‘,‘DBO‘,‘BWO‘,‘DE‘,‘OBLDE‘优化算法比较（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

2.1 CEC2005测试函数

2.2 CEC2017测试函数

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

以下是对这些算法的简要比较：

1. ABC（人工蜂群算法）：基于蜜蜂觅食行为的优化算法，具有较好的全局搜索能力和收敛速度。

2. GA（遗传算法）：基于生物进化过程的优化算法，适用于复杂的优化问题，但可能陷入局部最优解。

3. PSO（粒子群优化算法）：模拟鸟群觅食行为的优化算法，易于实现和调整，但可能受到参数选择的影响。

4. SSA（萤火虫算法）：模拟萤火虫求爱行为的优化算法，具有较好的全局搜索性能和收敛速度。

5. GWO（灰狼优化算法）：模拟灰狼群协作狩猎行为的优化算法，具有较好的全局搜索性能和收敛速度。

6. CSO（细菌觅食算法）：模拟细菌觅食行为的优化算法，适用于连续优化问题，但可能受到参数选择的影响。

7. DBO（混沌蝗虫优化算法）：基于混沌理论和蝗虫觅食行为的优化算法，具有较好的全局搜索性能和收敛速度。

8. BWO（蝇虫优化算法）：模拟蝇虫觅食行为的优化算法，适用于复杂优化问题，但可能受到参数选择的影响。

9. DE（差分进化算法）：基于个体差异和群体协作的优化算法，适用于连续优化问题，但可能收敛速度较慢。

10. OBLDE（基于优势学习的差分进化算法）：结合了优势学习机制的差分进化算法，具有较好的收敛速度和全局搜索性能。

综合来看，不同算法适用于不同类型的优化问题，在选择算法时需要根据具体问题特点和算法性能进行综合考虑。

📚2 运行结果

2.1 CEC2005测试函数

2.2 CEC2017测试函数

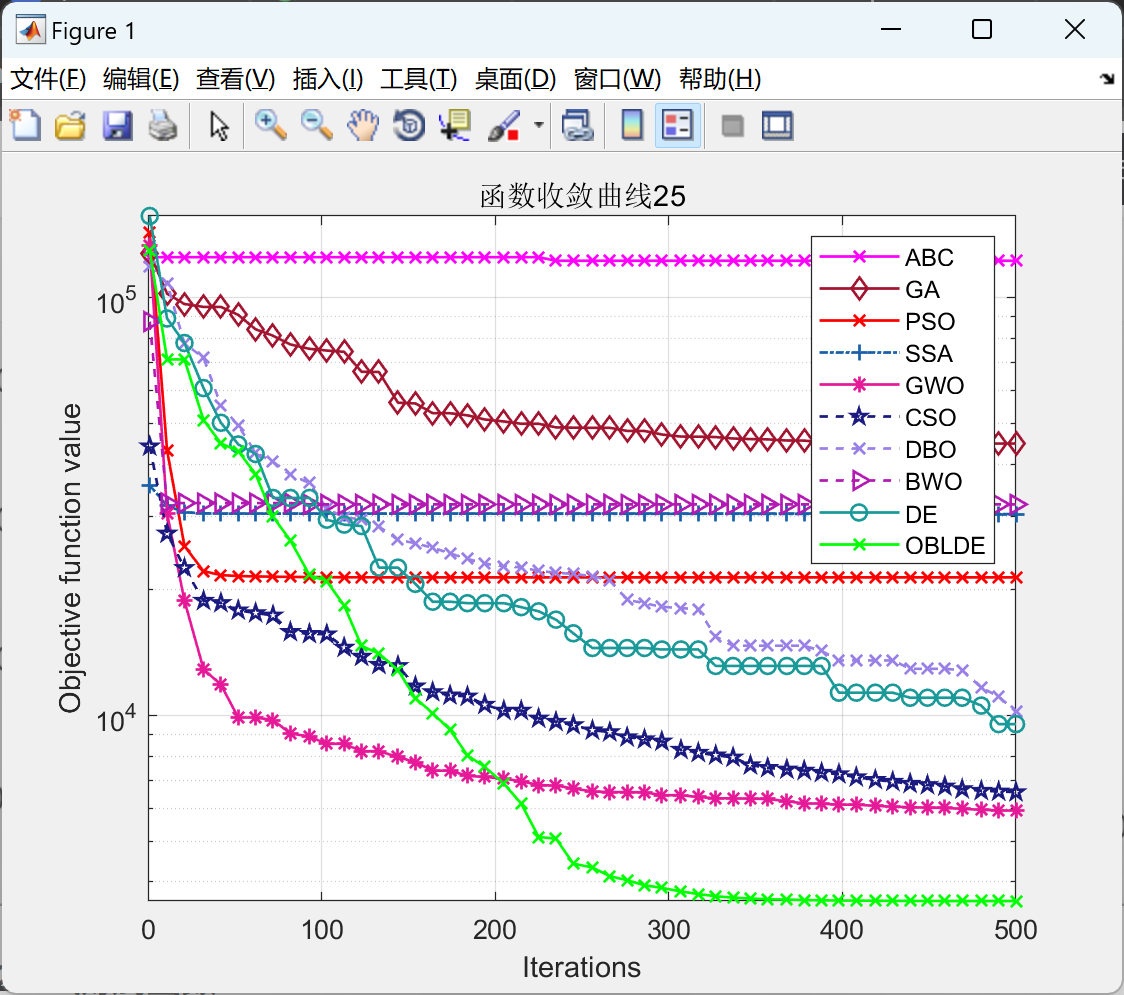
部分代码：

iter=1:1:T;
semilogy(iter(k),ABC_trace(k),'m-x','linewidth',1);
hold on
semilogy(iter(k),GA_trace(k),'Color',[0.6350 0.0780 0.1840],'Marker','d','LineStyle','-','linewidth',1);
hold on
semilogy(iter(k),pso_curve(k),'r-x','linewidth',1);
hold on
semilogy(iter(k),SSA_curve(k),'Color',[0.1 0.3780 0.66],'Marker','+','LineStyle','-.','linewidth',1);
hold on
semilogy(iter(k),GWO_curve(k),'Color',[0.9 0.1 0.6],'Marker','*','LineStyle','-','linewidth',1);
hold on
semilogy(iter(k),cso_trace(k),'Color',[0.1 0.1 0.5],'Marker','p','LineStyle','--','linewidth',1);
hold on
semilogy(iter(k),DBO_curve(k),'Color',[0.6 0.5 0.9],'Marker','x','LineStyle','--','linewidth',1);
hold on
semilogy(iter(k),BWO_curve(k),'Color',[0.7 0.1 0.7],'Marker','>','LineStyle','--','linewidth',1);
hold on
semilogy(iter(k),DE_curve(k),'Color',[0.1 0.6 0.6],'Marker','o','LineStyle','-','linewidth',1);
hold on
semilogy(iter(k),OBLDE_curve(k),'g-x','linewidth',1);
grid on;
title(['函数收敛曲线',num2str(func_num)])
xlabel('Iterations');
ylabel('Objective function value');
box on
legend('ABC','GA','PSO','SSA','GWO','CSO','DBO','BWO','DE','OBLDE')

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码实现