Gaussian入门学习笔记( 4.输出文件的介绍)

首先打开GaussView画一个水分子，

【之后Calculate下setup，设置一系列后retain，在之后save】具体见之前操作

之后用Gaussian打开，整体设置情况见下图

点击运行

出现Processing Complete说明已经计算完了。点击进行打开

打开后内容如下

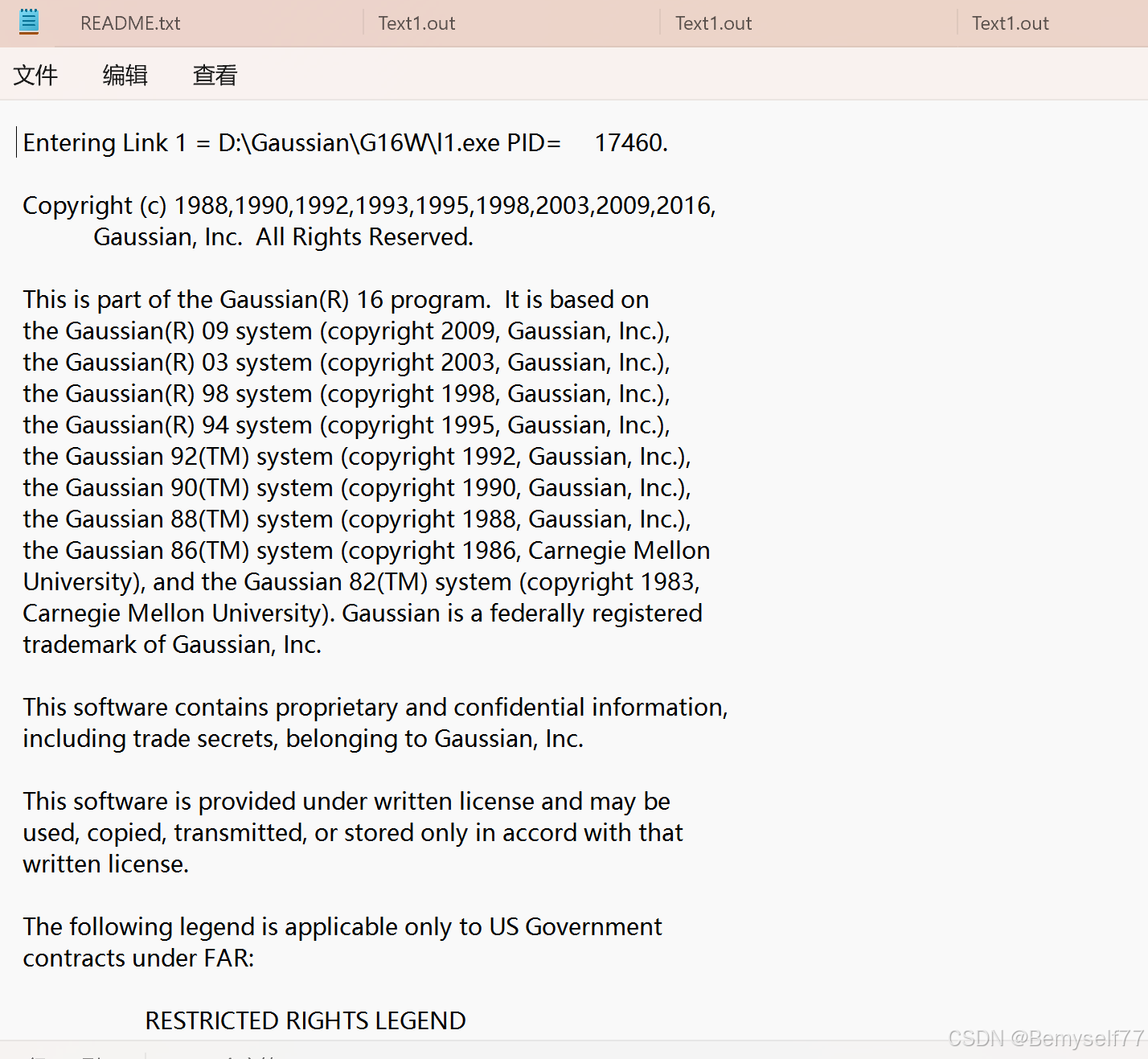
这样的一堆就是通过Gaussian计算得到的，也就是说可以将Gaussian理解为一个模块化的程序，他由很多不同的模块组成，不同模块有不同的功能，可以通过模块来实现数据的计算，这个模块就是link，我们之前在设置中设置了 link0，可以把他理解为 具有初始化程序的控制模块。

整个输出首先是文件和程序的定位，接着往下走是有关于版权的引用

上图下方是使用的软件的版本的信息：Gaussian 16

之后看的出来是将整个输入文件的内容进行了复制，chk文件名，计算路径，非标准执行路径，计算标题名称，电荷自旋多重度，以及坐标。

这一部分记录了 Input orientation（输入取向）部分，原子核间距以及键长

之后是对称性，通过程序判定分子所属点群 

Standard orientation，是程序在计算时，其内部会采用的坐标体系，可用于优化性能，坐标体系的原点是分子的核电荷中心。

standard basis是基组的信息，之后再往下

Intitial guess为初试猜测区， SCF Done为通过单点能计算所得到的能量，注意能量单位是Hartree，1Hartree=2625.5 kj/mol；conv表示自洽场计算，“conv” 用于描述电子密度和能量的迭代计算是否达到收敛标准【自洽场计算是通过不断迭代调整分子轨道和电子密度，直到前后两次迭代的能量变化和轨道系数变化小于某个预设的阈值（收敛标准），此时认为计算达到收敛。】，D-08是10的负8次方。-V/T是维里系数，其中 V 代表势能（Potential Energy），T 代表动能（Kinetic Energy），该数字约等于2，则表明这个计算没有问题

接下来就是布局分析，首先可以看到分子的基态光谱

“Condensed to atoms (all electrons):” 这部分内容 表示的是将电子密度等相关性质按照原子进行凝聚（即把总的电子相关性质分配到各个原子上 ）。

Muliken charges指被估算分子中每一个原子上的总电荷，可以看到氧原子带正电荷，氢原子带负电荷，且整体呈中性

接下来是偶极矩和多极矩，不同于之前的 库仑・米（C・m），单位是德拜（Debye，D），故要进行换算，1D≈3.33564×10−30C⋅m，对于多极矩只有当偶极矩为0时多极矩才算是有用的

接下来是对整块计算的总结不同的内容使用|进行隔开，在这里可以看到光谱项State，总能量HF等

{HF = - 75.9850808：这里的 “HF” 表示 Hartree - Fock 能量，即通过 Hartree - Fock 方法计算得到的体系能量；RMSD = 3.389e - 009：“RMSD” 是均方根偏差（Root - Mean - Square Deviation），在结构优化等计算中，它用于衡量原子坐标的变化程度或收敛情况。数值越小，说明计算结果越稳定，原子坐标的变化越小。Dipole = 0.5774362,0.8170533,0.0：表示分子的偶极矩，通过这些分量可以了解分子在不同方向上的极性特征。Quadrupole = 0.8049899,0.2361295, - 1.0411194, - 0.8032062,0.,0.：表示分子的四极矩，四极矩描述了分子电荷分布的非球形特征，这些数值反映了分子在不同方向上的电荷分布情况。PG = C02V [C2(O1),SGV(H2)]：“PG” 代表点群（Point Group），“C02V” 表示分子的点群对称性，中括号内的内容进一步说明了这种对称性在原子上的体现，类似于之前对框架群的描述，反映了分子的对称特征。}

最后是计算时间和文件大小，最后出现Normal termination出现后就表示计算顺利的结束了