
🌈 个人主页:十二月的猫-CSDN博客
🔥 系列专栏:🏀《PyTorch科研加速指南:即插即用式模块开发》CSDN博客💪🏻 十二月的寒冬阻挡不了春天的脚步,十二点的黑夜遮蔽不住黎明的曙光
目录
1. 前言
- 👑《PyTorch科研加速指南:即插即用式模块开发》专栏持续更新中,未来最少文章数量为60篇。由于专栏刚刚建立,促销价为9.9。后续将慢慢恢复原价至99.9🍉【在校大学生】评论区留言并私信我免费订阅
- 👑《PyTorch科研加速指南:即插即用式模块开发》专栏主要针对零基础入门的小伙伴。不需要Python基础,不需要深度学习基础,只要你愿意学,这一个专栏将真正让你做到零基础入门。
- 🔥每例项目都包括理论讲解、数据集、源代码。
正在更新中💹💹
🚨项目运行环境:
- 平台:Window11
- 语言环境:Python3.8
- 运行环境1:PyCharm 2021.3
- 运行环境2:Jupyter Notebook 7.3.2
- 框架:PyTorch 2.5.1(CUDA11.8)
在这一篇中,我们将掌握PyTorch中Tensor对象的创建和运算方法。Tensor是PyTorch中进行数据存储和运算的基本单元。Tensor之于PyTorch,相当于Array之于NumPy。实际上,PyTorch将NumPy 的Array包装成Tensor,为其定义了各式各样的运算方法和函数,Tensor是Array的为了深度学习而有的升级版。
- Tensor对标Array。
- Tensor相比Array增加了自动求导、反向传播等功能,适用于深度学习。
- Tensor被使用于PyTorch、TensorFlow、MxNet等框架。
- Tensor使用GPU加速计算,Array使用CPU计算。


2. Tensor
Tensor中文叫做 张量,是PyTorch中最基本的数据类型。其与数学中的向量概念有千丝万缕的联系。
2.1 标量、向量、矩阵与张量
数学中有这三个概念:
- 标量:只有大小,没有方向的量。
- 向量:既有大小又有方向的量。如
- 矩阵:由多个向量组成的一堆数字。如
实际上,标量、向量和矩阵都是张量的特例:标量是零维张量、向量是一维张量、矩阵是二维张量。如下图所示,矩阵不过是三维张量下的二维切面。要找到三维张量下的1个标量,我们需要3个维度的坐标。

向量维度:指的是向量中元素数量。如:[3, 5, 7]是一个包含 3 个元素的向量,维度是 3;如:[3, 5]是一个包含 2 个元素的向量,维度是 2。
张量维度:仅仅考虑数据编排形式。数字序列编排则是一维张量(向量),面式编排则是二维张量(矩阵),空间形式编排则是三维张量。
2.2 基本创建方法
在PyTorch中创建张量(以下多称为Tensor)时需要导人torch包,首先在命令行中运行如下命令:
import torch2.2.1 CPU版本
然后使用torch.Tensor()函数创建Tensor。这里我们传入参数(2,4)来构造一个大小为2x4的矩阵x:
x=torch.Tensor(2,4)
x结果如下:

可以看到,这个2×4的矩阵虽然没有初始化,但是已经有了值。
再查看矩阵X类型(张量),输入命令如下:
x.type() #x本身的类型
x.dtype #张量x中数据的类型结果如下:

注意:type是函数;dtype是属性
2.2.2 GPU版本
首先创立torch使用的设备device:
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')然后创建tensor对象:
torch.Tensor(2,3).to(device)结果如下:

输入下面命令,检查其类型为:
gpu_tensor.type()gpu_tensor.dtype结果如下:

2.2.3 Tensor数据类型

例如,我们使用torch.DoubleTensor()函数创建一个2x3x4的64位浮点数Tensor(即y):

从上面的返回值可以看出,变量y的类型是DoubleTensor,即里面每个元素都是64位浮点数。
而且2x3x4的Tensor是由两个3x4的矩阵构成的,符合数学定义。下面对Tensor进行初始化。我们可以通过传入Python原生的List数据结构对其进行初始化:
list = [[1,2,3],[4,5,6],[7,8,9]]
torch.Tensor(list)
然后通过Python的索引方式来获取Tensor中的元素值:
x[0][2]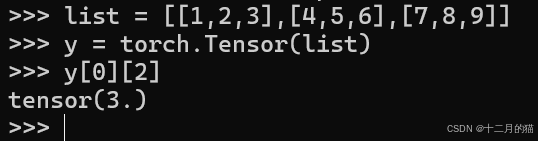
如下图所示,因为在Tensor中索引l从0开始计算,所以x[0][2]表示第1行第3列的元素;又因为其默认类型是torch.FloatTensor,所以返回值为tensor(5.)。

我们可以通过索引修改Tensor中的元素:

2.3 快速创建方法
下面介绍几个快速创建Tensor的方法:
2.3.1 torch.zero()
用于创建元素全为0的Tensor:

2.3.2 torch.eye()
用于创建主对角线位置元素全为1,其他位置为0的Tensor:

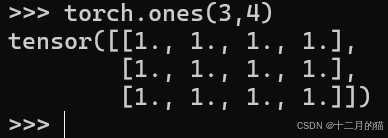
2.3.3 torch.ones()
用于创建元素全为1的Tensor:
2.3.4 torch.rand()
用于创建将元素初始化为区间[0,1)的随机数的Tensor:

2.3.5 torch.arange()
用于创建一个在区间内按指定步长递增的一维Tensor,前两个参数指定区间范围,第三个参数指定步长(默认为1):

2.3.6 torch.linspace()
用于创建一个区间,前两个参数指定区间范围。并将区间划为n块,n由第三个参数决定。

常见快速创建Tensor方法如下:

2.4 Tensor常用数学操作
在PyTorch官方文档上,Tensor的数学操作方法有90多种,比较常用的有25种数学操作方法。


Tensor的数学操作的实现方法一般有两种:第一种是直接用Tensor实例调用数学操作方法,第二种是使用torch库的方法。
2.4.1 加法操作
比如在进行加法操作前,先初始化两个形状相同的Tensor,因为形状不同的Tensor无法直接相加。本例中,初始化两个形状为2x3的Tensor(即a和b):

使用第一种方法:Tensor实例调用数学操作方法。

使用第二种方法:调用torch库函数。

特别地,如果数学操作函数带有下划线,返回值将覆盖对象,如下图中a+b覆盖了b:
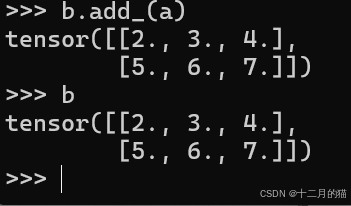
数学运算中的广播机制。允许一个张量Tensor中的每个元素加上同一个标量,如:

2.4.2 另外四种常见的数学操作
abs():返回Tensor中每个元素的绝对值(类函数、库函数)

ceil():对Tensor中的每个元素向上取整(类函数、库函数)

exp():返回Tensor中每个元素的以e为底的指数

max():返回Tensor中所有元素的最大值

2.5 线性代数运算
除了基本的数学操作外,torch包中还包含了约12种线性代数的相关函数。接下来,我们简单介绍一下其中的3种运算。
2.5.1 使用torch.dot()实现内积

假如你已经忘记了或者没有学过点积,请别担心,现在就让我们重新温习一遍。向量的点积
定义起来很简单。假设有两个向量a=[a,a2,... ,an],b=[b,b2,…,bn],那么a与b的点
积定义为:
从定义上可以发现,两个向量进行点积,得到的结果是一个标量。将上面代码中张量a和张量b的值代入a与b中,我们可以使用点积定义的公式进行推导:
2.5.2 使用torch.mv()实现矩阵与向量的乘法

矩阵与向量的乘法规则如下所示:
根据上面的代码,我们可以还原成以下数学表达:
答案与上面相同🥰🥰~~~
2.5.3 使用torch.mm()将两个矩阵相乘

矩阵与矩阵的乘法定义如下:
其中。根据上述代码,我们可以还原上述数学表达:
其他线性代数操作方法:

import torch # 创建两个批量张量 input = torch.randn(10, 3, 5) # (b=10, n=3, m=5) mat2 = torch.randn(10, 5, 2) # (b=10, m=5, p=2) # 使用 bmm 进行批量矩阵乘法 output = torch.bmm(input, mat2) # 输出的形状为 (b=10, n=3, p=2) print(output.shape) # 输出: torch.Size([10, 3, 2])
input张量的形状为(10, 3, 5),表示批次大小为 10,每个矩阵是 3x5。mat2张量的形状为(10, 5, 2),表示批次大小为 10,每个矩阵是 5x2。- 结果
output张量的形状为(10, 3, 2),表示每对矩阵乘积的结果是一个 3x2 的矩阵。
2.6 连接和切片
2.6.1 torch.cat实现连接
首先介绍如何使用torch.cat()函数将多个Tensor沿某维度进行连接。我们使用rand()函数随机初始化两个形状为2x2的Tensor:

cat()函数需要传人两个参数:第一个参数是由需要进行连接的所有Tensor组成的元组;第二个参数是连接的维度。如果让a按照第一个维度(行)与b进行连接,则传人的第二个参数为0:

如果让a按照第二个维度(列)与b进行连接,则传人的第二个参数为1:

2.6.2 切片
接下来介绍如何使用torch.chunk()函数将Tensor沿某维度进行切片。我们先初始化一个Tensor实例a:

再用torch.chunk()函数进行切片。chunk()函数需要传入3个参数:第一个参数为被切片的Tensor对象,第二个参数为切分的块数,第三个参数为切分的维度。下面我们将张量c按第二个维度切分为两块:

2.6.3 矩阵转置
最后介绍如何使用torch.t()函数来转置矩阵。注意,该函数只适用于二维的Tensor(即矩阵):

常见的连接和切片操作:

2.7 变形
view()函数可以改变Tensor的形状。在深度神经网络的卷积层与全连接层中,我们时常将高维的Tensor转化为一维的Tensor,这个过程就是使用view()函数完成的。下面举个简单的例子,我们先随机初始化一个2x3x4的Tensor:

接着,使用view()函数将这个Tensor转化成一个2x12的Tensor,总元素的数目保持不变:

当使用-1作为view()函数的参数时,代表该维度数目自动计算。下面的代码表示我们确定第二维为1,第一维自动计算。运行代码后,会得到一个24x1的Tensor:

3. CUDA加速
在深度学习的训练过程中,经常需要庞大的计算量。用CPU进行数值计算的时间周期较长,难以立即得到计算结果。因此,在实际的深度学习训练过程中,我们通常会利用GPU进行加速运算。使用GPU进行加速计算之前,先运行下面的代码查看计算机是否支持CUDA加速:
torch.cuda.is_available()如果返回True,那么恭喜你,你可以直接使用GPU进行加速计算。如果返回False,则可能有两种情况:第一种是计算机没有支持CUDA的NVIDIA显卡,第二种是显卡驱动、CUDA或cuDNN等软件没有成功安装。
如果确认自己电脑有NVIDIA显卡,但是仍然没有CUDA可以看另一篇文章:【一篇搞定配置】小白如何安装/配置/删除CUDA(详细图文)-CSDN博客
为了对比CPU和GPU计算速度的差距,我们以一个1000×10000的矩阵与10000×10000的矩阵进行相乘为例,分别使用CPU和GPU进行计算,对比两者花费的时间。
首先导入time库中的clock()函数用于计时:

下面我们使用cuda()函数。矩阵x和Y接下来进行的任何运算都会调用GPU进行加速计算:
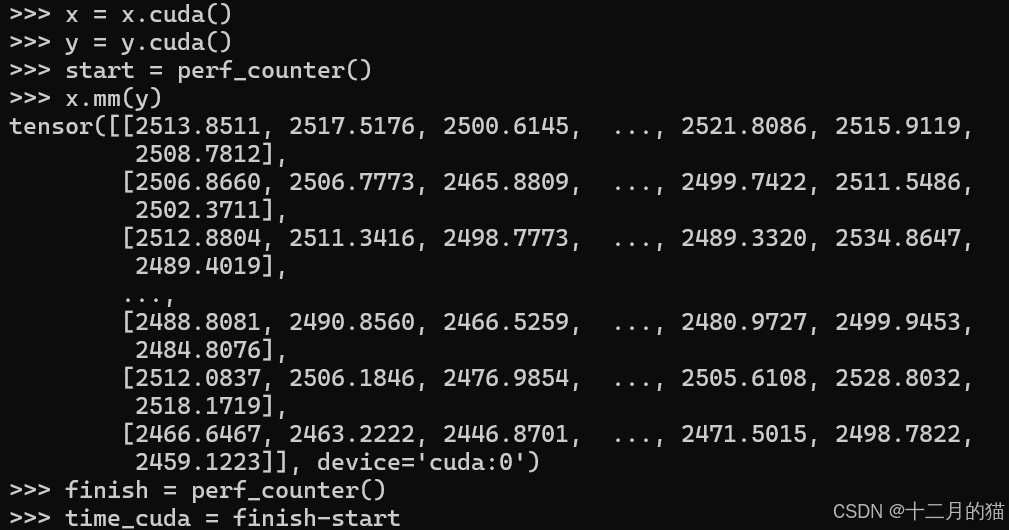
GPU和CPU在矩阵乘法上的差距:

因此,GPU在矩阵数值运算的速度远超过CPU。
4. 总结
【如果想学习更多深度学习文章,可以订阅一下热门专栏】
如果想要学习更多pyTorch/python编程的知识,大家可以点个关注并订阅,持续学习、天天进步你的点赞就是我更新的动力,如果觉得对你有帮助,辛苦友友点个赞,收个藏呀~~~


























 1321
1321

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










