1.SPWM采用三相正弦波调制,在调制度为1时,输出相电压的基波幅值为什么为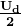 ?
?

如图为交-直-交PWM变频器主回路结构,左边为不可控整流桥,将三相交流电整流成电压恒定的直流电压,右边是逆变器,将直流电压变换为频率与电压均可调的交流电,中间的滤波环节是为了较小直流电压脉动而设置的。
正弦波脉宽调制(SPWM)技术
以频率与期望的输出电压波相同的正弦波作为调制波,以频率比期望高的多的等腰三角波作为载波,当调制波与载波相交时,由它们的交点确定逆变器开关器件的通断时刻,从而获得幅值相等、宽度按正弦规律变化的脉冲序列,这种调制方法称作正弦波脉宽调制(SPWM)。


这组图像很重要,能够帮助我们理清楚它们之间的关系。
当调制深度为1,即,也就是载波幅值与调制波幅值相等,从电源电压最大利用率的角度来说,载波幅值和调制波幅值都为
,图(bcd)是逆变器输出脉冲波形,图(f)是电动机相电压波形,通过平均值等效原理,就可以合成图(a)的调制波,即最后施加给电机的等效正弦电压。而其基波幅值就为
.补充:其实图(bcd)和图(f)合成的调制波形是一样的,那为何它们两者之间的波形不一样呢,这是因为参考点不同导致的。
这里插入一个题外话,就是线电压和相电压之间的关系
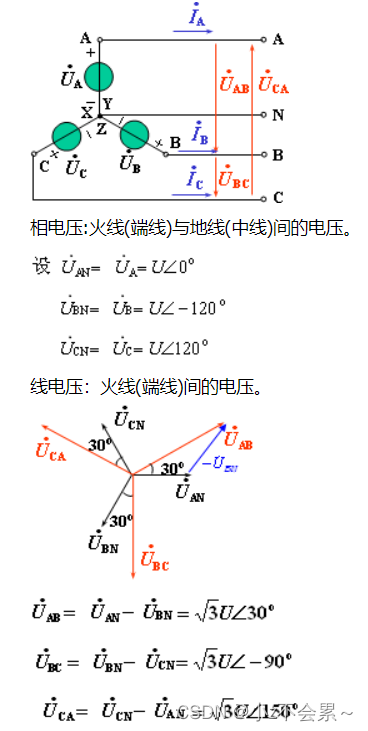
观察这幅图,相电压如是两个相电压的合成,而幅值关系就是
的倍数关系。
结论
SPWM采用三相正弦波调制,在调制度为1时,输出相电压的基波幅值为,输出线电压的基波幅值为
,直流电压的利用率仅为
。若调制深度大于1,直流电压的利用率可以提高,但会产生失真现象,谐波分量增加。采用电压空间矢量PWM调制(SVPWM)或三次谐波注入法,可有效提高直流电压的利用率。
2.为何SVPWM输出相电压幅值的基波幅值最大为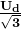 ?
?
电压空间矢量PWM(SVPWM)控制技术(磁链跟踪控制技术)
经典的SPWM控制主要着眼于使变压变频器的输出电压尽量接近正弦波,并未顾及输出电流的波形。而电流跟踪控制则直接控制输出电流,使之在正弦波附近变化,这就比只要求正弦电压前进了一步。然而交流电动机需要输入三相正弦电流的最终目的是在电动机空间形成圆形旋转磁场,从而产生恒定的电磁转矩。把逆变器和交流电动机视为一体,以圆形旋转磁场为目标来控制逆变器工作,这种控制方法称作“磁链跟踪控制”,磁链轨迹的控制是通过交替使用不同的电压空间矢量实现的,所以又称“电压控制矢量PWM控制”。



是一个以电源角频率
为角速度做恒速旋转的空间矢量,它的幅值是相电压幅值的
倍,当某一相电压为最大值时,合成电压矢量
就落在该相的轴线上。在三相平衡正弦电压供电时,若电动机转速已稳定,则定子电流和磁链的控制矢量
和
的幅值恒定,以电源角频率
为电气角速度在空间做恒速旋转。
这里为何合成矢量是定子相电压的倍呢?但是有的书中合成矢量是定子相电压的
倍呢?袁雷的《永磁同步电机控制原理》里面推导的是定子相电压的
倍
其实这是针对从不同角度来说的,恒功率原则针对的是电压的有效值,即推导出的是定子相电压的倍,而袁雷书中,是从瞬时值的角度来说的,所以推导出的是定子相电压的
倍。
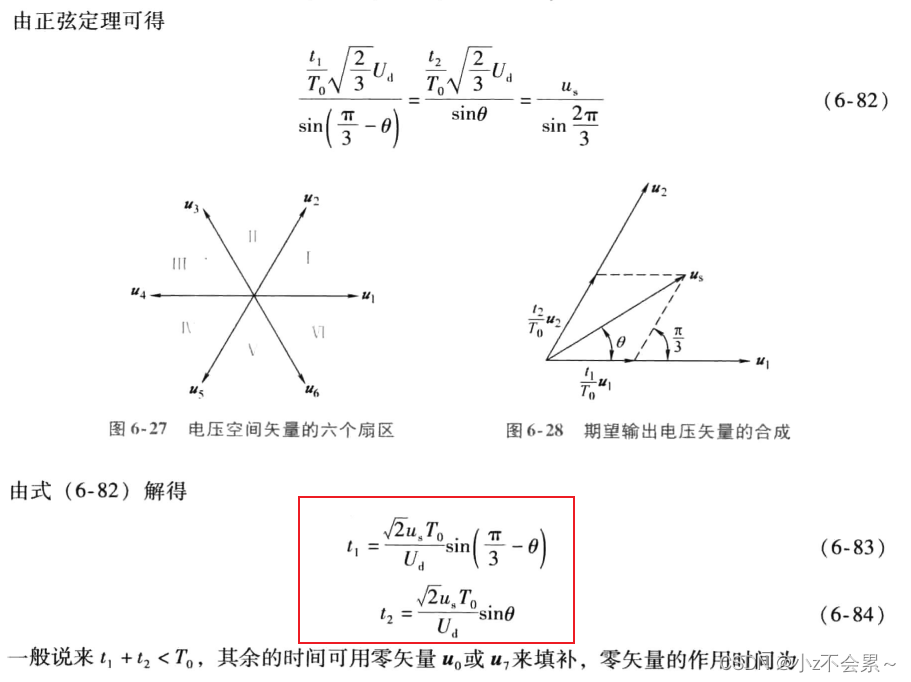
这里继续插入一个题外话,探讨一下最终合成的矢量的大小,从瞬时值角度考虑

六个非零矢量的大小为,而三相相位相差120°的相电压合成的空间矢量
的幅值是相电压幅值的
倍,所以
的瞬时最大幅值为
。
从恒功率角度考虑,即电压有效值
相电压最大幅值为,而基波幅值为
,经过恒功率计算,三相电压合成的电压矢量大小是其幅值的
倍,所以计算得到
的最大幅值为
。这里其实是均值合成后的有效电压。
这样就联系起来了,合成矢量其实是以
为幅值的正弦波,其有效电压值最大为
,而瞬时最大值为
。





总结
简单来说可以理解为,当调制深度最大即为1时,SPWM算法能够完成相电压幅值为三相电压复现从而施加给电动机,而SVPWM算法能够完成相电压幅值为
三相电压的复现,所以电压利用率之比为(或者说提高了调制深度)
。
3.继续探讨SPWM和SVPWM的区别
SPWM在每一个扇区内,只使用一个电压矢量去产生磁链从而拉动电机旋转,最后形成的是一个正六边形磁链轨迹。




4.将算法与我们常用的电机控制相结合
直流无刷(BLDC)电机控制,通常采用六步换相控制,也就是SPWM算法。而永磁同步电机(PMSM)采用的是矢量控制,即SVPWM算法。
表面上,BLDC和PMSM的基本结构是相同的,共同点如下:
1、他们本质上都是永磁电动机,转子由永磁体组成基本结构,定子安放有多相交流绕组;
2、都是由永磁体转子和绕组定子的交流电流相互作用产生电机的转矩,本质利用的物理原理都是通电导体在磁场中受力;
3、在绕组中的驱动电流必须与转子位置反馈同步;
不同点如下:
1.直流无刷电机BLDC是方波电流驱动,而永磁同步电动机PMSM是正弦波电流驱动,这是主要的不同之处,但是他们的调制波均是三相正弦电压。
2.永磁同步电机PMSM在电气和机械方面更加安静,转矩基本没有脉动,而BLDC是方波驱动,存在转矩脉动。其原因在于:由于电感存在, 电流不会突变,因此在换相过程中断开相电流,电流下降的过程和新接入的新相电流上升过程都需要时间,因此相电流不可能是理想的方波,从而会产生非换相相电流脉动,从而引起换相转矩脉动。
3、因为驱动电流不同,气隙磁场波形、反电动势波形、转矩波形均不相同。BLDC反电动势波形为梯形波,PMSM反电动势波形为正弦波。
4、电流环路结构不同,速度反馈信息的获取也不相同。
5、电动机气息磁通密度分布设计和绕组设计不同,一个是针对正弦波驱动,一个是针对方波驱动,永磁同步电机追求正弦磁通,其绕组分布更多更分散,而无刷直流电机相对简单,所以无刷直流电机造价相对便宜一些。
从仿真的角度进行验证SPWM和SVPWM三相驱动电流的区别,对象为永磁同步电机
搭建仿真,观察SPWM算法下,电机的三相驱动电流

仿真结果
波形如下:

可以观察到其驱动电流为近似梯形波
搭建仿真,观察SVPWM算法下,电机的三相驱动电流
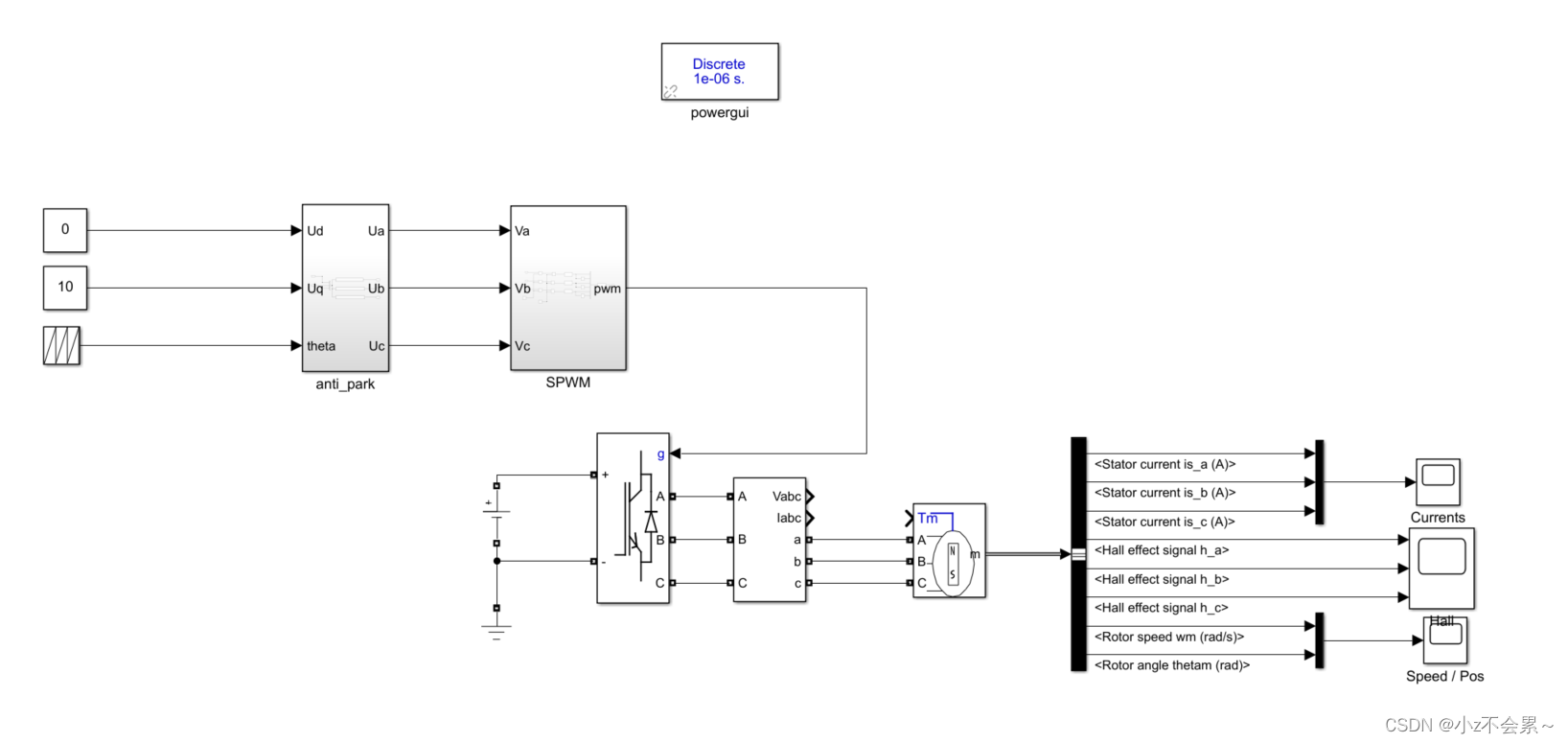
仿真结果
波形如下:

可以观察到其驱动电流为近似正弦波
接下来搭建仿真验证BLDC的反电势波形
思路:
1.选定BLDC电机仿真模型;
2.保持BLDC电机三相开路;
3.施加外力让电机旋转;
4.测量反电势波形;

求解器参数设置

BLDC电机参数设置
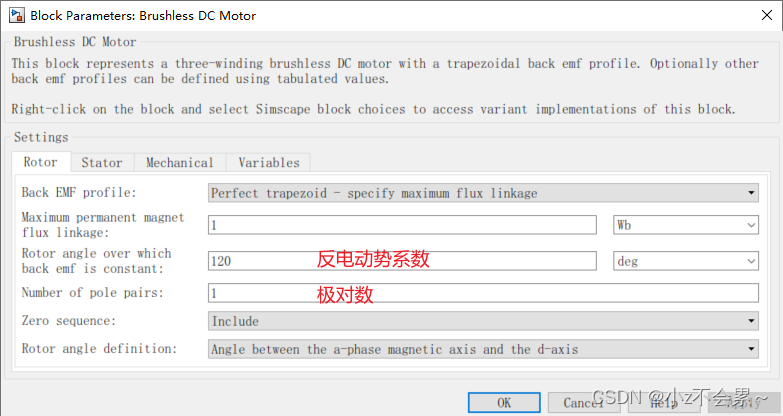

仿真结果

观察仿真结果,我们可以发现其反电势波形为梯形波
本文中关于SPWM和SVPWM算法的详细推导摘自《电力拖动自动控制系统》,感谢大家的阅读!!^_^























 4527
4527

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








