✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
“板凳龙”,又称“盘龙”,是浙闽地区的传统地方民俗文化活动。人们将少则几十条, 多则上百条的板凳首尾相连,形成蜿蜒曲折的板凳龙。盘龙时,龙头在前领头,龙身和龙尾相随盘旋,整体呈圆盘状。一般来说,在舞龙队能够自如地盘入和盘出的前提下,盘龙所需要的面积越小、行进速度越快,则观赏性越好。
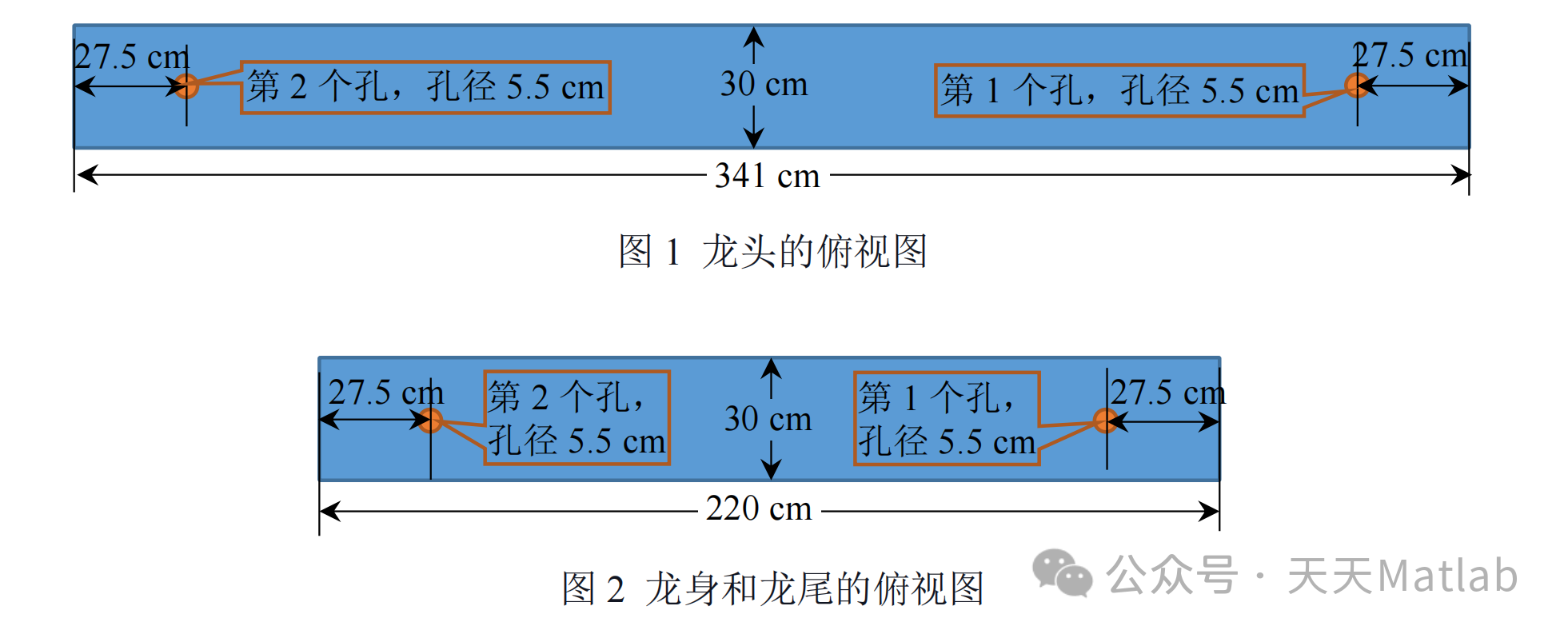
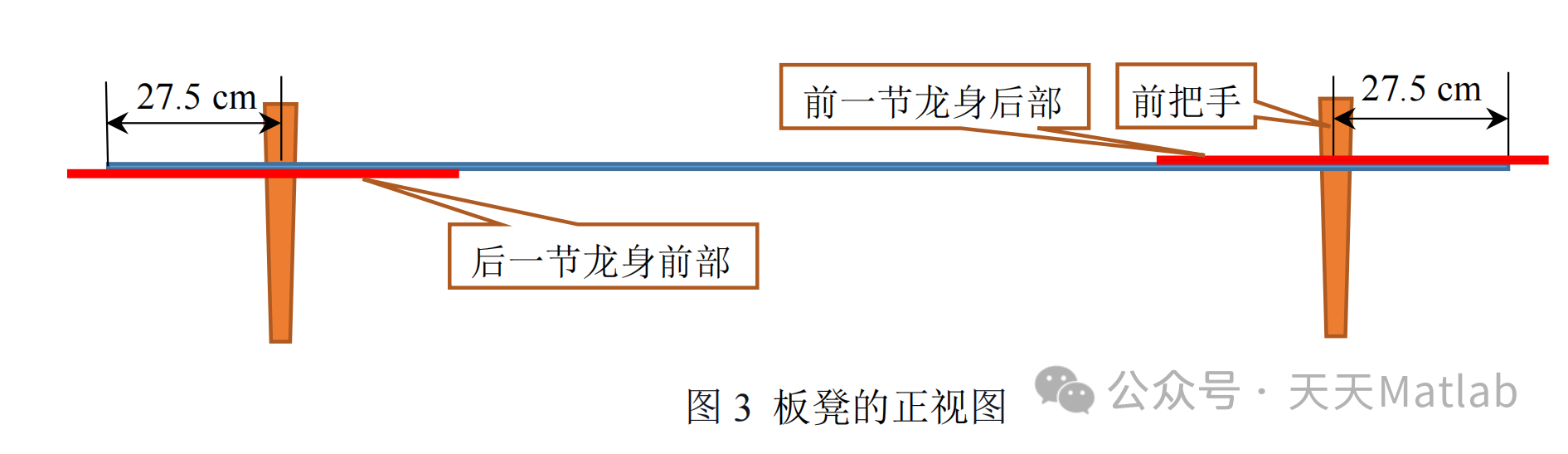
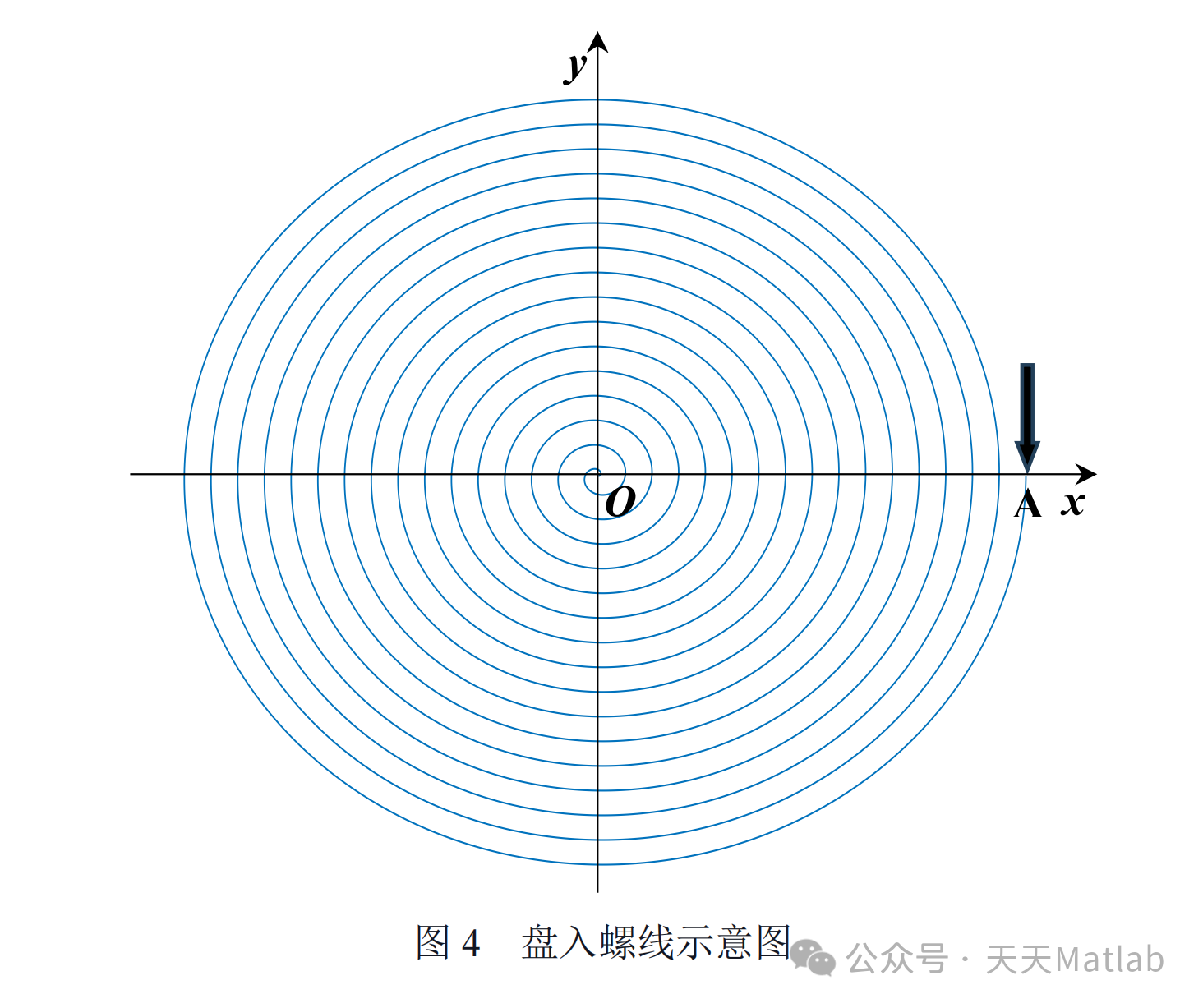
某板凳龙由 223 节板凳组成,其中第 1 节为龙头,后面 221 节为龙身,最后 1 节为龙尾。龙头的板长为 341 cm,龙身和龙尾的板长均为 220 cm,所有板凳的板宽均为 30 cm。每节板凳上均有两个孔,孔径(孔的直径)为 5.5 cm,孔的中心距离最近的板头 27.5 cm(见图 1 和图 2)。相邻两条板凳通过把手连接(见图 3)。
问题 1 舞龙队沿螺距为 55 cm 的等距螺线顺时针盘入,各把手中心均位于螺线上。龙头前把手的行进速度始终保持 1 m/s。初始时,龙头位于螺线第 16 圈 A 点处(见图 4)。请给出从初始时刻到 300 s 为止,每秒整个舞龙队的位置和速度(指龙头、龙身和龙尾各前把手及龙尾后把手中心的位置和速度,下同),将结果保存到文件 result1.xlsx 中(模板文件见附件,其中“龙尾(后)”表示龙尾后把手,其余的均是前把手,结果保留 6 位小数,下同)。
同时在论文中给出 0 s、60 s、120 s、180 s、240 s、300 s 时,龙头前把手、龙头后面第 1、51、101、151、201 节龙身前把手和龙尾后把手的位置和速度(格式见表 1 和表 2)。

📣 赛题分析
难度: 中等偏上 适合专业: 工程力学、机械工程、物理、计算机科学、数学等专业的学生适合解答这一题。特别是有扎实几何建模、力学和动态模拟基础的同学 主要算法和模型: 1. 几何建模: 需要建立空间几何模型,可以用螺旋线方程、空间曲线运动方程来描述舞龙队的位置和速度。2. 动力学模拟: 可以使用微分方程或刚体动力学模拟工具。3. 数值计算与优化: 涉及优化空间,可能需要优化算法(如线性规划、非线性优化)。4. 仿真软件: MATLAB或Python等编程工具中的物理引擎或自定义仿真模块会是主要的工具
2. 坐标系建立与模型假设
为了方便分析,我们将板凳龙的运动轨迹投影到水平面上,建立以龙头初始位置 A 为原点,指向龙头运动方向为 x 轴正方向,垂直于 x 轴指向纸面外为 y 轴正方向的直角坐标系。
为了简化模型,我们做以下假设:
-
每个板凳视为一个质点,其质量集中于把手中心。
-
板凳之间连接的把手不可伸缩,且连接处无摩擦力。
-
板凳龙的运动轨迹为完美的等距螺线,且螺线始终保持水平。
-
龙头前把手的速度始终保持 1 m/s,且方向始终沿着螺线切线方向。
3. 数学模型
根据等距螺线的数学性质,我们可以得到以下公式:


通过对板凳龙盘入运动轨迹的分析,我们发现:
-
龙头前把手的速度始终保持 1 m/s,而其他把手由于连接关系,速度会随着时间推移逐渐增加。
-
由于螺线曲率的变化,龙身各把手的位置和速度会逐渐发生变化,呈现出螺旋状的运动轨迹。
-
由于螺线曲率的变化,龙身各把手的速度方向会随着时间推移逐渐偏离 x 轴正方向,逐渐趋向于螺线切线方向。
🔗 参考代码
























 2890
2890

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










