根轨迹法的基本概率(*)
基本概率
根轨迹法:
三大分析校正方法之一
根轨迹:
系统某一参数由 0 → ∞ 0\rightarrow\infty 0→∞变化时, λ \lambda λ在 s s s平面相应变化所描绘出来的轨迹
根轨迹法的特点:
- 图解方法,直观、形象
- 适合于研究当系统某一参数变化时,系统性能的变化趋势
- 近似方法,不十分精确
例1 系统结构图如图所示,分析 λ \lambda λ随开环增益 K K K变化的趋势

G
(
s
)
=
K
s
(
0.5
s
+
1
)
=
K
∗
=
2
K
s
(
s
+
2
)
{
K
:
开环增益
K
∗
:
根轨迹增益
Φ
(
s
)
=
G
(
s
)
1
+
G
(
s
)
=
K
∗
s
2
+
2
s
+
K
∗
D
(
s
)
=
s
2
+
2
s
+
K
∗
=
0
λ
1
,
2
=
−
1
±
1
−
K
∗
\begin{aligned} G(s)&=\frac{K}{s(0.5s+1)}=\frac{K^*=2K}{s(s+2)}\\ &\begin{cases}K:\quad开环增益\\K^*:\quad根轨迹增益\end{cases}\\ \Phi(s)&=\frac{G(s)}{1+G(s)}=\frac{K^*}{s^2+2s+K^*}\\ D(s)&=s^2+2s+K^*=0\\ \lambda_{1,2}&=-1\pm\sqrt{1-K^*}\\ \end{aligned}
G(s)Φ(s)D(s)λ1,2=s(0.5s+1)K=s(s+2)K∗=2K{K:开环增益K∗:根轨迹增益=1+G(s)G(s)=s2+2s+K∗K∗=s2+2s+K∗=0=−1±1−K∗



- 根据根轨迹,可以大致对系统的动态性能和稳定性做出判断
- 开环传递函数为首1标准型时,对应的系数 K ∗ K^* K∗为根轨迹增益(没有闭环的根轨迹增益)
根轨迹方程及其含义

G
(
s
)
=
K
∗
s
−
p
Φ
(
s
)
=
G
(
s
)
1
+
G
(
s
)
D
(
s
)
=
1
+
G
(
s
)
=
0
G
(
s
)
=
−
1
,
根轨迹方程
{
∣
G
(
s
)
∣
=
K
∗
∣
s
−
p
∣
=
1
∠
G
(
s
)
=
−
∠
(
s
−
p
)
=
(
2
k
+
1
)
π
\begin{aligned} G(s)&=\frac{K^*}{s-p}\\ \Phi(s)&=\frac{G(s)}{1+G(s)}\\ D(s)&=1+G(s)=0\\ G(s)&=-1,\quad根轨迹方程\\ &\begin{cases}|G(s)|=\frac{K^*}{|s-p|}=1\\\angle G(s)=-\angle(s-p)=(2k+1)\pi\\\end{cases} \end{aligned}
G(s)Φ(s)D(s)G(s)=s−pK∗=1+G(s)G(s)=1+G(s)=0=−1,根轨迹方程{∣G(s)∣=∣s−p∣K∗=1∠G(s)=−∠(s−p)=(2k+1)π
一般情况下
G
(
s
)
H
(
s
)
=
K
∗
(
s
−
z
1
)
.
.
.
(
s
−
z
m
)
(
s
−
p
1
)
(
s
−
p
2
)
.
.
.
(
s
−
p
n
)
=
K
∗
∏
i
=
1
m
(
s
−
z
i
)
∏
j
=
1
n
(
s
−
p
j
)
Φ
(
s
)
=
G
(
s
)
1
+
G
(
s
)
H
(
s
)
G
(
s
)
H
(
s
)
=
K
∗
(
s
−
z
1
)
.
.
.
(
s
−
z
m
)
(
s
−
p
1
)
(
s
−
p
2
)
.
.
.
(
s
−
p
n
)
=
−
1
,
根轨迹方程
∣
G
(
s
)
H
(
s
)
∣
=
K
∗
∣
s
−
z
1
∣
.
.
.
∣
s
−
z
m
∣
∣
s
−
p
1
∣
∣
s
−
p
2
∣
.
.
.
∣
s
−
p
n
∣
=
K
∗
∏
i
=
1
m
∣
s
−
z
i
∣
∏
j
=
1
n
∣
s
−
p
j
∣
=
1
模值条件
∠
G
(
s
)
H
(
s
)
=
∑
i
=
1
m
∠
(
s
−
z
i
)
−
∑
j
=
1
n
∠
(
s
−
p
i
)
=
(
2
k
+
1
)
π
相角条件
\begin{aligned} G(s)H(s)&=\frac{K^*(s-z_1)...(s-z_m)}{(s-p_1)(s-p_2)...(s-p_n)}=\frac{K^*\prod_{i=1}^m(s-z_i)}{\prod_{j=1}^n(s-p_j)}\\ \Phi(s)&=\frac{G(s)}{1+G(s)H(s)}\\ G(s)H(s)&=\frac{K^*(s-z_1)...(s-z_m)}{(s-p_1)(s-p_2)...(s-p_n)}=-1,\quad根轨迹方程\\ |G(s)H(s)|&=\frac{K^*|s-z_1|...|s-z_m|}{|s-p_1||s-p_2|...|s-p_n|}=\frac{K^*\prod_{i=1}^m|s-z_i|}{\prod_{j=1}^n|s-p_j|}=1\quad模值条件\\ \angle G(s)H(s)&=\sum_{i=1}^m\angle(s-z_i)-\sum_{j=1}^n\angle(s-p_i)=(2k+1)\pi\quad相角条件\\ \end{aligned}
G(s)H(s)Φ(s)G(s)H(s)∣G(s)H(s)∣∠G(s)H(s)=(s−p1)(s−p2)...(s−pn)K∗(s−z1)...(s−zm)=∏j=1n(s−pj)K∗∏i=1m(s−zi)=1+G(s)H(s)G(s)=(s−p1)(s−p2)...(s−pn)K∗(s−z1)...(s−zm)=−1,根轨迹方程=∣s−p1∣∣s−p2∣...∣s−pn∣K∗∣s−z1∣...∣s−zm∣=∏j=1n∣s−pj∣K∗∏i=1m∣s−zi∣=1模值条件=i=1∑m∠(s−zi)−j=1∑n∠(s−pi)=(2k+1)π相角条件
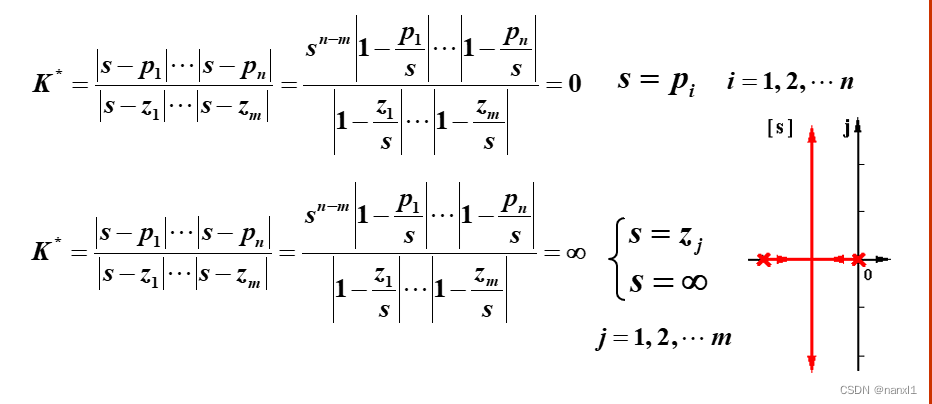
例2 判定 s i s_i si是否为根轨迹上的点
G ( s ) = K ∗ ( s + 1 ) ( s + 5 ) 根轨迹方程 : G ( s ) = − 1 模值条件 : K ∗ = ∣ s + 1 ∣ ∣ s + 5 ∣ 相角条件 : − ∠ ( s − p 1 ) − ∠ ( s − p 2 ) = ( 2 k + 1 ) π Δ 1 = − 2 { K Δ 1 ∗ = ∣ − 2 + 1 ∣ ∣ − 2 + 5 ∣ = 3 √ − ∠ ( − 2 + 1 ) − ∠ ( − 2 + 5 ) = − 180 − 0 = − 180 √ Δ 2 = − 8 { K Δ 2 ∗ = ∣ − 8 + 1 ∣ ∣ − 8 + 5 ∣ = 21 √ − ∠ ( − 8 + 1 ) − ∠ ( − 8 + 5 ) = − 360 × Δ 3 = − 7 + j 4 { K Δ 3 ∗ = ∣ − 7 + j 4 + 1 ∣ ∣ − 7 + j 4 + 5 ∣ = 32.25 √ − ∠ ( − 7 + j 4 + 1 ) − ∠ ( − 7 + 4 j + 5 ) ≠ ( 2 k + 1 ) π × Δ 4 = − 3 + j 3 { K Δ 4 ∗ = ∣ − 3 + j 3 + 1 ∣ ∣ − 3 + j 3 + 5 ∣ = 13 √ − ∠ ( − 3 + j 3 + 1 ) − ∠ ( − 3 + j 3 + 5 ) = − 180 √ \begin{aligned} G(s)&=\frac{K*}{(s+1)(s+5)}\\ 根轨迹方程:\quad&G(s)=-1\\ 模值条件:&\quad K^*=|s+1||s+5|\\ 相角条件:&\quad-\angle{(s-p_1)}-\angle{(s-p_2)}=(2k+1)\pi\\ \Delta_1&=-2\quad\begin{cases}K^*_{\Delta_1}=|-2+1||-2+5|=3\quad\surd\\-\angle{(-2+1)}-\angle{(-2+5)=-180-0=-180}\quad\surd\end{cases}\\ \Delta_2&=-8\quad\begin{cases}K^*_{\Delta_2}=|-8+1||-8+5|=21\quad\surd\\-\angle{(-8+1)-\angle{(-8+5)=-360}\quad\times}\end{cases}\\ \Delta_3&=-7+j4\quad\begin{cases}K^*_{\Delta_3}=|-7+j4+1||-7+j4+5|=32.25\quad\surd\\-\angle{(-7+_j4+1)}-\angle{(-7+4j+5)\neq(2k+1)\pi}\quad\times\end{cases}\\ \Delta_4&=-3+j3\quad\begin{cases}K^*_{\Delta_4}=|-3+j3+1||-3+j3+5|=13\quad\surd\\-\angle{(-3+j3+1)-\angle{(-3+j3+5)}}=-180\quad\surd\end{cases} \end{aligned} G(s)根轨迹方程:模值条件:相角条件:Δ1Δ2Δ3Δ4=(s+1)(s+5)K∗G(s)=−1K∗=∣s+1∣∣s+5∣−∠(s−p1)−∠(s−p2)=(2k+1)π=−2{KΔ1∗=∣−2+1∣∣−2+5∣=3√−∠(−2+1)−∠(−2+5)=−180−0=−180√=−8{KΔ2∗=∣−8+1∣∣−8+5∣=21√−∠(−8+1)−∠(−8+5)=−360×=−7+j4{KΔ3∗=∣−7+j4+1∣∣−7+j4+5∣=32.25√−∠(−7+j4+1)−∠(−7+4j+5)=(2k+1)π×=−3+j3{KΔ4∗=∣−3+j3+1∣∣−3+j3+5∣=13√−∠(−3+j3+1)−∠(−3+j3+5)=−180√

- 对 s s s平面上任意的点,总存在一个 K ∗ K^* K∗,使其满足模值条件,但该点不一定是根轨迹上的点
- s s s平面上满足相角条件的点(必定满足模值条件)一定在根轨迹上
- 满足相角条件是 s s s点位于根轨迹上的充分必要条件
- 根轨迹上某点对应的 K ∗ K^* K∗值,应由模值条件确定
绘制根轨迹的基本法则(重点)
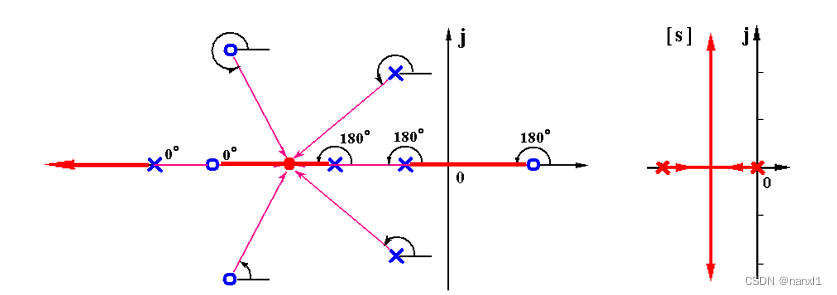
法则1: 根轨迹的起点和终点
根轨迹起始于开环极点,终止于开环零点;如果开环极点的个数n大于开环零点个数m,则有n-m条根轨迹终止于无穷处
法则2: 根轨迹的分支数,对称性和连续性
根轨迹的分支数=开环极点数;根轨迹连续且对称于实轴
- 根轨迹对称于实轴,是因为根轨迹方程的解要么是单根要么是共轭的复数
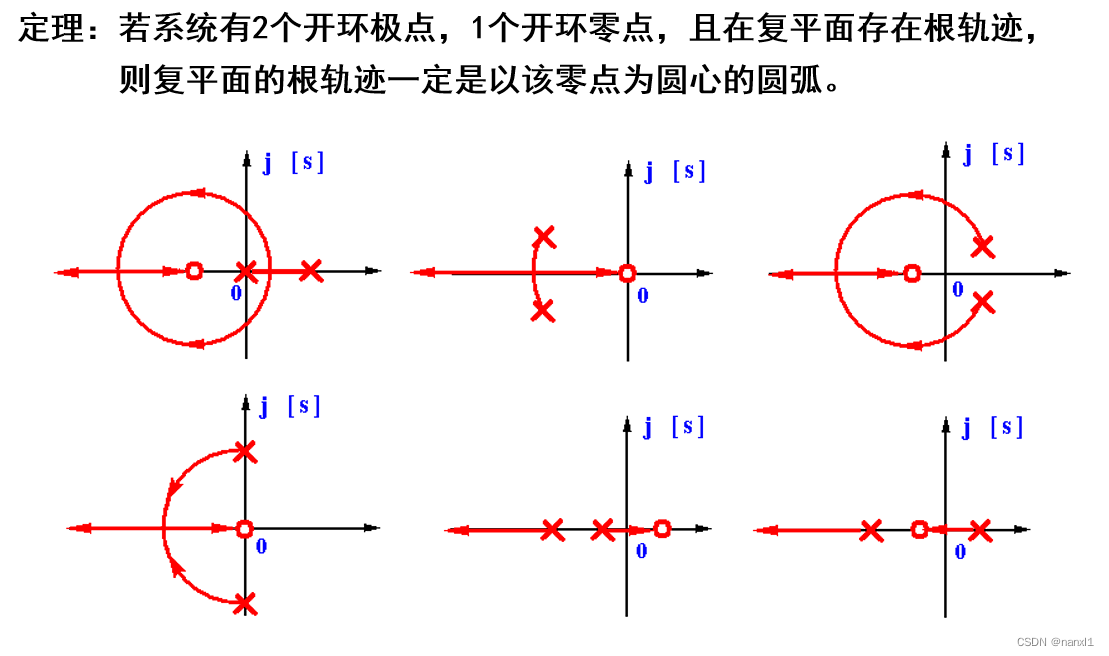
法则3: 实轴上的根轨迹:
从实轴上最右端的开环零、极点算起,奇数开环零、极点到偶数开环零、极点之间的区域必是根轨迹。
根轨迹的相角关系由极点和零点共同决定
本质上是满足了相角条件
∠
G
(
s
)
H
(
s
)
=
∑
i
=
1
m
∠
(
s
−
z
i
)
−
∑
j
=
1
n
∠
(
s
−
p
i
)
=
(
2
k
+
1
)
π
相角条件
\angle G(s)H(s)=\sum_{i=1}^m\angle(s-z_i)-\sum_{j=1}^n\angle(s-p_i)=(2k+1)\pi\quad相角条件\\
∠G(s)H(s)=i=1∑m∠(s−zi)−j=1∑n∠(s−pi)=(2k+1)π相角条件
法则4: 根之和: ∑ i = 1 n λ i = C ( n − m ≥ 2 ) \sum_{i=1}^n\lambda_i=C(n-m\ge2) ∑i=1nλi=C(n−m≥2)
n − m ≥ 2 n-m\ge2 n−m≥2时,闭环根之和保持一个常值

例题
例3


两个开环极点一个开环零点的常见根轨迹
法则5: 渐进线: { σ a = ∑ i = 1 n p i − ∑ j = 1 m z i n − m φ a = ( 2 k + 1 ) π n − m \begin{cases}\sigma_a=\frac{\sum_{i=1}^np_i-\sum_{j=1}^mz_i}{n-m}\\\varphi_a=\frac{(2k+1)\pi}{n-m}\end{cases} {σa=n−m∑i=1npi−∑j=1mziφa=n−m(2k+1)π
-
n>m时,n-m条根轨迹趋近于无穷远处的规律
-
σ a \sigma_a σa是渐近线与实轴的交点( σ a \sigma_a σa的求解本质上是法则四:根之和)
-
φ a \varphi_a φa是渐近线与实轴的夹角( φ a \varphi_a φa的求解满足相角条件)


法则6: 分离点d: ∑ i = 1 n 1 d − p i = ∑ j = 1 m 1 d − z j \sum_{i=1}^n\frac{1}{d-p_i}=\sum_{j=1}^m\frac{1}{d-z_j} ∑i=1nd−pi1=∑j=1md−zj1(对应重根)

- 求分离点的本质是求重根所在的点,根据有重根时式子的特点,有以上推导
- 重根减去极点的倒数之和等于重根减去零点的倒数之和

法则7: 与虚轴交点: { 系统临界稳定点 s = j w 是根的点 \begin{cases}系统临界稳定点\\s=jw是根的点\end{cases} {系统临界稳定点s=jw是根的点

- 临界稳定点与 s = j w s=jw s=jw是根的点无本质区别
- 若渐近线过虚轴,则虚轴上必有对应的根(根轨迹的连续性)
- 令 D ( j w ) = 0 D(jw)=0 D(jw)=0,也就是在 s = j w s=jw s=jw处的特征方程为零,求出的根即为根轨迹与虚轴的交点
法则8: 出射角/入射角: ∑ j = 1 m ∠ ( s − z j ) − ∑ i = 1 n ∠ ( s − p i ) = ( 2 k + 1 ) π \sum_{j=1}^m\angle(s-z_j)-\sum_{i=1}^n\angle(s-p_i)=(2k+1)\pi ∑j=1m∠(s−zj)−∑i=1n∠(s−pi)=(2k+1)π
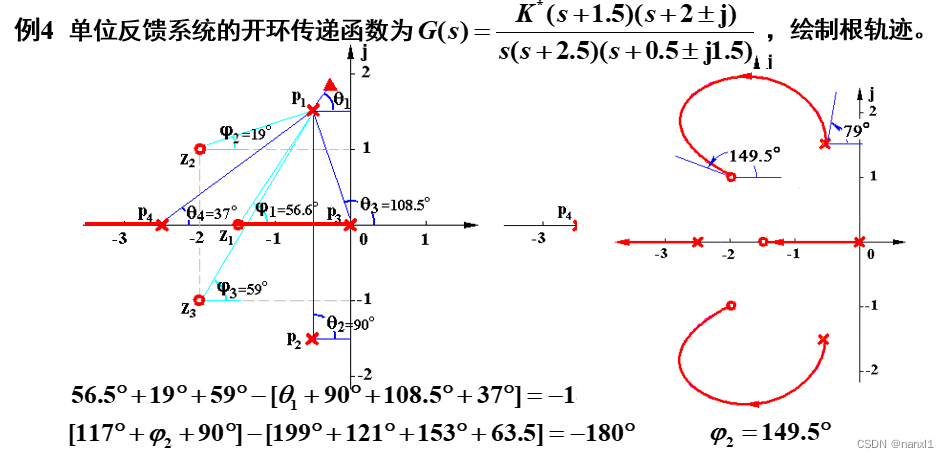
- 即满足相角条件
广义根轨迹
参数根轨迹
除 K ∗ K^* K∗之外其他参数变化时系统的根轨迹
例题

零度根轨迹
系统实质上处于正反馈时的根轨迹

-
仅相角条件改变
-
对应绘制根轨迹的法则3、5、8改变(都与相角条件有关)
例题


关于根轨迹对称性的一个定理
若开环零极点均为偶数个,且关于一条平行于虚轴的直线左右对称分布,则根轨迹一定关于该直线左右对称。

总结
-
关于根轨迹,首先得区分零点、极点、根的概念
-
零点、极点、根其实是复变函数中的概率
-
根轨迹法中的零点极点指的开环传递函数的零点极点
-
根则是令闭环传递函数的特征根 D ( s ) = 0 D(s)=0 D(s)=0, 也是闭环传递函数的极点
-
从这个角度根轨迹其实就是闭环传递函数极点的轨迹
-
而在之前的学习中,我们知道复域中每个极点都对应时域响应中的一个模态
-
因此随着极点的变化,系统的响应也发生变化
-
而与极点类似,零点对系统的响应也产生影响
-
-
关于根轨迹的绘制
- 根轨迹的核心是 D ( s ) = 0 D(s)=0 D(s)=0,对于 180 ° 180° 180°根轨迹有 G ( s ) = 1 G(s)=1 G(s)=1,对于 0 ° 0° 0°根轨迹有 G ( s ) = − 1 G(s)=-1 G(s)=−1, 它们仅是相角条件不同
- 模值条件
∣ G ( s ) H ( s ) ∣ = K ∗ ∣ s − z 1 ∣ . . . ∣ s − z m ∣ ∣ s − p 1 ∣ ∣ s − p 2 ∣ . . . ∣ s − p n ∣ = K ∗ ∏ i = 1 m ∣ s − z i ∣ ∏ j = 1 n ∣ s − p j ∣ = 1 模值条件 |G(s)H(s)|=\frac{K^*|s-z_1|...|s-z_m|}{|s-p_1||s-p_2|...|s-p_n|}=\frac{K^*\prod_{i=1}^m|s-z_i|}{\prod_{j=1}^n|s-p_j|}=1\quad模值条件\\ ∣G(s)H(s)∣=∣s−p1∣∣s−p2∣...∣s−pn∣K∗∣s−z1∣...∣s−zm∣=∏j=1n∣s−pj∣K∗∏i=1m∣s−zi∣=1模值条件
-
相角条件
∠ G ( s ) H ( s ) = ∑ i = 1 m ∠ ( s − z i ) − ∑ j = 1 n ∠ ( s − p i ) = ( 2 k + 1 ) π 相角条件 \angle G(s)H(s)=\sum_{i=1}^m\angle(s-z_i)-\sum_{j=1}^n\angle(s-p_i)=(2k+1)\pi\quad相角条件\\ ∠G(s)H(s)=i=1∑m∠(s−zi)−j=1∑n∠(s−pi)=(2k+1)π相角条件 -
8大基本法则需掌握
-
在分析系统性能时,常用有(求分离点对应的 K ∗ K^* K∗)
K ∗ = ∏ j = 1 n ∣ s − p j ∣ ∏ i = 1 m ∣ s − z i ∣ K^*=\frac{\prod_{j=1}^n|s-p_j|}{\prod_{i=1}^m|s-z_i|} K∗=∏i=1m∣s−zi∣∏j=1n∣s−pj∣
-
根轨迹法相较于时域法,直接根据系统复域的值(零点极点)大致分析系统的性能, 是复域分析的一种方法(不用拉式反变换)








 根轨迹法是一种分析控制系统性能和稳定性的图解方法,通过研究系统参数变化时根轨迹的变化。它涉及到模值条件和相角条件,例如,当开环传递函数为G(s)=K*s/(s+2),随着开环增益K变化,根轨迹描述了闭环系统特征根在s平面上的移动。根轨迹起点始于开环极点,终点止于开环零点,且满足一定的分支数、对称性和连续性法则。此外,根轨迹的渐近线、分离点、与虚轴的交点等特性也对系统性能有重要影响。
根轨迹法是一种分析控制系统性能和稳定性的图解方法,通过研究系统参数变化时根轨迹的变化。它涉及到模值条件和相角条件,例如,当开环传递函数为G(s)=K*s/(s+2),随着开环增益K变化,根轨迹描述了闭环系统特征根在s平面上的移动。根轨迹起点始于开环极点,终点止于开环零点,且满足一定的分支数、对称性和连续性法则。此外,根轨迹的渐近线、分离点、与虚轴的交点等特性也对系统性能有重要影响。
















 1242
1242

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








