GPS抽稀之道格拉斯-普克(Douglas-Peuker)算法
道格拉斯-普克算法是我们常用的一种轨迹点的抽稀算法,抽稀出来的点可以尽可能的维持原先轨迹点的大体轮廓,剔除一些非必要的点。
道格拉斯-普克原理
假设在平面坐标系上有一条由N个坐标点组成的曲线,已设定一个阈值epsilon。
(1)首先,将起始点与结束点用直线连接, 再找出到该直线的距离最大,同时又大于阈值epsilon的点并记录下该点的位置(这里暂且称其为最大阈值点),如图所示:
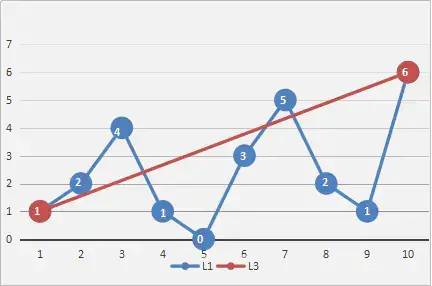
(2)接着,以该点为分界点,将整条曲线分割成两段(这里暂且称之为左曲线和右曲线),将这两段曲线想象成独立的曲线然后重复操作(1),找出两边的最大阈值点,如图所示:
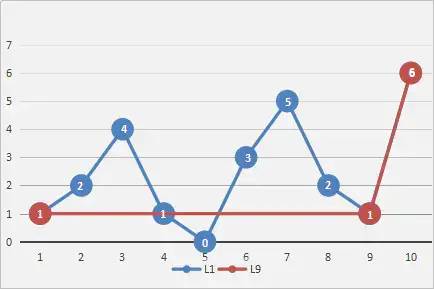
(3)最后,重复操作(2)(1)直至再也找不到最大阈值点为止,然后将所有最大阈值点按顺序连接起来便可以得到一条更简化的,更平滑的,与原曲线十分近似的曲线,如图所示:
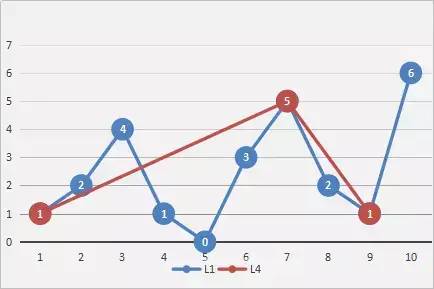
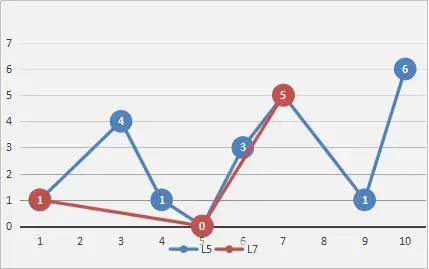
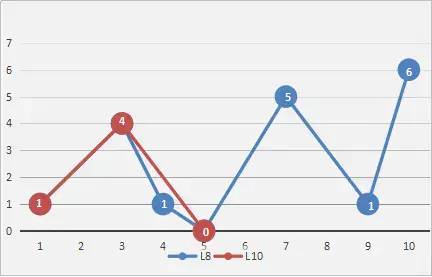
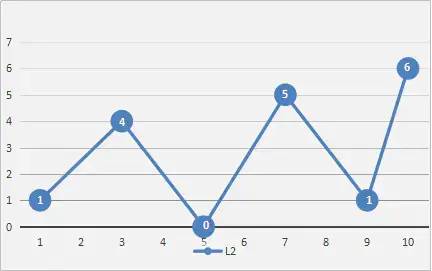
具体思路
对每一条曲线的首末点虚连一条直线,求所有点与直线的距离,并找出最大距离值dmax,用dmax与限差D相比;若dmax < D,这条曲线上的中间点所有舍去;若dmax ≥D,保留dmax 相应的坐标点,并以该点为界,把曲线分为两部分,对这两部分反复使用该方法。控制限差值的大小可以控制抽稀的粒度。
Matlab代码实现:
%% 主函数入口(在该函数界面下点击运行实验)
clc;clear;close all;
points(:,1) = 5:5:300; %x值为1到60
points(:,2) = 10 + 3 * rand(60,1); %y为10加一个0到1的随机数
points(25:35,2) = 5 + 3 * rand(11,1); %其中第25到第35个点低一点
% =========================================================================
[r,c] = size(points);
A(1,1) = points(1,1); A(1,2) = points(1,2);
A(2,1) = points(r,1); A(2,2) = points(r,2);
Threshold = 3; %给定阈值
[A] = ARecursionFun(points,A,Threshold); % 递归
A = sortrows(A,1);
figure(1); %创建图层
plot(points(:,1),points(:,2),'-k'); %绘制原始折线
hold on; %保留当前图层的要素
plot(A(:,1),A(:,2),'*-r'); %在原图基础上绘制特征点
title(['阈值为:',num2str(Threshold)]);% 输入两个相邻特征点之间的扫描线pointsTab,特征点表A(A是折线首尾两个端点)
% 输出补充新发现的特征点后的特征点表A
% 函数名称为ARecursionFun(一个递归函数)
function [A] = ARecursionFun(pointsTab,A,Threshold)
[r,~] = size(pointsTab); % 获取扫描线片段上点的个数
if r > 2 % 如果这条扫描线片段上点数大于2则执行操作
Q1 = [pointsTab(1,1);pointsTab(1,2)]; % 起点坐标对的列向量表示(为了便于点到直线距离计算的表示方法)
Q2 = [pointsTab(r,1);pointsTab(r,2)]; % 终点坐标对的列向量表示(作用同上)
% 遍历这个扫描线,依次计算每个点到扫描线起点终点连线的距离==================
for i = 1:1:r
P = [pointsTab(i,1);pointsTab(i,2)]; % 当前点坐标的列向量表示
d(i,1) = abs(det([Q2-Q1,P-Q1]))/norm(Q2-Q1); % 计算点到直线的距离
end
% 计算完毕,每个点到直线的距离存入列向量d中================================
if max(d) > Threshold % 如果距离列向量中最大值大于阈值则进行下述操作
ind = find(all(repmat(max(d),size(d,1),1)==d,2)); % 获取列向量中最大值对应的点的序号
[rA,~] = size(A); % 获取当前特征点表A已存点的个数
A(rA+1,1) = pointsTab(ind,1); % 将这个点作为特征点存储起来(x坐标)
A(rA+1,2) = pointsTab(ind,2); % 将这个点作为特征点存储起来(y坐标)
pointsTabb = pointsTab(1:ind,:); % 以刚才存储的特征点为界限,起点到该点建立新的片段扫描线
A = ARecursionFun(pointsTabb,A,Threshold); % 函数自身调用进行递归,进一步获取片段内的特征点
pointsTabe = pointsTab(ind:r,:); % 以刚才存储的特征点为界限,该点到终点建立新的片段扫描线
A = ARecursionFun(pointsTabe,A,Threshold); % 函数自身调用进行递归,进一步获取片段内的特征点
end
end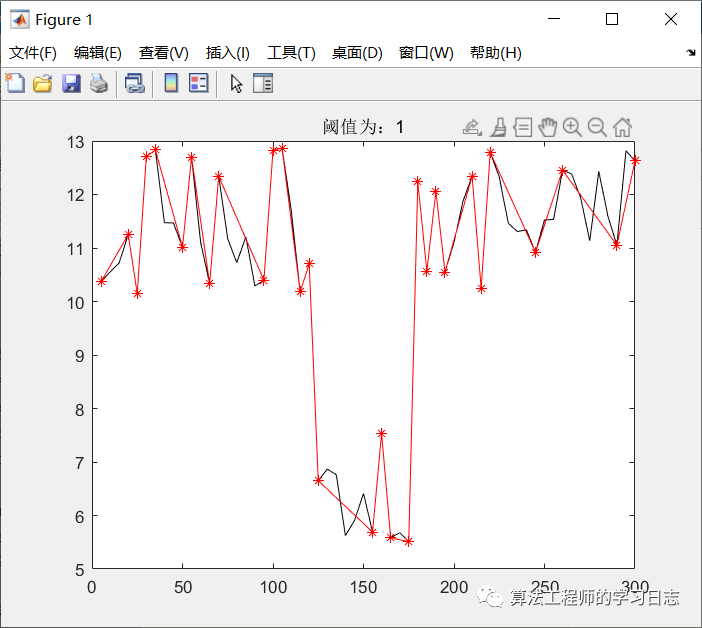

























 533
533











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








