Modman:一直先进的无性别连接器可重构机器人系统和自运动学建模方法

最新推荐文章于 2024-04-26 18:33:29 发布

hello我是小菜鸡

最新推荐文章于 2024-04-26 18:33:29 发布

阅读量262

点赞数

文章标签：重构机器人

原文链接：https://ieeexplore.ieee.org/abstract/document/9093087/

版权

1. 摘要

随着生产生命周期的日益缩短，对高适应性系统的需求日益增加。在这种趋势下，可重构机械臂以其高适应性和易于维护的特点，成为取代传统非可重构机械臂的有力替代。然而，大多数现有的可重构机器人都是为非工业用途而设计的，并且由于其精度低和低机械/电气能力而停留在实验室水平。在这篇论文中，我们展示了我们新开发的手动可重构机械臂，ModMan，并且配备了无性别连接器，具有高机械/电气能力和多自由度模块，这将增加可能的配置数量，同时最大限度地减少机械臂性能的损失。针对可重构机械臂无性别连接和多自由度模块的复杂性，提出了一种可重构机械臂的自动运动学建模算法。对六自由度构型的可重复性进行了评估，证明ModMan的性能与现有的非重构机械手相当。对任意连接的模块进行了运动学重构实验。

2. 介绍

对基于个人需求的改进机械的需求不断升级，有利于工业4.0的原则，促进了更高水平的适应性。传统的工业用固定构型的机械手，在本文中被称为不可重构机械手，通常被用来满足这种要求，并且总体上显示出令人满意的性能。然而，它们的工作空间被限制在固定的体积内，并且就时间和功耗等几个性能指标而言，它们可能不是某些任务的最佳选择。此外，由于只有专业人员才能对非可重构机械臂进行修复，因此从硬件故障中恢复需要花费大量时间。为了克服不可重构机械手的这些弱点，文献中引入并研究了可重构机械手，使用户能够配置自己的最佳机械手，并轻松更换损坏的部件，以便从故障中快速恢复[1]。

模块化指的是系统组件可以分离和重组的程度，这样每个部分的复杂性可以被隐藏，并且可以简单地与其他部分进行接口，如[2]所述。在模块化机器人设计中，本文从可重构度（Degree of Reconfigurability, DOR）的概念来定义模块化，可重构度指的是机器人可能组合的数量与模块数量的关系。在具有相同运动结构的机械手中，如果具有较少的零件数量和较好的性能指标，则认为该机械手具有较高的完整性。因此，一个不可重构的机器人被认为具有最高的完整性。设计一个良好的模块化机械臂系统相当于增加DOR和完整性，然而，DOR和完整性之间存在着内在的权衡。更高的DOR通常是通过增加连接端口的数量和模块的种类来实现的，这会同时降低完整性。在本文中，我们提出在模块化机器人系统中应用无性别连接器和多自由度模块来弥补这一缺陷。无性别连接器将DOR增加到模块数量的2倍。多自由度关节通过减少零件和连接器空间来提高完整性，并且易于缩小尺寸[3]。

对模块化机器人研究文献的广泛调查[4]-[7]表明，大多数此类文献是关于自重构模块化机器人的。这种机器人具有独立的调节器，用于自我重新配置功能以形成所需的配置。然而，与功能相关的部件由于占用了大量的空间和重量，降低了机器人的完整性。因此，对于工业应用而言，具有更高完整性的手动可重构模块化机械臂将优于自重构模块化机械臂。

当前已经有几次尝试开发一种适合工业应用的手动可重构模块化机器人机械手。可重构模块化机械臂系统（Reconfigurable Modular Manipulator System, RMMS）[8]，[9]是这种机械臂最早的实现之一。Schunk已经开发并商业化了LWA系列[10]，手动可重构机械手，包括2个自由度模块，Powerball。最近，Acutronic Robotics公司推出了模块化关节式机械臂(MARA)和硬件机器人操作系统(H-ROS)[11]。虽然机器人是手动可重构的机械手，但由于它们的性别连接，它们的DOR有限。

可重构机械手的一个关键设计特点是连接器。在[12]中，为模块化机器人Thor提供了一个基于弹簧加载引脚的无性别连接器，用于电信号。文献[13]提出了一种具有机械连接机构的无性连接器HiGen。HiGen采用围绕中心轴的四个挂钩进行机械连接，并采用圆形弹簧销阵列进行电气连接。然而，无性别连接器的机械和电气连接对于工业应用来说不够强大，并且由于弹簧引脚数量少，它们的低电流能力。在我们之前的工作[14]，[15]中，提出了一种无性别连接器，具有坚固的机械设计和有效的弹簧销布局。本文在前人工作的基础上，提出了一种优化的无性连接器，其性能能够满足工业应用。

随着模块化机器人机械手硬件设计的进步，模块化机器人机械手软件设计也有了相应的进步，尤其是在运动学方面。文献[16]提出了一种采用Denavit-Hartenberg (DH)参数表示的模块化机器人机械手运动学建模方法。然而，这种表示对于模块化机器人机械手来说是不够的，因为当连接发生变化时，需要重新定义每个链路帧。在[17]中，提出了模块化机器人机械手运动学的现代螺旋理论表示。他们根据装配关联矩阵（AIM）和可及性矩阵（AM）定义了连接，以表示模块之间的连接方式，并以坐标无关的方式描述其机械手的运动学。在[18]中，定义了模块组装的连接器图表示，以在每个连接处添加偏移角度值。上述研究都有一个共同的局限性;它们的每个联合模块都是1自由度的，具有固定的输入输出端口。因此，在运动学建模中需要考虑多自由度、多连接端口的关节模块。在[3]中，引入了自适应机器人系统架构（ARSA），通过定义包含模块特定的运动学/动力学参数的对象关联矩阵（OIM）来处理更一般类型的模块和模块之间的连接。然而，目前还没有针对这种结构提出系统的运动学建模算法。

在这方面，本工作的贡献是在硬件和软件方面显著提高了可重构模块化操作器的完整性。在硬件方面，在我们之前的作品[14]的基础上，扩展了模块设计，并进一步优化了连接器。由于具有2自由度，新的关节模块具有更好的完整性。与之前的版本[14]相比，本文提出的无源连接器可以承受更大的机械力，并通过引脚布局优化传输更多的电力。在软件方面，我们引入了一种新的自动运动学建模算法，该算法可以检测任意树结构的运动结构并相应地建立运动模型。通过仔细识别连接相关参数和模块内部参数，利用通过连接器传输的最小信息量有效地建立运动学模型。作为一个完整的系统来展示所开发的组件的集成，我们构建了一个模块化的机械手系统，命名为ModMan。

3. 可重构机器人机械手的硬件开发

在本节中，介绍了构建ModMan系统各模块的硬件组成。一种无性连接器，授予美国专利[19]，开发了足够的机械/电气能力，以承受6或7自由度机械手的负载。关节单元是一组与1-DOF相对应的零件，本文也给出了关节单元的细节。在此基础上，构建了7种类型的关节模块、2种类型的连杆模块和1种类型的夹持模块。

A. 无性的连接器

ModMan无性连接器由机械连接机构和电气连接组成，如图1所示。为了使关节模块具有不同的运动范围，连接器被设计为可在每90°角度连接4个不同的偏移角度。

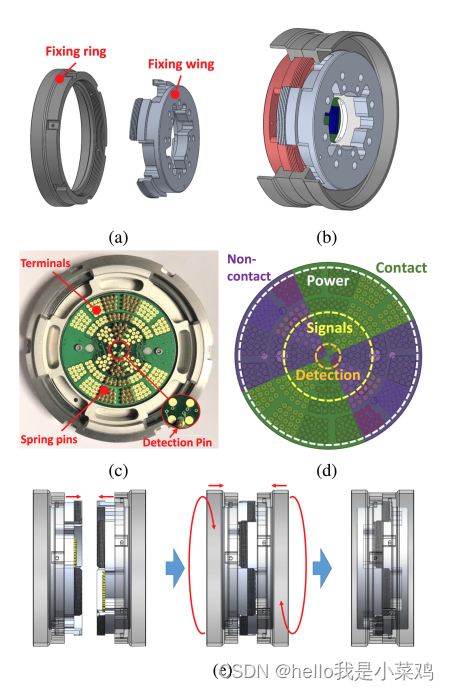
图1所示。无性别连接器:(a)固定环和翼，(b)机械连接，(c)弹簧销和端子的布置，(d)电气连接，(e)连接图。

为了直观、牢固的连接，机械连接机构采用具有挤压特征的简单螺钉紧固件，如图1a所示。该紧固件由内螺纹固定环和外螺纹固定翼组成。如图1e所示，每个固定翼都用另一侧的固定环固定。图1b所示的紧固结构可以承受各个方向的弯曲和扭转应力。请注意，两个固定翼之间的机械连接是滑动配合，以尽量减少连接时的误差和间隙。虽然可以用手拧紧紧固件，但最好使用钩扳手，以确保良好的连接。

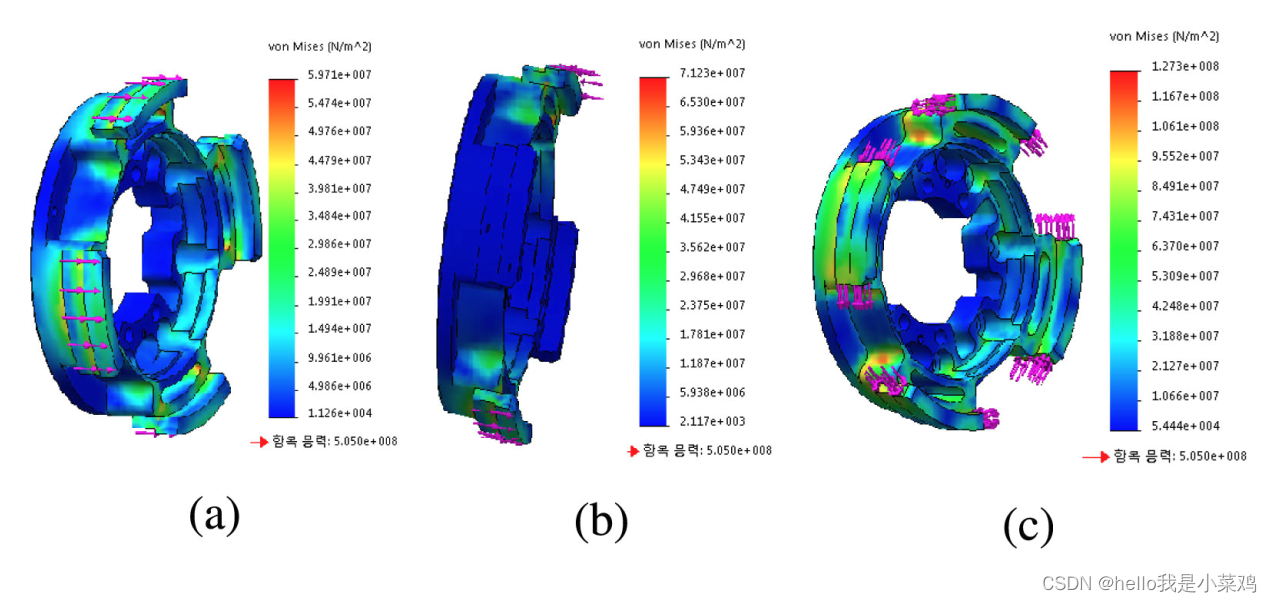
为保证ModMan的结构安全，在SolidWorks上应用有限元法对固定翼刚度进行分析，结果如图2所示。对固定翼施加1,000 N的极高拉力，产生的最大应力为5.97 × 107 N/m2，相关安全系数(FoS)为8.46。对固定翼施加160 Nm的扭矩——大关节模块的最大峰值扭矩(表2)，由此产生的径向和轴向最大应力分别为7.12 × 107 N/m2和1.27 × 108 N/m2，其相关FoS分别为7.09和4.97。由于这些结果仅针对单个固定翼，因此由两个固定翼和环组成的总成的实际FoS至少要增加一倍。所有这些结果都保证了机械连接的几何结构在各个方向上都是安全的。需要注意的是，我们之前的版本[14]在相同的径向拉力和扭转下，FoS分别为2.81和2.70，且轴向扭转时的最大应力超过了结构的屈服强度。结果表明，该方案的结构强度优于原方案。

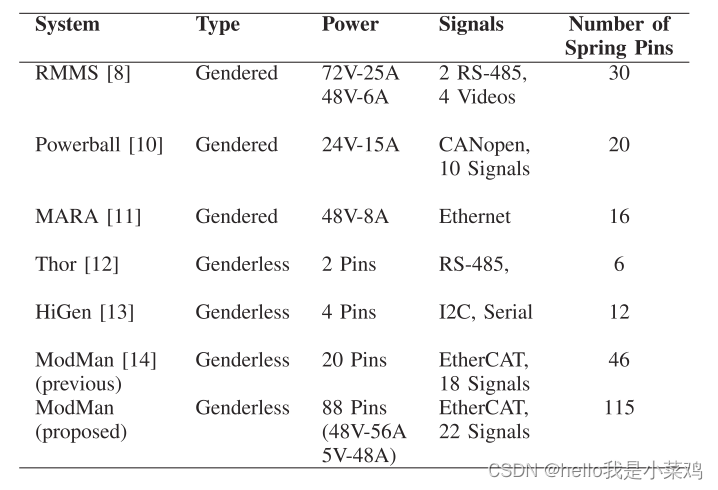
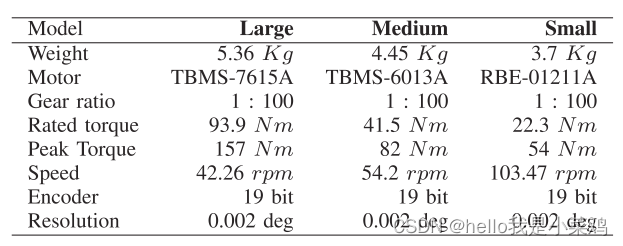
图2所示。有限元结果:(a) 1000 N的拉力，(b)径向扭转，(c)轴向扭转为160 Nm。

无性别连接器的电气连接(图1c)负责在模块之间传输电力和通信信号。弹簧销钉和表面端子之间的接触用于连接，以保证对机械间隙的稳健性。如图1d所示，电气连接分为三个部分:内部部分为识别偏置角的检测引脚，中间部分为包括EtherCAT (Ethernet for Control Automation Technology)信号在内的26个信号，外部部分为电源和地。为了使连接在每90◦，并最大限度地增加接触的数量，弹簧引脚被安排在两个截然相反的八角形。请注意，检测引脚位于仅为90◦分辨率的八分之一。两组表面端子以排列的镜像图案排列，并以±45°角度放置。根据有效设计的布局，总共有115个弹簧销安装在连接器上。有了这么多的弹簧引脚，ModMan无性连接器可以比其他连接器传输更多的功率和信号，如表1所示。Mod- Man无性别连接器的性能能够支持高自由度配置的负载，例如双臂配置。

B. 关节组件

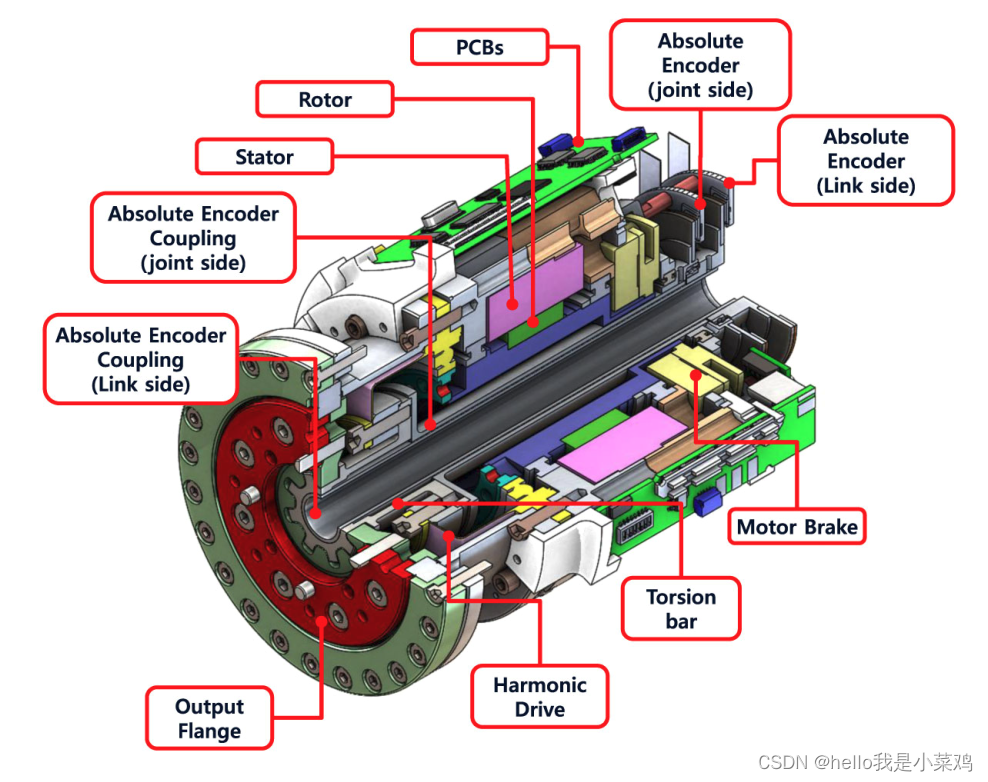
为ModMan开发了不同尺寸(小、中、大)但结构相同的关节单元，大关节单元示例如图3所示。关节单元的结构与[20]中介绍的作动单元有一些共同的特点。节理单元的设计主要着眼于最优间距。关节侧和连杆侧的位移通过联轴器传递到输出法兰的另一侧，并使用两个绝对编码器进行测量。无性别连接器将连接在输出法兰上，出于安全考虑，电机后面放置一个电机制动器。每个接头单元的详细规格如表2所示。

为了有效地管理和开发模块，三种类型的pcb以模块化的方式开发;用于计算的控制器pcb，用于通信的EtherCAT pcb，以及用于放大电机输入的电机驱动器pcb。由于EtherCAT通信协议具有数据进/出端口的方向性，因此实现了切换电路来改变EtherCAT通信的方向。所有类型的设计都具有相同的几何形状，并且可以通过柔性电缆相互连接，以便一组pcb可以绕在接头上，从而最大限度地减少安装它们所需的空间。

为了配置不同类型的机械手，开发了几种类型的关节模块，如图4所示。为了构建一个2-DOF模块，两个相同尺寸的关节单元可以有无限多种组装方式，但我们选择了两种在正交方向上有偏移的组装方式，我们将其标记为“a型”和“B型”。总共有六个2-DOF模块，由两种不同的类型和三种不同的尺寸组成。通过使用所有6个2-DOF模块，我们可以构建两个典型的机械手——“左”臂和“右”臂——这将在后面展示。

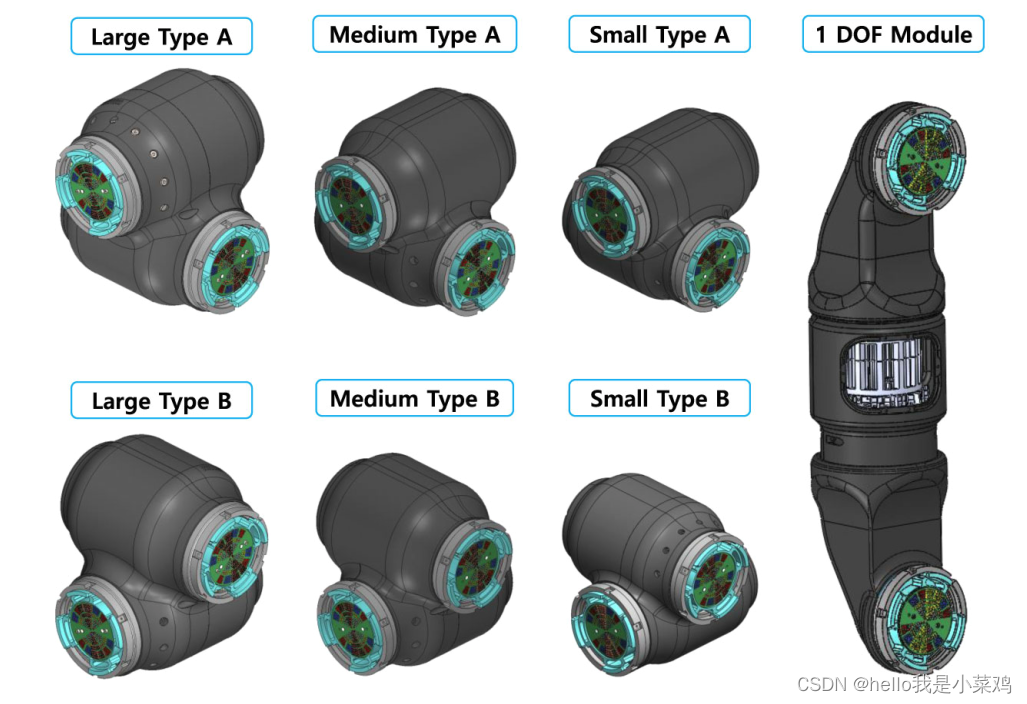
除了2-DOF关节模块外，还开发了1-DOF关节模块，如图4所示，其关节单元与大尺寸2-DOF关节模块相同。在第一个2-DOF关节模块之后进行组装，以配置典型的7-DOF机械手。

C. 链接和抓取模块

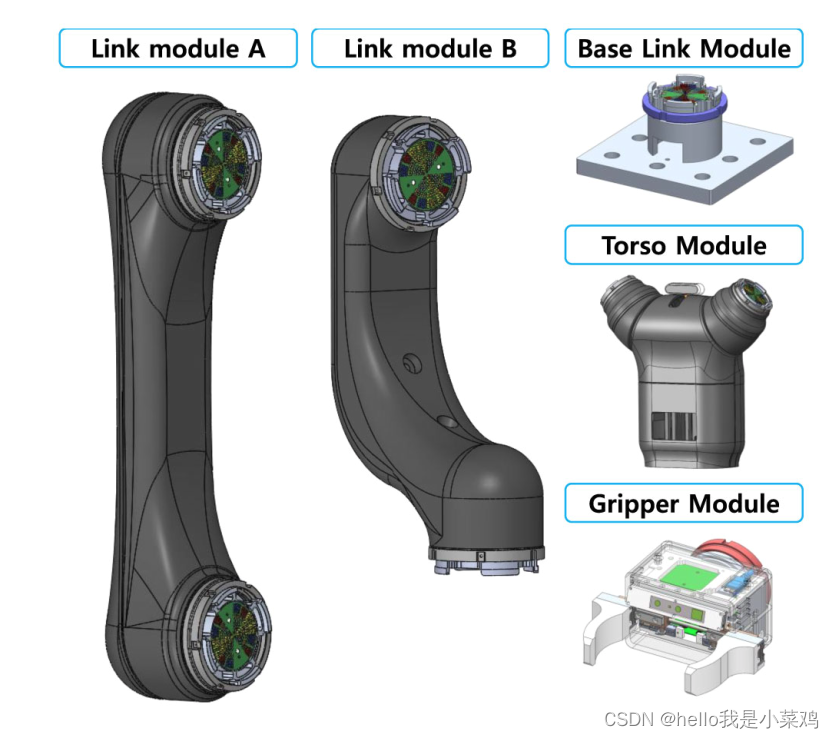
除了关节模块外，还开发了四个链接模块(每个模块都具有无性别的连接器)来配置各种类型的机械手，如图5所示。“链接模块A”和“链接模块B”分别为上臂和下臂设计。同样，“基础链接模块”和“躯干”分别设计为单臂和类似人的双臂配置。请注意，即使没有任何执行器，链路模块也像一个奴隶，因为它们的连接方向和角度需要自动检测并考虑运动学重构。因此，每个链路模块都有一个控制器和一个EtherCAT pcb。链路模块A和链路模块B的重量分别为3.88 Kg和3.4 Kg。

为了验证概念，我们还设计了如图5所示的夹持器模块。除了低级控制器和EtherCAT PCB外，夹持器还具有用于驱动的PCB。夹持器模块的钳口彼此耦合，由单个执行机构驱动。它具有检测夹持力的功能，利用弹簧挠度来拾取柔软的物体。抓手还利用RGB-D传感器(RealSense SR300)来执行简单的基于视觉的拾取任务。

4. 机械臂自动建模

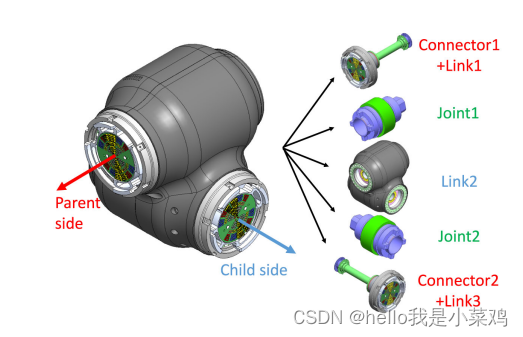
由于ModMan系统基于无性别的连接器和多自由度关节模块，因此ModMan的运动学建模需要额外考虑如何将模块分解为关节/链接元素。例如，最小连接器数的2自由度关节模块由3个链路单元、2个关节单元和2个连接端口组成，如图6所示。鉴于这些考虑，我们开发了一种用于树形结构可重构机械手的自动运动学建模算法，并将其应用于ModMan。

A. 运动学建模

接下来，我们将使用现代螺旋理论的运动学公式，如[21]、[22]所述。机器人的任务空间可以定义在特殊欧氏群SE(3)的空间上，4 × 4刚体变换矩阵T∈SE(3)的形式为

$T=\begin{bmatrix} R & x\\ o_{1 \times 3} & 1 \end{bmatrix},$ （1）

其中， $R$ 是一个3X3的旋转矩阵， $x \in \mathbb{R}^{3}$ 是位置矩阵。对于任意 $T \in SE(3)$ ，可以找到一组对应的旋转参数 $A \in \mathbb{R}^{6}=\left ( \omega ^{T},v^{T} \right )^{T}, \omega,v \in \mathbb{R}^{3}$ ,其满足矩阵指数形式：

$T=e^{\left [ A \right ]},$ （2）

旋进参数A里的方括号里[A]为

$\left [ A \right ]=\begin{bmatrix} \left [ \omega \right ] & v \\ 0_{1 \times 3} & 0 \end{bmatrix},$ (3)

这里，对于三维向量 $\omega =\left ( \omega _1, \omega _2, \omega _3 \right )^T$ 的方括号符号 $\left [ \omega \right ]$ 是

$\left [\omega \right ]=\begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1\\ -\omega_2 & \omega_1 & 0 \end{bmatrix}.$ (4)

为了找到一种系统的树形结构可重构装配机械臂的运动学建模方法，我们首先定义了一个广义模块，如图7所示。假设它是对应分支中的第 $i$ 个模块，则广义模块本身是一个树形结构，由 $P^{i}$ 个连接端口（每个端口可以连接到父端也可以连接到子端）和 $K^{i}$ 个连接单元组成，连接单元的旋进参数为 $A_{J}^{i} \in \mathbb{R}^6,J=1,\cdots ,K^{i}$ ，在模块框架 $\left \{ i \right \}$ 中描述。关节单元被假定为转动关节或移动关节。尽管可以用与文献[23]中描述的1自由度更高的关节单元类似的方式来处理，但由于它们在工业机械臂中的稀缺性，这里不考虑它们。

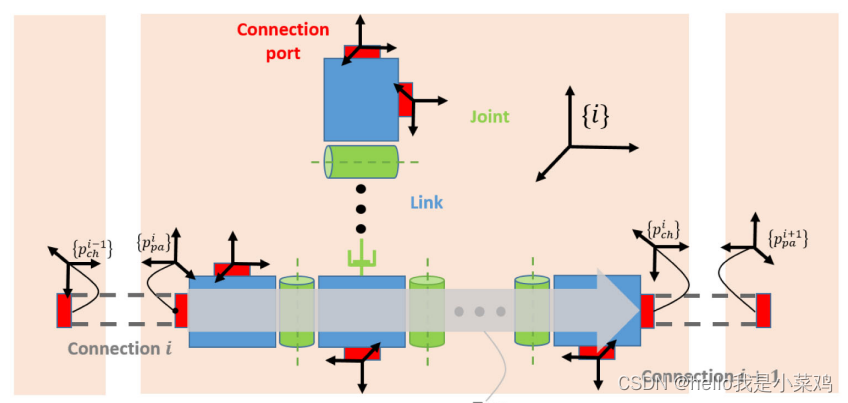
对于一个串行连接，广义模块 $i$ 可以有 $S^{i}=P^{i}(P^{i}-1)$ 个可能的排列。当进行串行连接时，可以检索唯一分支，并将其表示为形式为 $B_{s}^{i}=\left \{ pa_{s},J_{s,1},\cdots ,J_{s,k^{i}},ch_{s} \right \},s=1,\cdots ,S^{i}$ ，其中 $pa_{s}$ 为父端连接端口索引， $ch_{s}$ 为子端连接端口索引， $J_{s,j},j=1,\cdots ,k^i$ 为分支有效节点个数为 $k^i$ 的对应节点单元的指标。一旦连通，具有 $k^i$ 个有效连接元素和 $k^i + 1$ 个连接元素的唯一分支索引 $s$ 。

假设 $m$ 个模块串联构成一个 $n$ 自由度机械手，每个模块有自己的模块框架 $\left \{ i \right \},i=1,\cdots ,m$ 。正运动学 $T_{0,e}$ 是从基坐标系 $\left \{ 0 \right \}$ 到末端执行器坐标系 $\left \{ e \right \}$ 的变换，可以表示为：

$T_{0,e}=T_{0,p_{pa}^{1}}T_{p_{pa}^{1},p_{pa}^{2}}\cdots T_{p_{pa}^{m-1},p_{pa}^{m}} T_{p_{pa}^{m},e}$ (5)

其中 $T_{p_{pa}^{i},p_{pa}^{i+1}} \in SE(3)$ 为模块 $i$ 的模块化运动学，是模块 $i$ 的父端口框架 $\left \{ p_{pa}^i \right \}$ 到模块 $i+1$ 的父端口框架 $\left \{ p_{pa}^{i+1} \right \}$ 的变换矩阵。 $T_{p_{pa}^{m},e} \in SE(3)$ 是定义在末端执行器模块的变换矩阵。假设所有链接帧最初都与模块帧 $\left \{ i \right \},T_{i,l}$ 重合，则模块帧 $\left \{ i \right \}$ 到链接元素帧 $\left \{ l \right \},l=0,\cdots ,k_i$ 可以被描述为

$T_{i,l}=\left\{\begin{matrix} I_{4 \times 4}, & l=0\\ e^{\left [ A^{i}_{J_{s,1}} \right ] \theta_{\psi +1}} \cdots e^{\left [ A^{i}_{J_{s,l}} \right ] \theta_{\psi +l}}, & otherwise \end{matrix}\right.$ (6)

其中， $\psi =\sum_{q=1}^{i-1}k_q$ 。现在模块 $i$ 的模运动学可以被描述为

$T_{p_{pa}^i, p_{pa}^{i+1}} =M_{i,p_{pa}^i}^{-1}e^{\left [ A^{i}_{J_{s,1}} \right ] \theta_{\psi +1}}\cdots e^{\left [ A^{i}_{J_{s,k_i}} \right ] \theta_{\psi +k_i}} M_{i,p_{ch}^i} T_{p_{ch}^i,p_{pa}^{i+1}},$ (7)

其中， $M_{i,p_{pa}^i} ,M_{i,p_{ch}^i} \in SE(3)$ 分别是从模块帧 $\left \{ i \right \}$ 到父端口帧 $\left \{ p_{pa}^i \right \}$ ，子端口帧 $\left \{ p_{ch}^i \right \}$ 的初始转换。 $T_{p_{ch}^i,p_{pa}^{i+1}}$ 为第 $i$ 个子端口帧 $\left \{ p_{ch}^i \right \}$ 到第 $i+1$ 个父端口帧 $\left \{ p_{pa}^{i+1}\right \}$ 的变换，其值与模块 $i$ 与模块 $i+1$ 之间的偏移角 $\phi _i$ 有关。为了系统地推导 $T_{p_{ch}^i,p_{pa}^{i+1}}$ ，我们假设在每个连接端口都有不同的参照系，并且参照系的方向以一致的方式定义；本文选择连接口的外法线方向为 $\hat{z}-$ 向，偏置角的参考线方向为 $\hat{x}-$ 向。现在 $T_{p_{ch}^i,p_{pa}^{i+1}}$ 可被定义为：

$T_{p_{ch}^i,p_{pa}^{i+1}}=\begin{bmatrix} cos\phi_i & sin \phi_i & 0 &0 \\ sin \phi_i & -cos \phi_i & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}.$ (8)

旋进理论运动学的一个优点是，通过将每个关节的螺杆参数的参考坐标转换为末端执行器框架，可以有效地计算机械手雅可比矩阵[21]。

B.模型参数辨识

上述模型参数需要分为两组;模块固有参数和连接相关参数。模块固有参数其值应在连接之前提供，为

（1） $M_{i,p_q^i} \in SE(3),q=1,\cdots ,P^i$ ，从模块帧 $\left \{ i \right \}$ 至连接端口帧 $\left \{ p_q^i \right \}$ 的初始转移矩阵，

（2） $A_j^i \in \mathbb{R}^6, J =1,\cdots ,K^i$ ，模块帧 $\left \{ i \right \}$ 中描述连接单元的旋进参数，

（3） $B_s^i = \left \{ pa_s^i,J_{s,1}^i, \cdots J_{s,k^i}^i,ch_s^i \right \},s=1,\cdots ,S^i$ 所有可能的分支，以对应父端口、联合元素和子端口的一系列索引的形式表示。

依赖于连接的参数（其值由连接决定）为

（1） $t$ ，模块的ID，

（2） $S$ ，运动学树的索引,

（3） $\phi$ ，连接的偏移角。

请注意，由于可能排列的数量 $S^i$ 与连接端口数量 $P^i$ 的平方成正比，因此可以将 $B_s^i$ 视为一个内在参数。端口数量较少的模块，如ModMan模块，其 $S^i$ 值较小。因此，在连接之前，每个分支都有 $B_s^i$ 的值，在连接时识别分支ID是有效的。对于具有许多连接端口的模块，模块本身应该能够在建立连接时自动检索分支 $B_s^i$ 。

在本研究中，连接相关参数遵循5位整数协议，如图8所示。前3位代表模块号，第4位和第5位分别代表树号和偏移角度。现在，已配置的机械手的连接状态可以表示为一系列整数。图8示出了一个6自由度右臂构型的例子。

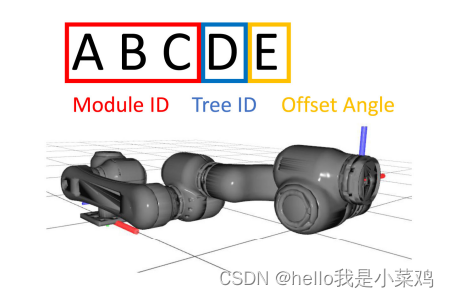
图8 连接协议和配置机械手在其零位与00010-21114 - 00212- 22214-00512- 23112- 00101 (base-LargeA-LinkA-MedB-LinkB-SmallA-Dummy)。

已开发模块的可能配置示例如图9所示。由于每个模块都可以表示为广义模块，因此本文算法不仅支持关节+连杆连接，还支持连杆+连杆或关节+关节连接，如连接7自由度机械臂中出现的2自由度大模块+ 1自由度模块。

通过上述过程得到的运动学模型可用于执行任务空间中定义的动作，并表征机器人的工作空间。由于可重构机器人的特性，其运动学逆解和工作空间表征方法应适用于一般的运动学结构；例如[21]中描述的Newton-Raphson数值逆运动学和[24]中描述的工作空间边界确定。

5. 实验

我们做了两个不同的硬件实验。通过精度评估，证明了六自由度ModMan系统的可重复性与非可重构机械臂相当。我们还进行了重新配置测试，以查看前一节中提出的自动运动学建模算法的有效性。

A. 系统设置

为了验证ModMan与传统机械手相比的性能，我们开发了用于低级控制和高级命令的软件。

对于独立联合控制，采用离散PID控制器进行位置控制。输出为链路侧角，电机输入为脉宽调制(PWM)。一个离散时间一阶低通滤波器，也称为指数加权移动平均，涉及到导数项，并在积分项应用饱和。

为了证明自动运动学建模算法在实际硬件上的有效性，我们还构建了一个软件来可视化ModMan系统。当所有模块都连接上后，每个从机将与连接相关的参数发送给主控制器，主控制器再转发给可视化软件。利用第三节的算法构建机械手的运动学，并通过TCP/IP通信每10 ms接收一次的联合编码器值与硬件同步仿真模型。如图6所示，将一个模块的三维网格模型划分为各个链路单元，所有的链路坐标由Eq.(6)计算。

B. 与非可重构机械臂的重复性比较

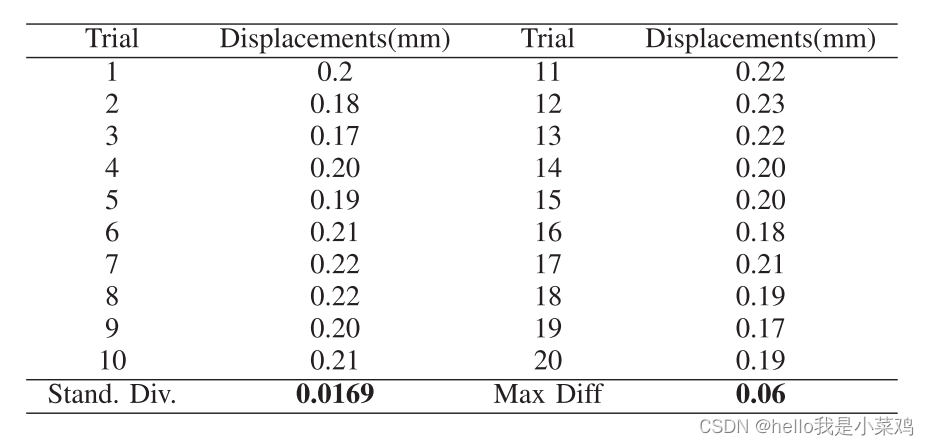
为了评估可重复性，基于梯形关节空间规划器规划的轨迹，左6自由度构型机械臂在两个姿态之间重复运动。当机器人以如图10所示的第二种姿态撞击量规尖端时，记录校准后的刻度盘量规值。结果如表3所示。值间最大差值为0.06 mm，标准差为0.0169 mm。最广泛使用的不可重构机械手之一，Universal Robot的UR5，具有±0.1 mm的重复性[25]。结果表明，在可重复性方面，我们的机械手系统确实可以与现有的不可重构机械手相媲美。注意，ModMan系统只依赖于独立的联合控制。这意味着我们仍有能力提高其可重复性，以用于更精确的应用。

C. 可重构性

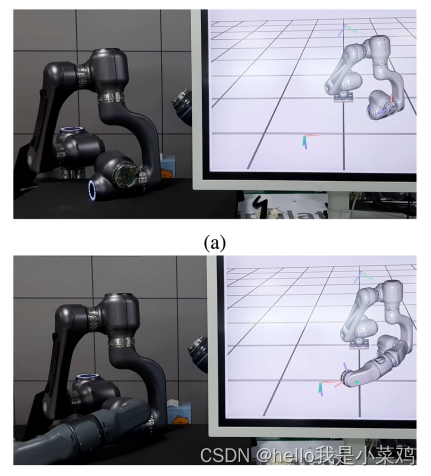
对两种不同的模块组合进行了运动学建模测试，结果如图11所示。第一种构型是6自由度右臂机械臂，它类似于传统的6自由度不可配置机械臂的特性。通过在第一配置的末端连接1-DOF模块形成第二配置。自动运动学建模算法成功地构建了两个机械手的运动学模型;模型与实际的硬件姿势相同。

为了确定机器人雅可比矩阵是否正确，我们还进行了跟踪任务空间轨迹的实验。如III-A节所述，通过将各关节螺杆参数的参考坐标转换为末端执行器框架，可以很容易地获得微分运动学的机械手雅可比矩阵。利用数值逆运动学和b样条插值实现了笛卡尔空间规划。一个7自由度的右臂构型受到一个方向恒定的任务空间轨迹，结果如图12所示。用最小范数解的Moore-Penrose伪逆计算了6 × 7雅可比矩阵的逆。末端执行器在运动过程中成功地保持其方向不变。

图12 计时码表笛卡尔运动7-DOF配置。末端执行器的方向用向上指向的箭头显示。

7. 结论

在本文中，我们提出了一个可重构的机械手系统，ModMan，从硬件到软件。无性别连接器显示高机械/电气能力，能够驱动可重构的机械手多达7个关节元件。ModMan系统有7个关节模块和4个连杆模块，可以组合配置各种类型的机械手，包括广泛使用的6-DOF和7- dof机械手。针对无性别连接和多自由度模块，提出了一种基于广义模块概念的可重构机器人机械臂自动运动学建模算法。实验结果表明，ModMan的重复性与传统工业不可重构机械手相当。ModMan的可重构性也在实际硬件上通过多个模块的任意组合进行了验证。

通过扩展ModMan硬件模块的种类，用户将能够配置各种其他类型的机器人操纵器，如选择性合规装配机器人手臂(SCARA)机器人或球形机器人。同时，该自动运动学建模算法可应用于其他可重构机器人系统。自动动态建模算法将在我们未来的工作中出现，使我们能够提出更复杂的转矩控制算法，并使ModMan能够对外力作出反应以保证安全，从而可以将其视为协作机器人。