摘 要 对无人机气动与隐身联合优化进行了综合评述,并对未来研究进行了展望。首先阐述了目前隐身无人机在复杂飞行环境下的性能挑战,指出了传统设计方法的局限性;随后以无人机气动与隐身联合优化设计为研究对象,将联合优化设计分为基于工程算法的直接优化、基于代理模型的优化以及基于改善流程的优化等三类技术路线,总结了各个优化路线的基本原理、发展历程和最新研究进展,并针对气动隐身联合优化中的共性技术如参数化建模、网格划分等进行了总结与阐述;最后给出了无人机气动隐身联合优化的发展趋势分析。综述表明,无人机的气动与隐身联合优化还需持续开展研究,需重点关注开展基于知识提取-指标驱动的隐身无人机总体设计、利用人工智能方法提升气动与隐身性能评估效益、开展气动与电磁计算网格的一致性应用和针对现有无人机开展隐身强化设计与实现等方面。
关键词 无人机;气动;雷达隐身;代理模型;联合优化;优化设计
1 引 言
随着MQ-25、XQ-58A、XQ-67A等无人机的问世,隐身无人机逐步走入大众视野,成为现代战争中不可或缺的力量[1]。无人机以其低成本、高生存率、无人员伤亡等优势,正改变着战争的形态和战术的运用。在俄乌冲突中,无人机的广泛应用和显著表现充分展示了其在未来战争中的重要地位与潜力。在未来战争有人/无人机协同作战的背景下,无人机需要具备高速、隐身的特性,这使得气动和隐身性能成为评价其任务能力的关键,兼顾气动与隐身性能也成为无人机总体设计的必要选择[2-3]。
伴随着侦察打击技术的不断提升,无人机的使用环境变得复杂严苛,要求无人机具备更高的综合性能。强隐身性依旧是未来无人机不可或缺的关键性能。在雷达隐身设计方面(后文中的隐身均指雷达隐身),外形设计起到主导作用[4-5],而外形设计也直接影响着无人机的气动性能,这是两者可以开展联合优化的物理基础。并且相较有人机,无人机没有载人约束,结构更具有灵活性,这也表示无人机能够提供更大的优化设计空间。气动与隐身联合优化,数学上看是通过参数化建模以及优化建模,将工程上的设计问题转化为最优化问题,避免对设计经验的强依赖[6]。
无人机气动与隐身联合优化可以看作是多学科设计优化的典型应用[7-8]。但针对气动与隐身联合优化的方法总结与技术完善仍不充分。首先,由于专业设置方面的限制,大多数飞机气动设计师并不熟悉电磁场理论,反之熟悉电磁场的研究人员往往不熟悉飞机的气动力分析[5];其二,无人机的气动性能与隐身性能多数情况下是负相关的,例如在翼型的隐身性能优化中,减小尾缘方向角可降低雷达散射截面(Radar Cross Section, RCS),有利于隐身性能,但是翼型的尾部弯度同时关系到气动后加载设计,影响气动性能[9]。
综合来看,无人机的气动与隐身联合优化面临着计算复杂性、模型复杂性、组织复杂性等困难。计算复杂性是指高精度的气动和雷达特性分析都面临着巨大的计算量,尤其针对具有精细结构且采用了复合材料的无人机,它的气动数值计算和电磁散射计算本身变得棘手;模型复杂性是指针对无人机的数字化建模以及参数化表征存在挑战,尤其是具有复杂结构的整机建模;组织复杂性是指无人机的结构外形、气动特性和隐身特性之间存在的强烈非线性使得针对最优解的寻找与求解十分困难。
本文的内容包括:总结无人机气动与隐身联合优化的技术路线;梳理并凝练气动与隐身联合优化的共性关键技术;针对不同的技术路线分析相应的发展现状;最后给出了气动与隐身联合优化的发展趋势分析。
2 提高优化效益的技术路线梳理
无人机气动隐身的联合优化本质上是采用单级优化方法的多学科优化,优化过程中需要考虑到不同学科之间的耦合。学科间的典型耦合关系如图1所示,X1、X2分别为学科1、学科2的输入变量,Y1、Y2为学科1、学科2的输出变量,G1、G2为学科1和学科2之间的耦合变量[10]。
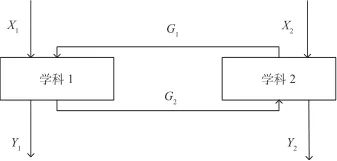
图1 两学科耦合关系[10]
Fig.1 Coupling relationship between two disciplines[10]
直接对耦合的多学科模型进行求解将消耗大量的计算资源,需要对模型进行解耦。对于无人机的气动隐身联合优化而言,一方面,无人机的外形同时影响着气动性能与隐身性能,例如圆形机身截面有利于减小浸润面积,降低空气阻力,但会造成电磁波从任意方向辐照出现较强的雷达回波,不利于隐身设计;又如飞翼布局在隐身性能上优于常规布局,但由于其缺失尾翼等结构,在气动性能上有所缺失。无人机外形是优化中的耦合变量。同时,气动隐身联合优化通过修改无人机外形进行气动与电磁特性分析来进行优化,无人机外形又作为优化中的输入变量。根据多学科耦合关系的处理方法,将耦合变量作为设计变量可以减少耦合关系带来的影响,无人机的外形作为设计输入变量,使得联合优化过程中针对气动性能与隐身性能的分析能够相对独立地进行。
图2给出了气动隐身联合优化的典型过程[11]。包括无人机初始外形的参数化建模,几何模型与计算网格生成,基于计算网格开展气动特性计算和电磁特性计算,随后评估目标函数和约束条件,如果不满足设计需求,则基于一定的原则生成新的几何外形,往复进行气动特性和隐身特性的计算,直至得到稳定收敛的优化结果。图中所展示的联合优化过程思路清晰,其中无人机外形参数化[12]、网格生成技术[13]以及优化建模与求解[14]均属于共性关键技术,对气动与隐身联合优化发挥着支撑性作用。
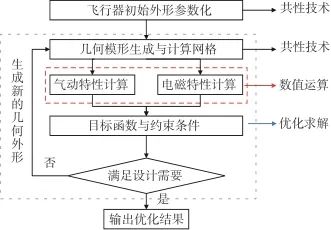
图2 气动隐身联合优化过程示意图
Fig.2 Schematic diagram of aerodynamic stealth joint optimization
值得注意的是,在目标函数与约束条件方面,常用升阻比、升力系数等无量纲量来表征气动性能,用雷达散射截面来表征隐身性能。但由于评估气动与隐身性能的参数单位与数量级不尽相同,在处理优化的目标函数时,需要对优化指标进行无量纲化处理,并保证气动与隐身的优化指标在同一量级。
气动特性计算和电磁特性计算均会带来巨大的计算量,尤其在数值精度要求更高的时候。气动与隐身联合优化的目标可以概括为以尽可能高的效率获得高可信度的优化结果。为了达成这一目标,潜在的技术路线包括:(1)通过工程算法提高联合优化效率,工程算法能够以更高的效率计算评估气动和隐身特性;(2)通过代理模型提高联合优化效率,在迭代过程中减少复杂费时的气动和隐身数值运算,用一个近似模型来表征设计量同气动和隐身特性之间的关系;(3)通过改善优化流程提高联合优化效率,通过引导优化或者借助梯度信息,改善优化算法及其求解流程,以更小的迭代次数完成高质量的求解。下面分别详细阐述。
2.1 采用工程算法提高气动/隐身特性评估的效率
在图2基础上,图3展示了工程算法参与优化的示意图。在数值运算方面,将计算量大的高精度气动和电磁特性计算替换为高效率的气动和电磁特性计算,以增加评估效率。
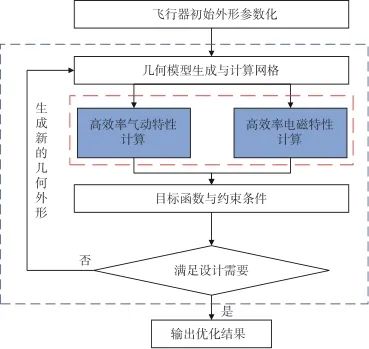
图3 工程算法参与优化示意图
Fig.3 Schematic diagram of optimization with engineering algorithms
针对气动计算,可以选择具有较高精度的工程算法如涡格法和面元法。涡格法[15]是在模拟物体的离散网格面上布置马蹄涡并形成涡格系统,计算涡格系统诱导的速度场在翼面上满足固体壁面速度无穿透边界条件,进而求解气动问题。面元法[16]通过将无人机表面离散为面元,在面元上布置点源、点汇、点涡和偶极子叠加得到任意几何外形的绕流流场。两种方法均基于势流理论,经过改进可以解决一系列亚跨超声速流动问题,计算精度有限,但能够在早期概念设计阶段实现优化选型。
对于电磁散射计算,也可以选择多类工程算法,几何光学法[17]描述电磁波在两种不同介质的分界面上的发射与折射;物理光学法[18]根据高频场的局部性原理完全忽略了目标各部分之间的相互影响,通过对感应场的近似积分求得散射场;几何绕射理论[19]是由已知简单问题的严格解发展而来的,通过解决边缘绕射问题弥补了几何光学法和物理光学法的不足;物理绕射理论[20]把散射场表示为物理光学贡献和边缘贡献之和,并利用二维尖劈问题的严格解来提取边缘贡献。这些方法均属于高频计算方法,使用条件为入射电磁波与目标之间满足电大尺寸关系,适用于在高频辐照条件下获得近似解。对于无人机未来可能采用的精细结构,如机翼后缘喷流装置、进气道唇口等,工程类算法往往难以满足联合优化精度要求。
2.2 采用代理模型提高气动/隐身特性评估的效率
为了避免在多次迭代中对新的无人机构型开展计算量庞大的数值分析,提出了基于代理模型的优化求解思路。代理模型方法由于能显著提高优化问题的求解效率,在航空航天领域得到了广泛应用,并逐步发展成为一类优化路线[21-22]。
代理模型的雏形是20世纪70年代发展的多项式响应面[23],经逐步发展形成了代理优化发展方向。代理优化的有效性很大程度上依赖于代理模型的近似精度,否则将无法保证得到可信赖的优化结果。随着飞机优化技术的蓬勃发展,代理模型的应用对象不断扩大,提高模型精度的方法也在不断涌现[24],如通过合理构造加点策略自适应提高模型精度。
图4给出了多项式代理模型的典型流程示意图。多项式代理模型使用简单的函数在整个设计空间内拟合目标函数和约束方程[23],由此简化了计算方法和数学模型。对应的构造可以分为两步:其一是试验设计(Design of Experiment,DOE)[24],以获得足够的响应量观测值,其二是利用回归技术[25]对试验结果进行拟合,得到一阶或者多阶代理模型的系数。
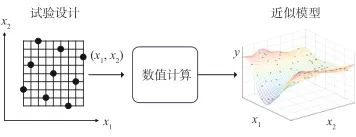
图4 多项式代理模型一般流程
Fig.4 General process of polynomial proxy model
多项式代理模型适合于处理低维问题。对于高维问题,可以通过增加多项式的次数来强化其描述复杂问题的能力,但存在过拟合的风险。
图5给出了基于代理模型开展气动与隐身联合优化的流程示意图,包括:
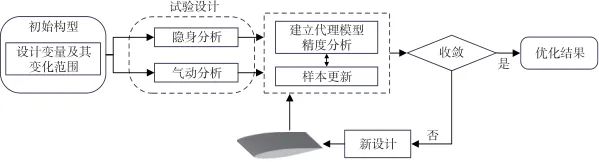
图5 基于代理模型开展气动隐身联合优化示意图
Fig.5 Schematic diagram of aerodynamic stealth joint optimization based on proxy model
(1)确定初始构型的设计变量及其变化范围。
(2)开展试验设计,采集样本点数据;基于样本点数据构建代理模型,并开展模型拟合精度分析。
(3)联立构建迭代优化流程并设置新设计产生方式,求解得到优化结果。
DOE是参数化建模与分析的重要手段,通过DOE可以研究各设计参数对无人机气动及隐身性能的影响。经典试验设计方法包括全因子[26]、中心组合[27]、D-优化[28]等,现代试验设计方法主要有拉丁超立方设计[29]、均匀设计[30]、正交设计[31]等。现代试验设计主要采用“空间填充”的思想,图6以二维空间中试验设计为例,给出了拉丁超立方设计和均匀设计选取样本点的差异[32-33]。样本点数据用于拟合输入与输出关系,不同的DOE选取方法会导致代理模型的近似精度不同。
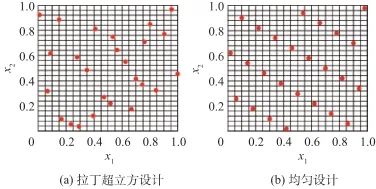
图6 不同的样本点选取方法对比[32-33]
Fig.6 Comparison of different sample point selection methods[32-33]
概括来讲,基于代理模型的气动与隐身联合优化的难点主要体现在:
(1)气动和电磁特性与无人机结构之间存在严重的非线性,人们期望采用适量的样本点获得高精度预测结果。这也是代理模型预测的共性难点。
(2)针对单学科优化的代理模型引入的误差在多目标联合评估中存在放大效应,影响联合优化结果的可信度,因此联合优化要求代理模型具有更高精度,这是气动与隐身联合优化面临的特殊难点。
为了克服上述两个难点,设计合理的代理模型加点策略是潜在的解决路径[34]。图7(a)展示了传统基于代理模型的优化流程,先选择样本点,构建代理模型并验证模型精度,进行优化搜索且在优化过程中保持代理模型不变。该策略的特点是流程简单,但如果原始样本点生成的代理模型精度差,有可能得到不可信的优化设计结果。
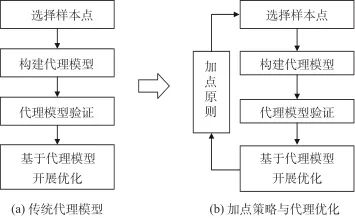
图7 代理优化及其改良
Fig.7 Proxy optimization and the related improvement
图7(b)所示考虑加点准则的代理优化是一种自适应方法。其机理是在优化过程中以一定方式选择新的构造样本并不断更新代理模型,最终提高代理模型预测精度。相应的典型加点准则包括改善期望准则[35]、改善概率准则[36]、置信下界准则[37]以及最小化代理模型预测准则[38]。与传统代理模型相比,自适应代理模型方法对应的优化周期得以延长,但该策略的设计结果对初始代理模型不存在较大依赖。
在加点策略的实施过程中,气动与隐身联合优化带来的新的挑战是:对于单目标优化,加点策略用于提高代理模型在最优解附近的精度,而气动与隐身联合优化的结果为一组Pareto最优解,为了保证优化结果的收敛性和多样性,要求加点策略提高代理模型在Pareto解集附近的精度。
代理模型选择方面,常见模型包括多项式代理模型、基于神经网络的代理模型[39]、Kriging模型[24]等。其中基于神经网络的代理模型是利用神经网络取代了多项式拟合,对应的计算精度更高。常见的基于神经网络的代理模型有基于径向基函数(Radial Basis Function,RBF)[40]的代理模型和最小二乘支持向量回归机代理模型[41]。Kriging模型是一种无偏估计模型,通过已知试验点信息来预测未知试验点。该模型假设数据之间满足正态分布,因此能够给出未知量的预估值以及预估值的误差估计。韩忠华在文献[24,42]中论述了Kriging模型的基本理论和算法,并以气动优化为例讨论了影响Kriging模型鲁棒性和效率的关键因素。
在不同代理模型的取舍方面,一般考虑的因素包括拟合精度、计算成本、数值噪声与复杂函数处置、对初始样本数量的要求等多个方面。
2.3 通过改善流程加速迭代寻优
优化问题由来已久,相关文献较多,在无人机设计与应用中更是应用广泛。优化设计的三要素,分别是优化算法选择、设计变量选择及范围设置、优化目标和约束条件设置[43]。无人机气动与隐身联合优化求解面临的主要挑战是在高维度设计变量和高可信度优化需求等约束条件下平衡资源开销与最优解引导。而改善优化流程的目的是以更高的效率获得优化结果或者以更大的概率获得全局最优解。图8为基于改善流程的联合优化示意图。优化举措包括但不限于选择更合适的优化算法在搜索空间设置正确的引导、通过分层和并行处理适应高维度设计变量以及在启发求解中置入智能方法加速优化迭代。
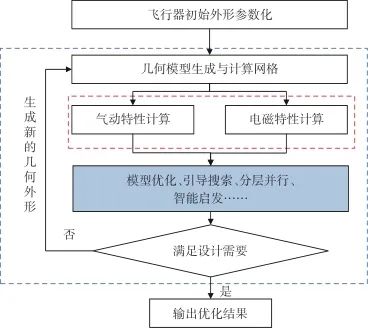
图8 改善优化流程示意图
Fig.8 Improvement and optimization process diagram
具体求解方面,联合优化求解可以分为基于非梯度信息和基于梯度信息两大类。非梯度类算法利用概率转移规则而不是确定性规则,理论上可以获得全局最优解。其典型代表是模拟退火算法、遗传算法、粒子群算法和免疫算法等进化类算法[44],具有不依赖数学模型处理复杂问题等优势。该类算法的难点在于如何建立具体优化问题(无人机气动隐身联合优化)同启发类模型的映射关联关系,以及结合收敛求解需求设置合理的搜索策略及迭代调控举措。
梯度类算法需要计算目标函数对设计变量的梯度,并基于梯度信息进行寻优[45],其核心是如何高效地获取准确的梯度信息以及选择合理的下降步长,以实现快速收敛。常见的获取梯度信息的方法包括有限差分法[46]、复数差分法[47]、自动微分法[48]以及伴随方程[49-50]等。四类方法逐步发展,相应的特点概括如图9所示。
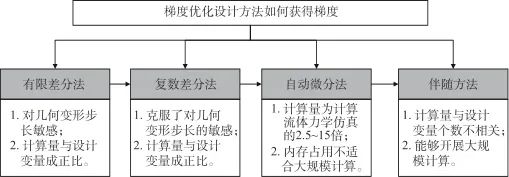
图9 几种不同的梯度获取方法
Fig.9 Several different gradient acquisition methods
通过求解伴随方程计算目标函数梯度的优势是该过程的计算量与设计变量个数无关。以气动优化为例,求解一次流场控制方程和其伴随方程即可得到目标函数关于所有设计变量的梯度。因而基于伴随方程的梯度优化可大幅提升优化效率。其基本流程如图10所示,注意此时一般采用如序列最小二乘算法[51-52]等适用于非线性约束的寻优算法,可以处理等式和不等式约束。
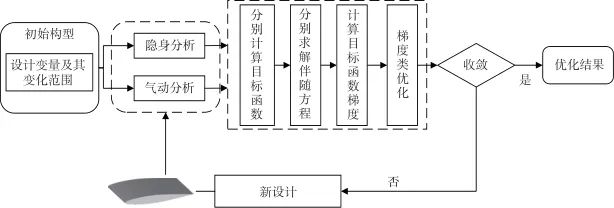
图10 基于伴随方程的气动隐身综合优化示意图
Fig.10 Aerodynamic stealth comprehensive optimization based on adjoint equations
当前,伴随方法在气动优化设计中已得到广泛应用,实现形式又分为连续伴随[53]和离散伴随[54]两种。两种方法存在形式上的不同,但基于同样的高质量网格求解出的梯度值是一致的。
3 气动与隐身优化的共性关键技术
图2所展示的气动与隐身联合优化过程中参数化建模、网格划分是基础性的,对获得高可信度的优化结果具有支撑性作用。这里对这几类关键技术进行总结梳理。
3.1 参数化建模
参数化建模是无人机气动、隐身或结构优化的基础。根据建模的维度,一般分为曲线建模和曲面建模[55]。
3.1.1 曲线建模
曲线建模可以分为两大类,一类是描述型参数化方法。它通过若干待定参数的数学方程对翼型曲线进行拟合,并通过调整参数以改变翼型曲线。PARSEC方法[56]、基于B-样条曲线与贝塞尔曲线的翼型描述法[57]、类别/形状函数变换方法[58]等属于这一类参数化方法。
另一类是几何变换翼型参数化方法,是在已有基准翼型上叠加基函数进而得到的新翼型。Hicks-Henne方法[59]是该类方法中的代表,它通过在原有翼型上叠加扰动函数得到。
3.1.2 曲面建模
曲面建模的直观形式是将剖面(曲线)建模结合线性插值技术、放样得到曲面,但如此处理得到的曲面精度较差。精细的曲面参数化建模可分为两大类,一类是直接建模方法;另一类是变形造型方法。
直接建模方法通过构造沿横向和纵向的两簇曲线直接张成参数化的曲面,如Bezier曲面[60]以及B-样条曲面[61]等。这里以Bezier曲线为例进行阐述,其表达式为
|
| (1) |
式中,
![]()
为控制点,
![]()
为m阶Bernstein多项式,
![]()
是归一化条件下横坐标。通过张量积形式实现由Bezier曲线到Bezier曲面的转换
|
| (2) |
式中,
![]()
、
![]()
分别为
![]()
方向上的基函数,
![]()
为控制顶点。式(1)~(2)对应的曲面构建方法可推广至非均匀有理B-样条曲面。非均匀有理B-样条曲面已经成为二维和三维作图软件最常用的方法之一,在确保曲面和曲线的连续性上表现优异。
变形造型方法是在已有曲面外形基础上做相应的变形从而得到新的曲面。该类方法的典型代表是自由曲面变形(Free Form Deformation, FFD)技术[62-63]。其原理是构造一个由三维控制点构成的包围待变形物体的长方体控制框架,改变控制框架的外形引导待变形物体产生相应的变形,并通过计算得到变形后物体的坐标。
图11展示了FFD参数化建模中的控制点、翼型的三维展示以及控制点引导示意。
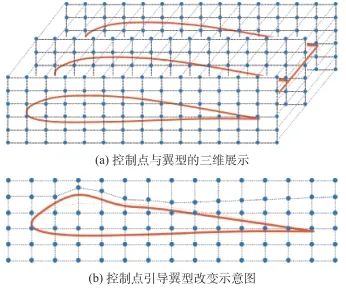
图11 FFD参数化建模的示意图[63]
Fig.11 Schematic diagram of FFD parametric modeling[63]
FFD算法能够同时控制几何和网格,减少参数化重建和网格重新剖分的工作量;具有应对复杂对象的通用性、局部变形的精细性以及曲线和曲面的连续光滑性。在曲线建模和曲面建模的基础上对无人机开展几何建模与参数化表征时,鉴于结构复杂性,一般需要分部件开展[64]。
3.2 网格技术
网格技术是开展气动数值计算和电磁散射计算的基础,由于气动计算和电磁散射计算的机理不同,对应的网格划分也有所区别。
3.2.1 气动力计算中的网格划分
结构化网格和非结构化网格[65]是两种气动计算中常用的网格方法,两者在生成方式、网格形状以及应用方面均有所不同:
(1)生成方式
结构化网格是由规则的网格单元(如矩形、正方形、立方体)按照一定的规律构成的网格,通常可以使用简单的算法生成。这种规则性和均匀性使得结构化网格可以通过简单的参数来控制网格的大小和密度,从而实现对网格的精细调节。
非结构化网格则是由不规则的网格单元(如三角形、四边形、四面体、六面体等)组成的网格,需要通过离散化方法、插值方法或优化算法来获得较好的网格质量,需要更复杂的算法和技术生成。
(2)网格形状和拓扑结构
结构化网格的网格单元形状和拓扑结构是规则的,例如二维情况下常见的矩形网格、三维情况下常见的六面体网格。而非结构化网格的网格单元形状和拓扑结构是不规则的,可以是不规则的多边形或多面体。
(3)灵活应用方面
直观地,非结构化网格具有更大的灵活性,可以根据几何形状的要求在关键位置灵活地调整网格密度。在实际工程应用中,几何模型通常较为复杂,复杂的几何模型对结构化网格划分技术要求较高,有可能导致结构化网格质量较低。
气动计算中需考虑研究目标周围的流场情况,需要建立一个外场模拟自然来流,一般需结合气动计算条件设置外场网格的边界。在具体实现方面,结构网格包括径向基函数法[66]、无限插值方法[67]、有限元方法[65]、弹性体方法[68]以及四元数方法[69]等,非结构网格亦有不同的实现方法,在具体应用中可根据具体问题对网格质量和生成过程鲁棒性的要求,选择合适的网格变形方法。
3.2.2 电磁特性计算中的网格划分
电磁散射计算方面,针对不同的电磁场求解方法,对应的网格划分策略有所不同。经过多年的发展,关于电磁场的典型数值求解方法包括时域有限差分算法(Finite Difference Time Domain,FDTD)[70]、有限元算法(Finite Element Method,FEM)[71]以及矩量法(Method of Moments,MoM)[72]。
FDTD离散的对象是时域微分形式的Maxwell方程组,所使用的离散形式是立方体网格,如图12(a)所示,网格划分相对简单,缺点是对精细结构的目标求解精度差。FEM算法基于频域Maxwell方程,其求解的对象是时谐电磁场,采用了拟合效果更好的四面体网格对求解区域进行剖分,求解精度得以提高,如图12(b)所示,适合于含有精细结构的目标电磁计算。MoM则基于一种完全不同的求解思路,它包含“格林函数”“源-场关系”“等效原理”三个支撑理论。在模型离散化方面,按照目标材料的特性可以分为两种情况,第一种是均匀介质,可以采用面等效原理,第二种是非均匀介质,可以采用体等效原理。当采用面等效原理时,要求对目标表面做网格划分且网格须为三角形网格,如图12(c)所示。
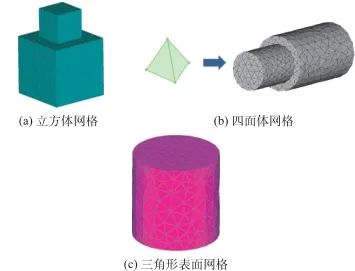
图12 不同电磁求解算法对应的网格划分方式
Fig.12 Different mesh methods according to electromagnetic calculation
3.2.3 气动力与电磁特性计算中网格划分的区别
理论上气动力和电磁特性计算中网格划分的目的是更好地逼近几何外形并精确求解波动方程。但在实际应用层面有所区别。
(1)网格大小的一致性有所不同
对于气动计算,往往需要在流场中大梯度区域内加密网格,如机翼前缘、翼身融合处、进气道口等区域,即网格大小随区域有所变化;对于电磁计算,网格大小一般是一致性的,比如网格大小在辐照电磁波波长的1/10或者1/16的量级,可满足计算要求[70]。
(2)网格形状的多样性有所不同
对于气动计算,网格类型粗分为结构网格和非结构网格,对应的种类较多,对于电磁计算,结合计算方法的不同,常用的网格包括六面体、四面体以及三角形面网格[72]。
4 不同技术路线的发展现状
4.1 基于工程算法的联合优化研究进展
早在1996年,张才文等[73]利用工程估算算法计算飞机气动力系数,并在高频区仅考虑菲涅尔区内电磁流对散射场的贡献,降低了气动和RCS计算工作量,建立了联合优化框架,开展了联合优化分析。2003年,高正红等[74-75]利用线化格林函数法与粘性修正相结合的方法求解气动特性,利用物理光学法与等效电流法相结合的方法求解电磁特性,并基于遗传算法开展气动与隐身综合优化。2006年,何开锋等[76]针对典型翼身组合体飞行器构型,分别采用面元法和物理光学法计算气动与雷达散射截面。2007年,Lee等[32-33]针对飞翼布局无人机,分别采用全速势方程和物理光学法对气动与隐身性能进行评估。
这一时期的工程算法精度较低,得到的气动与隐身联合优化结果仅提供参考价值,低精度优化设计的外形在实际应用中难以获得预期的性能[77],需要采用高精度计算模型方可获得性能优异的外形,这一需求也不断促使工程算法的计算精度逐步提高。具体来讲,气动计算逐步采用基于雷诺平均NS方程求解的方式,电磁散射计算逐步采用面元/边缘结合方法,其中面元散射场采用物理光学法计算,边缘的绕射场采用等效电磁流得到。
2009年,胡添元等[78]针对翼身融合布局飞行器,采用面元/边缘结合法计算RCS。2017年,夏露等[79]针对飞翼布局翼型无人机,采用基于雷诺平均NS方程求解的方法评估绕翼型流场;电磁散射计算方法同文献[78]一致。2017年,王荣等[80]针对双后掠飞翼布局的平面外形进行联合优化,气动特性分析采用求解雷诺平均NS方程的方法,使用格心有限体积法离散计算域,时间推进采用隐式处理方法大幅节省了计算时间。电磁散射计算方法同文献[78-79]相似。值得关注的是,2021年,张伟等[81]在评估翼型的RCS时,假设翼型为无限长,利用二维矩量法获得RCS,建立了有限长度翼型与无限长度翼型之间的联系,由此近似获得对应的三维翼型的RCS值,大幅节省了计算时间,但该方法的推广性有待验证。这一阶段的工程算法计算精度大为提高,得到的优化结果具有更好的参考性。
4.2 基于代理模型的联合优化研究进展
代理模型的选取方面,2006年,何开锋等[76]通过基于神经网络和模糊逻辑的响应面方法,实现了对翼身组合布局飞行器气动与隐身一体化优化。接着在2009年[82]以“小样本+Kriging代理模型的方式”得到联合优化解。2013年,张德虎等[83]构造了插值型和回归型两类代理模型,较为准确地预测了气动和隐身气动特性。2014年,张彬乾等[84]针对飞翼布局隐身翼型,构建了基于RBF神经网络的代理模型;邓海强等[85]针对翼身融合布局无人机,基于RBF神经网络法建立了设计参数与升阻比、机翼弯矩、干净构型俯仰力矩系数和RCS之间的代理模型,并以未配平状态升阻比最大、配平状态升阻比最大、配平状态升阻比尽量大和机翼弯矩尽量小为多目标函数,完成了不同目标引导下的翼身融合无人机外形优化设计。证实了RBF预测能力强、学习速度快和对连续非线性函数具有很强的一致逼近性等优势。
在代理模型加点策略方面,2016年,龙腾等[86]在径向基函数代理模型的基础上提出了自适应处理策略,通过增加样本点提高了模型在最优解附近的精度。2019年,朱新奇[55]针对飞机气动与隐身综合优化,整理得到了统一的代理模型形式,针对基于代理模型的单目标加点优化方法难以平衡局部和全局搜索的问题,提出了一种新的通用代理模型加点优化方法。樊华羽等[87]基于动态Kriging代理模型与期望改善加点策略,以及粒子群优化算法进行寻优设计,获得了Pareto前沿解。上述工作证实了将代理模型与加点策略相结合,能够有效促进代理模型在Pareto前沿附近的评估精度。
此外,在优化过程中自适应地改善外形描述能力引起了同行重视,2020年,张伟等[88]提出一种适用于代理模型优化的自适应参数化方法,利用基本效应法进行全局敏感性分析,得到设计空间关于目标函数的敏感区域信息。随后再对设计空间的敏感区域扩展设计纬度,能够更为自适应地精确描述翼型外形。
另一个值得关注的研究现象是,大多数的气动与隐身联合优化对象是飞翼布局无人机, Zia等[89]在2023年针对常规布局有人机开展了基于高斯过程代理模型的气动与隐身联合优化研究,并基于多目标遗传算法获得了优化构型,提升了气动和隐身性能。
深入的研究表明复杂约束条件会导致设计空间可行域呈现不连续的特征,且理想解大多靠近约束边界,这时传统代理模型的效能受到限制。与人工智能相结合的代理模型优化设计方法逐步得到重视[90-91]。
4.3 基于改善优化流程的联合优化研究进展
2006年,悉尼大学Lee等[32]针对飞翼布局无人机,提出了分层异步并行启发式算法,能够以较快的速度迭代收敛得到优化结果。图13展示了基于该算法得到的一组Pareto最优解集对应的部分优化构型俯视图。图中M1~M15为Pareto最优解集,黑色框线代表初始构型。可以看出相对于初始构型,Pareto最优解级的长宽比、根部的锥度比和翼尖的锥度比均有增加。这样的变化使得气动与隐身性能得到了提升,Lee在文献中对比分析了优化构型M1、M2与初始构型的RCS与升阻比,M1、M2的RCS分别缩减了25%与11%,而升阻比提升了两倍。
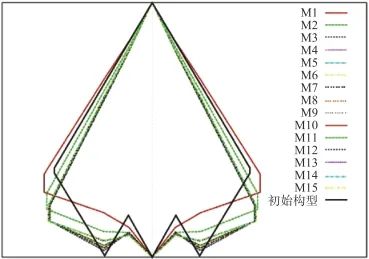
图13 优化结果展示[32]
Fig.13 Display of different optimization results[32]
2017年,夏露等[79]针对飞翼布局无人机使用分层交换差分粒子群算法进行优化避免了优化结果陷入局部最优。2018年,Karakoç等[92]使用多目标遗传优化方法对MULDICON布局无人机开展气动与隐身联合优化设计,表明启发式算法在气动与隐身联合寻优中具有流程简单、参数简洁的特点,能够达到迅速收敛的效果。
2019年,朱新奇[55]开展了有偏好引导的联合优化建模与求解。提出了一种可以考虑偏好倾向的多目标优化算法。该算法利用参考点表达偏好信息,使用子种群对参考点对应的偏好区域进行搜索,在相同计算量下实现了对整个Pareto前缘的更优搜索,是启发式算法与偏好选择相结合引导进化方向的有效举措。
在优化算法方面更深入的探索是在2023年王培君等[93]提出了自适应超参数基于分解算法的多目标进化算法,在翼型的气动与隐身联合优化中展现出较好的鲁棒性,并开展了与带精英策略的快速非支配排序遗传算法、不同配置下基于分解算法的多目标进化算法的对比,证实了该算法在最优收敛和收敛速度上均占据优势。
基于梯度的优化算法利用梯度信息寻找有利的搜索方向,但也容易陷入局部最优,对初始点的选择较为依赖。伴随方法的提出一定程度上解决了“维数灾难”问题。该方面的联合优化主要进展包括:
2019年,陈保等[94]开展了多项基于伴随方法的气动隐身优化设计研究,其中气动特性评估分析中梯度信息通过求解伴随方程得到,该方面方法已经比较成熟。电磁特性分析中梯度信息的获取则是通过TAPENADE工具对物理光学法程序进行微分处理得到。随后2020年,周琳等[95]提出了求解麦克斯韦方程组离散伴随方程获得梯度信息的方法,为精确高效获得电磁特性梯度信息提供了理论基础。2021年,Li等[96]考虑不同电磁散射计算方法如矩量法、多层快速多极子算法、物理光学法在不同频段下的精度,通过求解相应的伴随方程得到隐身目标特性关于设计变量的梯度。2023年,黄江涛等[97]在三维矩量法的基础上进一步推导了麦克斯韦方程的离散伴随方程,并使用多层快速多极子方法予以快速求解,获得目标RCS的梯度信息。上述进展揭示了电磁特性评估中梯度信息获取技术的进步。图14展示了联合优化前后气动特性的改善情况。可以观察到,优化外形的上表面激波强度明显低于初始外形,接近无激波状态。这一现象在外翼段前半部分尤为明显。
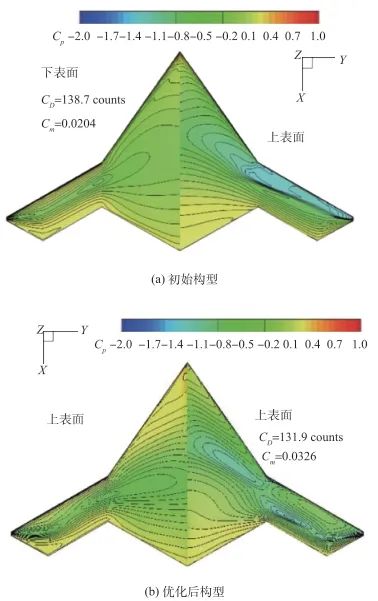
图14 优化结果对比[97]
Fig.14 Comparison of optimization results[97]
5 结束语
5.1 开展基于知识提取-指标驱动的隐身无人机总体设计
当前的优化应用,大多针对构型相对简单的飞翼无人机。在先进无人机设计过程中,总体设计与布局设计占据着支配地位,不仅绝大程度上影响无人机综合气动与隐身性能,更决定了气动与隐身联合优化中无人机初始参数的设定与优化范围的选取。对无人机设计的历史数据分层级建立“宏观需求-设计规则-布局构型”“细化指标-典型案例-性能空间”等不同颗粒度的关联关系,形成能够有效表达无人机概念设计的知识库并支持有效推理,实现无人机总体设计的智能辅助,能够解决无人机复杂设计过程中关联耦合和知识共享问题,减小总体设计域。
5.2 利用人工智能方法提升气动与隐身性能评估效益
气动及隐身特性与无人机外形设计变量之间强烈的非线性关系导致传统的代理模型评估效益受限。基于深度学习网络的代理模型能够针对高维度设计变量实现高度拟合,基于小样本的学习方法能够降低代理模型训练对标记样本的依赖。此外,基于现有人工智能方法在图像处理与识别方面的发展基础,针对无人机的流场图像以及逆合成孔径雷达成像图像的学习,有望通过智能方法实现对不同无人机气动特性和隐身特性的快速准确评估,具有很大的应用潜力。
5.3 开展气动与电磁计算网格的一致性应用
文中第3节分析了气动计算和电磁计算对网格的要求以及两者的区别,在现有的应用中,单一学科分析对网格的设计是出于该学科范畴内计算精度和计算效率,对于同一个几何模型分别进行气动网格和电磁网格剖分,再对两套网格开展气动和电磁散射性能评估,网格划分的差异所引入的误差将不可避免地导致气动和隐身计算并非针对同一对象,尤其针对具有精细结构的无人机外形。因此在开展气动隐身联合优化过程中,保持优化对象的一致性十分重要,一种潜在的技术手段是对优化对象生成一套兼顾气动和电磁特性计算特点的网格并开展一致性数值分析。
5.4 针对现有无人机开展隐身强化设计与实现
为提高无人机在对抗环境中的生存概率和突防能力,对现有无人机进行隐身增强设计具有广阔的应用空间。隐身增强设计的内涵包括对无人机气动性能与隐身性能的快速精确评估;强散射源的筛选和形成机理分析;高效率精确代理模型的构建;以及针对强散射源的气动与隐身联合优化。隐身增强设计需有明确的指标牵引,其理论基础是气动与隐身联合优化,具体举措在于对形成强散射源的无人机局部区域开展联合优化。























 1082
1082

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








