MR chapter 2 Configuration Space

好悬给我拽开线

已于 2023-08-29 15:06:32 修改

阅读量439

点赞数

分类专栏： Modern Robotics阅读文章标签： mr

于 2023-08-29 10:17:37 首次发布

本文链接：https://blog.csdn.net/qq_33673253/article/details/132182174

版权

Modern Robotics阅读专栏收录该内容

5 篇文章

订阅专栏

机器人是通过使用各种类型的joints将一组称为links的bodies相互连接来机械构建的。

本书中考虑的所有机器人都有可以建模为刚体的链接links。

the robot's configuration: a specification of the positions of all points of the robot.

由于机器人的链接是刚性的，并且已知形状，因此只需要几个数字来表示其配置 configuration。

例如，门的配置可以由单个数字表示，即其铰链的角度 θ。

机器人的自由度 degrees of freedom ((dof) 的数量是表示其配置所需的实值坐标的最小数量。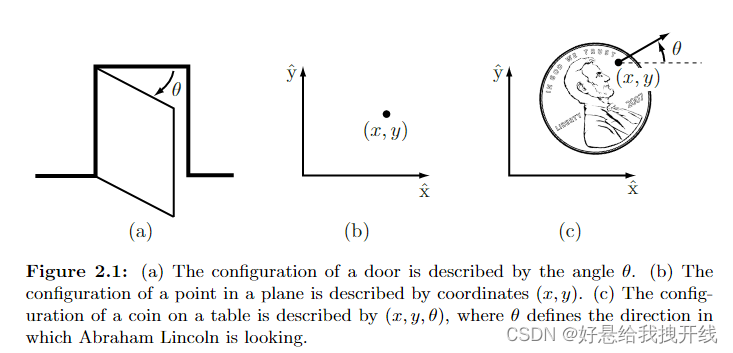

定义：

包含机器人所有可能配置的 n 维空间称为配置空间 (C-space)。

在本章中，我们研究了一般机器人的c空间和自由度。由于我们的机器人是由刚性连杆构造的，我们首先检查单个刚体的自由度，然后检查一般多连杆机器人的自由度。

接下来我们研究 C 空间的形状shape（或拓扑topology）和几何及其数学表示mathematical representation。本章最后讨论了机器人末端执行器的 C 空间，即任务空间task space.。在本章中，我们将更详细地研究单个刚体的 C 空间的数学表示。

2.1 Degrees of Freedom of a Rigid Body 单刚体自由度

我们已经应用以下通用规则来确定系统的自由度数量：

空间刚体 spatial rigid body 有六个自由度。平面刚体 planar rigid body 有三自由度。也可以通过将平面刚体视为具有六个自由度的空间刚体来获得，但具有三个独立的约束 zA = zB =zC = 0。

2.2 Degrees of Freedom of a Robot

这一观察提出了一个公式来确定机器人自由度，只需数刚体和关节的数量。

在本节中，我们精确地推导derive出这样的公式，称为Gr ̈ubler's formula,确定平面机器人和空间机器人的自由度数。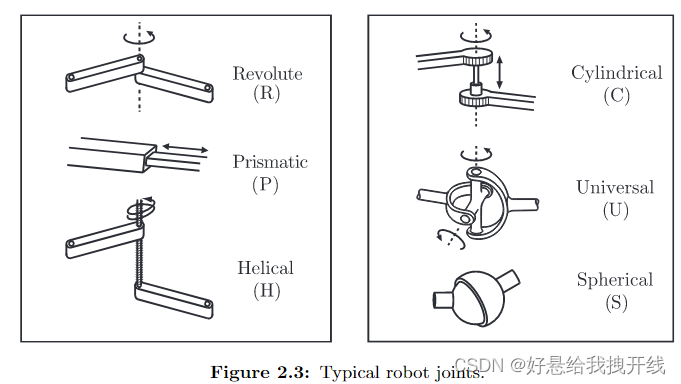

helical螺旋形

2.2.1 Robot Joints

RPH都有一个自由度。

revolute joint (R), also called a hinge joint

e prismatic joint (P), also called a sliding or linear joint

The helical joint (H), also called a screw joint

CU具有两个自由度 S有3个

The spherical joint (S), also called a ball-and-socket joint

2.2.2 Gr ̈ubler's Formula

可以使用 Gr̈ubler 公式计算具有链接和关节的机构的自由度数

命题Proposition 2.2.：

考虑一个由 N 个links组成的机构mechanism，其中地面ground也被视为链接link。设J为关节数，m为刚体自由度数(平面m = 3，空间m = 6)。fi 是关节 i 提供的自由度数，ci 是关节 i 提供的约束数，其中所有 i 的 fi + ci = m。公式为：

只有当所有关节约束都是独立的时，这个公式才成立。如果它们不是独立的，则公式提供了自由度数量的下限lower bound。

我们区分两种类型的mechanism：开放链open-chain mechanisms（也称为serial mechanisms）和封闭链closed-chain mechanisms。

A closed-chain mechanism is any mechanism that has a closed loop.

A person standing with both feet on the ground is an example of a closed-chain mechanism, since a closed loop can be traced from the ground, through the right leg, through the waist, through the left leg, and back to ground (recall that the ground itself is a link).

An open-chain mechanism is any mechanism without a closed loop; an example is your arm when your hand is allowed to move freely in space.

例Example 2.3（(Four-bar linkage 四连杆 and slider–crank mechanism 滑块曲柄）

图2.4(a)所示的平面四杆连杆机构由四个连杆(其中一个接地)组成，排列在一个闭环中，并通过四个转动关节连接。由于所有链接都被限制在同一个平面上，我们有 m = 3。N = 4, J = 4，fi = 1, i = 1,。, 4 代入Subsituting Gr̈ubler 的公式，我们看到四杆连杆机构有一个自由度。

图2.4(b)的滑块曲柄闭链机构可以通过两种方式进行分析:(i)该机制由三个转动关节和一个棱柱关节(J = 4，每个fi = 1)和四个连杆(N = 4，包括地面连杆)组成

(ii)该机制由两个转动关节(fi = 1)和一个RP关节组成(RP关节是转动关节和棱柱关节的串联，使fi = 2)和三个连杆(N = 3;记住，每个关节精确地连接两个物体)。

在这两种情况下，该机制都有一个自由度。

例Example 2.4 （一些经典的平面机构）

图2.5(a)中转动关节的k-link平面串行链(称为a kR robot for its k revolute joints)有N = k + 1个连杆(k个连杆加地面)，J = k个关节，并且fi = 1 对于所有 i，有

$dof = 3((k+1)-1-k)+k=k$

Example 2.5(A planar mechanism with overlapping joints重叠关节)

The planar mechanism illustrated in Figure 2.6 has three links that meet at a single point on the right of the large link.

回想一下，根据定义，关节恰好连接两个链接，交点处的关节不应被视为单个转动关节。

相反，它被正确解释为两个相互重叠的旋转关节。

使用 Gr̈ubler 公式推导出该机制的自由度数有多种方法

该机制由八个链接（N = 8）、八个转动关节和一个棱柱关节组成
或者，右下角的旋转-棱柱关节对可以看作是一个双自由度关节，看作一个构件在这种情况下，链接数为 N = 7，具有七个旋转关节，以及单个双自由度旋转-棱柱对。
- $dof = 3(7 -1-8)+7(1)+1(2)=3$

Example 2.6(Redundant constraints and singularities)（冗余约束和奇点）

Redundant ：对于图2.7(a)的平行四边形连杆parallelogram linkage，N = 5, J = 6, and fi = 1 for each joint.公式计算自由度为0。具有零自由度的机制根据定义是刚性结构。然而，从检查该图可以清楚地看出，该机制实际上可以以1自由度移动。事实上，三个平行链接中的任何一个及其两个关节都对机制的运动没有影响。换句话说，正如 Gr̈ubler 公式所要求的那样，关节提供的约束并不独立。

singularities：图 2.7(b) 的平面五连杆也有类似的情况。接到地面的两个关节以一定的固定角度锁定，然后五杆连杆应成为刚性结构。然而，如果两个中间连杆的长度相同，相互重叠，那么这些重叠的link可以自由旋转两个重叠的关节。五连杆长度需要满足特定的配置才会出现这样的情况。此外，请注意，如果位置锁定了一对不同的关节，该机制确实成为预期的刚性结构

第7章讨论了封闭链中出现的构型空间奇点。

Example 2.7 (Delta robot）

图2.8中的德尔塔机器人由两个平台组成——下部一个移动平台，上部一个固定平台——由三条腿连接。每条腿包含一个平行四边形闭合链，由三个旋转关节、四个球形关节和五个连杆组成。加上两个平台，共有N=17个连杆和J=21个关节（9个旋转关节和12个球形关节）。根据Grüubler公式：dof = 6(17 − 1 − 21) + 9(1) + 12(3) = 15.然而，在这15个自由度中，只有三个在移动平台的末端效应器处可见。事实上，平行四边形腿的设计确保了移动平台始终与固定平台保持平行，从而使德尔塔机器人充当x–y–z笛卡尔定位装置x–y–z Cartesian positioning device。

其他12个内部自由度由平行四边形中的12个连杆（三个腿中的每一个在其平行四边形上具有四个连杆）绕其长轴的扭转来说明。（我的理解是表现为平行四边形连杆的自由度，只有三个表现在机构末端）

Example 2.8(Stewart–Gough platform)

Stewart-Gough 平台由两个平台组成，移动平台由六个universal–prismatic–spherical (UPS) legs连接。链接总数为 14 (N = 14)。六个universal关节(每个关节有两个自由度，fi = 2)，六个棱柱关节(每个关节都有一个自由度，fi = 1)和六个球形关节(每个关节有三个自由度，fi = 3)。关节总数为18个。将这些值代入m = 6的Gr̈ubler公式得到 dof = 6(14 − 1 − 18) + 6(1) + 6(2) + 6(3) = 6.

在Stewart–Gough平台的某些版本中，六个万向节被球形接头取代。根据Grüubler公式，该机构具有12个自由度；用球形关节代替每个万向节为每个腿带来了额外的自由度，允许绕腿轴进行扭转旋转。然而，请注意，这种扭转旋转对移动平台的运动没有影响。

Stewart–Gough平台是汽车和飞机驾驶舱模拟器的热门选择，因为该平台具有刚体的全部六个运动自由度。一方面，平行结构意味着每个腿只需要支撑有效载荷重量的一小部分。另一方面，这种结构还限制了平台相对于六自由度开放链末端执行器的运动范围的平移和旋转运动范围。

2.3 Configuration Space: Topology and Representation 配置空间：拓扑和表示

2.3.1 Configuration Space Topology 配置空间拓扑

到目前为止，我们一直在关注机器人C空间的一个重要方面——它的尺寸或自由度的数量。然而，空间的形状shape也很重要。

考虑一个点在球体表面上移动。点的C空间是二维的，因为配置可以用纬度和经度这两个坐标来描述。作为另一个例子，在平面上移动的点也有二维C空间，坐标为（x，y）。虽然平面和球体表面都是二维的，但很明显，它们的形状并不相同——当球体环绕时，平面无限延伸。（相同纬度但是两种不同的拓扑）

小球、大球和足球的二维表面都有相同的形状，这与平面的形状不同，这一观点通过表面的拓扑结构 topology of the surfaces 来表达。

如果一个空间可以在不切割或粘合cutting or gluing 的情况下连续变形为另一个空间，那么两个空间在拓扑上是等价的 topologically equivalent

球体可以简单地通过拉伸变形为足球，而无需切割或粘合，因此这两个空间在拓扑上9是等效的。但是，如果不切割球体，就无法将其转化为平面，因此球体和平面在拓扑上并不等效

一维拓扑空间包括圆、直线和直线的闭合区间 the circle, the line, and a closed interval of the line

圆在数学上被写成S或 $S^1$ ，一个一维的“球体”

线可以写成E或 $\mathbb{E}^1$ ，表示一维欧几里得（或“平面”）空间

由于 $\mathbb{E}^1$ 中的一个点通常由实数表示（在选择原点和长度刻度后），因此它通常被写成R或 $\mathbb{R}^1$ 。

包含其端点的线的闭合区间可以写成 $[a,b]\subset \mathbb{R}^1$

开区间[a,b]不包括端点a和b，在拓扑上等价于一条线，因为开区间可以拉伸为一条线。如图2.9所示。闭合区间在拓扑上不等同于直线，因为直线不包含端点。

在高维中，Rn是n维欧几里得空间the n-dimensional Euclidean space，Sn是（n+1）维空间中球体的n维表面。

例如，S2是球体在三维空间中的二维表面。

注意，空间的拓扑结构是空间本身的一个基本性质，与我们如何选择坐标来表示空间中的点无关independent。

一些C空间(配置空间 configration space )可以表示为两个或多个低维空间的笛卡尔乘积 Cartesian product；也就是说，这种C空间中的点可以表示为低维空间中点的表示的并集。例如：

平面中刚体的C空间可以写成R2×S1,因为该configuration可以表示为R2的坐标（x，y）和S1的角度θ的级联 concatenation。
PR机械臂的C空间可以写成R1×S1；在表达C空间的拓扑结构时，我们偶尔会忽略关节极限，即关节行程the travel of the joints 的边界；对于关节极限，C空间是线的两个闭合区间的笛卡尔乘积。
2R机械臂的C空间可以写成S1×S1=T2，Tn是（n+1）维空间中环面的n维表面；注意，S1×S1×··×S1等于Tn，而不是Sn；例如球面S2在拓扑上不等价于环面T2。
带有2R机械臂的平面刚体（例如移动机器人的底盘）的C空间可以写成 $\mathbb{R}^2 \times S^1 \times T^2= \mathbb{R}^2 \times T^3$
正如我们在第2.1节中所看到的，当我们计算三维刚体的自由度时，刚体的构型可以用R3中的一个点，加上二维球体S2上的一个点，加上一维圆S1上的一点来描述；得到的总C空间为R3×S2×S1

spherical pendulum 球面摆 rotating sliding knob 旋转滑动旋钮

2.3.2 Configuration Space Representation

重要的是要记住，空间的表示涉及一种选择（不唯一），因此它不像空间的拓扑那样基本，拓扑是与表示无关

同一个点根据参考系的选择，三维空间可以有不同的坐标表示，以及长度尺度的选择，但无论这些选择如何，底层空间的拓扑结构都是相同的。

虽然在欧几里得空间中选择参考系和长度比例并使用向量来表示点是很自然的，但在曲面空间（如球体）上表示点则不那么明显。

选择n个坐标或参数来表示n维空间称为空间的显式参数化explicit parametrization。这种显式参数化对于特定范围的参数是有效的。

如果你在北极(纬度等于90◦)或南极(纬度等于- 90◦)附近行走，球体的经纬度表示是不令人满意的，在那里采取非常小的一步可能导致坐标的大变化。

北极和南极是representation的奇点，奇点的存在是球体与平面拓扑结构不同的结果。这些奇点的位置与球体本身无关，球体在任何地方看起来都是一样的，一切都与它所选择的表示有关。

当将速度表示为坐标的时间变化率时，参数化的奇异性尤其有问题，因为即使球体上的点以恒定速度移动，这些表示在奇点附近也可能趋于无穷大

如果您可以假设配置从未接近表示的奇点，那么您可以忽略这个问题。如果你不能做出这个假设，有两种方法可以克服这个问题：

在空间上使用多个坐标图coordinate chart，其中每个坐标图都是一个明确的参数化，仅覆盖空间的一部分，因此在每个坐标图中都没有奇异性。当配置表示接近一个图表中的奇点时，例如北极或南极，您只需切换到另一个图表，其中北极和南极远离奇点。如果我们定义了一组相互重叠的无奇点坐标图，并覆盖整个空间，如上面的两个图表，图表被称为形成空间图集 an atlas of the space 优点是表示总是使用最少的数 the minimum number of numbers 。缺点是在坐标图之间切换表示以避免奇点所需的额外簿记。（请注意，欧几里得空间可以由没有奇点的单个坐标图 coordinate chart 覆盖。）
使用隐式表示 implicit representation 而不是显式参数化。
- 隐式表示将 n 维空间视为嵌入在 n 以上个维度的欧几里得空间中，就像二维单位球可以被视为嵌入在三维欧氏空间中的曲面。
- 隐式表示使用高维空间的坐标（例如，三维空间中的（x，y，z）），但使这些坐标受到减少自由度的约束（例如，单位球体的x2+y2+z2=1）。
- 这种方法的一个缺点是，表示的数量比自由度的数量多。
- 一个优点是表示中没有奇点——在球体周围平滑移动的点由平滑变化的（x，y，z）表示，单个表示representation用于整个球体；不需要多个坐标图
- 另一个优点是，虽然为闭链机构closed-chain mechanism构建显式参数化或图谱可能非常困难，但很容易找到隐式表示：受定义闭环的闭环方程loop-closure equations约束的所有关节坐标joint coordinates的集合

特别是，我们使用九个数字，受六个约束，来表示刚体在空间中的三个定向自由度。这被称为旋转矩阵。除了无奇异性（与滚转-俯仰-偏航角等三参数表示不同），旋转矩阵表示还允许我们使用线性代数进行计算，如旋转刚体或改变表示刚体方向的参考系。

（滚转-俯仰-偏航角和欧拉角使用旋转空间S2×S1的三个参数（两个用于S2，一个用于S1），因此受到上述奇点的影响）

（另一种无奇异性的方向隐式表示，即单位四元数，只使用四个数字，受4维向量为单位长度的约束。事实上，这种表示是方向集the set of orientations的双重覆盖：对于每个方向，都有两个单位四元数。）

总之，许多C空间的非欧几里得形状促使我们在整本书中使用C空间的隐式表示。

2.4 Configuration and Velocity Constraints

对于包含一个或多个闭环的机器人，通常隐式表示比显式参数化更容易获得。

例如，考虑图2.10中具有一个自由度的平面四连杆机构。

四个环节总是形成一个闭环的事实可以用以下三个方程来表示：

这些方程是通过将四连杆机构视为具有四个旋转关节的串联链而获得的，其中

连杆L4的尖端总是与原点重合
L4的方向始终是水平的

这些方程有时被称为闭环方程loop-closure equations。对于四杆机构，它们由一组三个方程在四个未知数中给出。所有解的集合在四维联合空间中形成一维曲线，并构成C空间。

（在这本书中，当向量用于线性代数计算时，它们被视为列向量，例如，p=[1 2 3]T。然而，当计算不迫在眉睫时，我们通常将向量简单地视为变量的有序列表，例如，p=（1，2，3）。）

因此，对于包含一个或多个闭环的一般机器人，位形空间可以隐式地表示为列向量θ = [θ1···θn]T∈Rn和如下形式的闭环方程：

k≤n的一组k个独立方程。

这样的约束被称为完整约束 holonomic constraints，它们降低了c空间的维数。

holonomic 与 nonholonomic 的本质区别是什么？ - 知乎

（将刚体视为点的集合，点之间的距离约束可以被视为完整约束。）

c空间可以看作是嵌入在Rn中的n - k维的曲面(假设所有约束都是独立的)

设闭环方程为

$g(\theta)=0,g:\mathbb{R}^n\rightarrow \mathbb{R}^k$

的闭链机器人沿着时间轨迹θ(t)运动。两边对g(θ(t)) = 0对t求导，我们得到

可写作

$\frac{\partial g}{\partial\theta}(\theta)\dot{\theta}\quad=\quad0,\partial g(\theta)/\partial\theta\in\mathbb{R}^{k\times n},\mathrm{~and~}\theta,\dot{\theta}\in\mathbb{R}^{n}.$

该约束可写作： $A(\theta)\dot{\theta}=0,$

这种形式的速度约束称为pfaffian约束 Pfaffian constraints.

对于A(θ) =∂g(θ)/∂θ的情况，可以将g(θ)视为A(θ)的“积分”;

出于这个原因，形式 g(θ) = 0 的完整约束也称为可积约束 integrable constraints $r\dot{\theta}$

其所表达的速度约束可以被积分从而提供等效的配置上的约束 equivalent configuration constraints

我们现在考虑另一类与完整类型the holonomic type.完全不同的 Pfaffian 约束。考虑一个在平面上滚动半径为r的直立硬币，如图2.11所示。

硬币的配置由平面上的接触点(x, y)、转向角 steering angle φ和旋转角θ给出。因此，硬币的 C 空间是 $\mathbb{R}^{2}\times T^{2}$ ，其中 $T^{2}$ 是由角度 φ 和 θ 参数化的二维环面（ $S^{1}\times S^{1}$ ）。

硬币必须始终以 (cos φ, sin φ) 表示的方向滚动，前进速度 $r\dot{\theta}$ ：

$\left[\begin{array}{c}\dot{x}\\\dot{y}\end{array}\right]=r\dot{\theta}\left[\begin{array}{c}\cos\phi\\\sin\phi\end{array}\right].\quad(2.9)$

将四个c空间坐标收集到一个向量中

$q=[q_1~q_2~q_3~q_4]^\mathrm{T}=[x~y~\phi~\theta]^{\mathrm{T}}\in\mathbb{R}^{2}\times T^{2},$

上述无滑移滚动约束可以用以下形式表示

$\left[\begin{array}{cccc}1&0&0&-r\cos q_3\\0&1&0&-r\sin q_3\end{array}\right]\dot{q}=0.\quad(2.10)$

这些是 Pfaffian 约束的形式 $A(q)\dot{q}=0,A(q)\in\mathbb{R}^{2\times4}.$

这些约束是不可积的;也就是说，对于(2.10)中给出的A(q)，不存在可微函数g R4→R2，使得∂g(q)/∂q =A(q)

如果情况并非如此，则必须存在一个满足以下四个等式的可微 g1(q)：

$\begin{matrix}\partial g_1/\partial q_1&=&1&\longrightarrow&g_1(q)=q_1+h_1(q_2,q_3,q_4)\\\partial g_1/\partial q_2&=&0&\longrightarrow&g_1(q)=h_3(q_1,q_2,q_4)\\\partial g_1/\partial q_3&=&0&\longrightarrow&g_1(q)=h_3(q_1,q_2,q_4)\\\partial g_1/\partial q_4&=&-r\cos q_3&\longrightarrow&g_1(q)=-rq_4\cos q_3+h_4(q_1,q_2,q_3),\end{matrix}$

通过检查，应该清楚不存在这样的 g1(q)。类似地，可以证明 g2(q) 不存在，因此约束 (2.10) 是不可积的。（这些等式没法同时满足）

不可积的Pfaffian约束称为非完整约束 nonholonomic constraint。

这些约束降低了系统可行速度的维度dimension of the feasible velocities，但不会降低可达的 C 空间的维度。滚动硬币可以在其四维c空间中到达任何点，尽管它的速度有两个约束。

在第13章的轮式移动机器人研究中，我们更详细地研究了非完整约束。

2.5 Task Space and Workspace

我们现在介绍两个与机器人配置有关的概念：任务空间和工作空间。两者都与机器人末端效应器the configuration of the end effector 的配置有关，而不是与整个机器人的配置有关。

任务空间是机器人任务可以自然表达的空间。例如，如果机器人的任务是用笔在一张纸上绘图，那么任务空间将是 $\mathbb{R}^{2}$ 。

如果任务是操纵刚体，自然的任务空间的表示是刚体的C空间，表示连接到机器人末端执行器的坐标系的位置和方向position and orientation 。这是任务空间的默认表示形式。如何定义任务空间的决定是由任务驱动的，与机器人无关。

工作空间workspace是机器人末端执行器可以到达的配置规范。工作空间的定义主要由机器人的结构驱动，与任务无关。

任务空间和工作空间都涉及用户的选择；特别地，用户可以决定不需要表示末端执行器的一些自由度（例如，其定向）。

任务空间和工作空间与机器人的C空间不同。任务空间或工作空间中的一个点可以通过多个机器人配置来实现，这意味着该点不是机器人配置的完整规范not a full specification of the robot's configuration（理解为该点并不能完全确定机器人的全部配置即 full specification ）例如，对于具有七个关节的开链机器人，其末端执行器的六自由度位置和方向并不能完全指定机器人的配置。

任务空间中的一些点可能根本无法被机器人到达，例如黑板上的一些点。然而，根据定义，工作空间中的所有点都可以通过机器人的至少一种配置到达。

具有不同C空间的两个机构可能具有相同的工作空间。例如，考虑到末端执行器是机器人的笛卡尔尖端（例如，绘图笔的位置）并忽略方向；具有等长链节的平面2R开放链（图2.12（a））和具有等长链节的平面3R开放链尽管具有不同的C空间，但具有相同的工作空间。
具有相同C空间的两个机构也可能具有不同的工作空间。例如，将末端执行器作为机器人的笛卡尔尖端，忽略方向，图2.12（a）中的2R开放链将平面圆盘作为其工作空间，而图2.12（c）中的2L开放链则将球体表面作为其工作场所。

将坐标系连接到图2.12（d）的3R开链“手腕”机构的工具尖端，我们可以看到，该坐标系可以通过旋转关节来实现任何方向，但尖端的笛卡尔位置始终是固定的。这可以通过注意三个关节轴始终在尖端相交来看出。

对于这种机构，我们可能会将工作空间定义为坐标系方向的三自由度空间，S2×S1，这与该3R机构的C空间T3不同。

任务空间取决于任务；如果任务是指向激光指示器，那么围绕激光束的轴的旋转是无关紧要的，并且任务空间将是S2，即激光可以指向的一组方向。

Example 2.9.

图2.13的SCARA机器人是一种RRRP开放链，广泛用于桌面拾取和放置任务。

末端执行器配置完全由四个参数（x，y，z，φ）描述，其中（x，y，z）表示末端执行器中心点的笛卡尔位置，φ表示末端执行机构在x–y平面中的方向。

它的任务空间通常定义为R3×S1，它的工作空间通常被定义为（x，y，z）笛卡尔空间中的可达点，因为所有方向φ∈S1都可以在所有可达点上实现。

Example 2.10.

标准6R工业机械手可适用于喷涂应用，如图2.14所示。喷漆喷嘴连接到尖端可视为末端执行器。对任务来说重要的是喷嘴的笛卡尔位置，以及喷嘴指向的方向；围绕喷嘴轴线（指向喷涂油漆的方向）的旋转无关紧要。因此，喷嘴配置可以用五个坐标来描述：（x，y，z）表示喷嘴的笛卡尔位置，球面坐标（θ，φ）表示喷嘴指向的方向。

任务空间可以写成R3×S2。工作空间可以是R3×S2中的可达点，或者，为了简化可视化，用户可以将工作空间定义为与喷嘴的可达笛卡尔位置相对应的R3子集。

2.6 Summary

机器人是由各种类型的关节连接的连杆机械构造而成的。链接通常被建模为刚体。末端执行器（例如夹具）可以连接到机器人的某个连杆。致动器将力和扭矩传递到关节，从而引起机器人的运动。
最广泛使用的单自由度关节是允许绕关节轴旋转的旋转关节和允许沿关节轴方向平移的棱柱关节。一些常见的两自由度关节包括圆柱关节和万向节，圆柱关节由转动和棱柱关节串联而成，万向节由两个转动关节正交连接而成。球形关节，也称为球窝关节，是一种三自由度关节，其功能类似于人的肩关节。
刚体的配置configuration是对其所有点的位置的规范specification。对于在平面中移动的刚体，需要三个独立的参数来指定配置。对于在三维空间中移动的刚体，需要六个独立的参数来指定配置。
机器人的配置是对其所有环节配置的规范。机器人的配置空间是所有可能的机器人配置的集合。C空间的尺寸是机器人的自由度。
机器人的自由度可以使用Gr ̈ubler's formula $\mathrm{dof}=m(N-1-J)+\sum_{i=1}^{J}f_i,$ ，其中，平面机构的m=3，空间机构的m=6，N是连杆（包括地面连杆）的数量，J是关节的数量，fi是关节i的自由度数量。如果关节施加的约束不是独立的，那么Grüubler公式提供了自由度数量的下界。
机器人的C空间可以显式参数化，也可以隐式表示。对于具有n个自由度的机器人，显式参数化使用n个坐标，这是必要的最小值。隐式表示涉及m≥n的m坐标，其中m坐标服从m−n个约束方程。通过隐式参数化，机器人的C空间可以被视为嵌入更高维度m的空间中的维度n的表面。
结构包含一个或多个闭环的n-dof机器人的C空间可以使用g（θ）=0形式的k个闭环闭合方程隐式表示， $\theta\in{\mathbb{R}^{m}}\mathrm{~and~}g:\mathbb{R}^{m}\rightarrow\mathbb{R}^{k}.$ 这种约束方程称为完整约束。假设θ随时间t变化，则完整约束g（θ（t））=0可以相对于t微分以产生
机器人的运动也可能受到速度约束 $A(\theta)\dot{\theta}=0,$ 其中A（θ）是不能表示为某个函数g（θ）的微分的k×m矩阵。换句话说，不存在任何g（θ），g:Rm→ Rk，使得 $A(\theta)=\frac{\partial g}{\partial\theta}(\theta).$ 这种约束被称为非完整约束或不可积分约束。这些约束降低了系统可行速度的维数，但没有降低可达C空间的维数。在受动量守恒或无滑动滚动约束的机器人系统中出现了非完整约束。
机器人的任务空间是机器人的任务可以自然地表达的空间space。机器人的工作空间是机器人末端执行器可以到达的配置规范specification。