ABSTRACT
虽然FairSC算法能够找到更公平的聚类,但由于计算零空间的内核和显式的密集矩阵的平方根,其代价较高。我们提出了一种新的底层谱计算公式,它结合了零空间投影和霍特林的压缩,这样得到的算法称为s-FairSC,只涉及稀疏的矩阵-向量乘积,并且能够充分利用公平SC模型的稀疏性。在改进的随机块模型上的实验结果表明,s-FairSC与FairSC在恢复公平聚类方面具有可比性。与此同时,对于中等尺寸的模型,它的速度提高了12倍。进一步证明了s-FairSC是可扩展的,因为与没有公平性约束的SC相比,s-FairSC的计算成本只增加了少量。
INTRODUCTION
机器学习(ML)被广泛用于诸如广告目标、信用卡发行和学生录取等领域的自动决策。ML虽然强大,但它很容易受到原始数据中编码的偏差或底层算法对特定群体或个人带来的偏差,从而导致不公平的决策。比如现实生活中算法不公平的例子。在算法决策的背景下,公平通常是指禁止对基于某些群体或个人的自然或后天特征的任何偏袒。这些特征也被称为敏感属性,例如,性别、种族、性取向和年龄组。ML算法日益增长的利益和日益增长的社会影响,推动了学术界和工业界对ML公平性的研究。各种努力已经尝试建模公平和纠正算法偏差在监督和非监督ML。根据算法的选择和公平定义的不同,公平ML有广泛的研究。在本文中,我们主要关注具有群公平性约束的光谱聚类(SC)。群体公平的概念是一种静态平等的概念。它确保了在一个接受积极(消极)考虑的群体中,成员的总体比例与整个人口的比例相同。Kleindessner等人(2019)提出了一个将群体公平概念纳入SC框架的模型,简称FairSC。对于合成网络,FairSC可以以高概率恢复地面真实聚类。此外,FairSC比SC确定了一个更公平的聚类,对真实数据没有公平的限制。不幸的是,由于计算大零空间的标准正交基和稠密矩阵的平方根的计算代价,FairSC只能处理中等程度的问题大小。FairSC不可伸缩。
本文结合零空间投影和霍特林通缩Hotelling deflation,提出了一种新的具有公平约束的SC谱计算公式。新的算法被命名为可扩展的FairSC,或s-FairSC。在s-FairSC中,所有的计算核都只涉及稀疏矩阵-向量乘法,因此能够充分利用公平SC模型的稀疏性。在修正的随机块模型上,s-FairSC与FairSC的比较表明,在中等模型尺寸下,其速度提高了12倍。同时,s-FairSC在恢复公平聚类方面与FairSC具有可比性。s-FairSC被进一步证明是可扩展的,因为与没有公平约束的SC相比,它只有一个计算成本的边际增加。
2 SC AND FAIR SC
2.1 Clustering and fair clustering
给定一组数据,聚类的目标是将该组数据划分为子集,使得同一子集内的数据彼此之间的相似性高于其他子集。数学上,假设 G ( V , W ) G(V, W) G(V,W) 表示具有一组顶点(数据) V = { v 1 , v 2 , . . . , v n } V = \{v_1, v_2, . . . , v_n\} V={v1,v2,...,vn} 和加权邻接矩阵 W = ( w i j ) ∈ R n × n W = (w_{ij} ) ∈ R^{n×n} W=(wij)∈Rn×n 的加权无向图。矩阵 W W W 编码了边的信息。我们假设 w i j ≥ 0 w_{ij} ≥ 0 wij≥0 且 w i i = 0 w_{ii} = 0 wii=0。如果 w i j > 0 wij > 0 wij>0,则 ( v i , v j ) (v_i, v_j) (vi,vj) 是一条边。我们用 d i = ∑ j = 1 n w i j d_i =\sum^n_{j=1} w_{ij} di=∑j=1nwij 表示顶点 v i v_i vi 的度,并用 D = d i a g ( d 1 , d 2 , . . . , d n ) D = diag(d_1, d_2, . . . , d_n) D=diag(d1,d2,...,dn) 表示图 G ( V , W ) G(V, W) G(V,W) 的度矩阵。我们假设没有孤立的顶点,因此 D D D 是正定的。
聚类的任务是将 V 划分为 k 个不相交的子集(簇):

以使得每个子集内部的总权重较大,而不同子集之间的权重较小。聚类(1)可以通过聚类指示矩阵 H = ( h i l ) ∈ R n × k H = (h_{il}) ∈ R^{n×k} H=(hil)∈Rn×k进行编码:
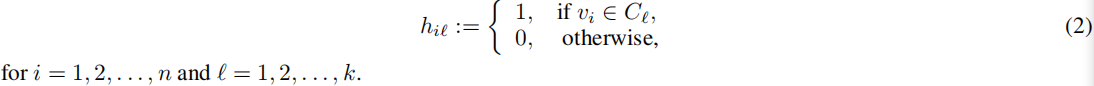
- H H H 是一个 n × k n×k n×k 的矩阵,其中 n 是数据点的数量,k 是聚类的数量。
- 矩阵 H H H 的每一行代表一个数据点,每一列代表一个聚类。
- 如果数据点 i i i 属于聚类 l l l,则 H H H 的第 i i i 行第 l l l 列的元素 h i l h_{il} hil 为 1,否则为 0。
通过调整聚类指示矩阵 H H H,我们可以将数据点分配到不同的聚类中。通过最大化同一聚类内部的权重总和,最小化不同聚类之间的权重总和,我们可以实现将数据点划分为具有相似特征的子集。
现在让我们考虑如何在聚类中实施群体公平性。这里的群体指的是对收集的数据进行划分(例如,基于敏感属性如性别和种族)。我们用 h h h 个非空子集 V 1 , . . . , V h V_1, . . . , V_h V1,...,Vh 来表示这些群体:

其中对于 i ≠ j i \neq j i=j,满足 V i ∩ V j = ∅ V_i ∩ V_j = ∅ Vi∩Vj=∅。聚类的群体公平性是指理想情况下,所有群体中的对象在每个聚类中以比例存在,也称为统计平衡。群体也可以通过群体指示矩阵 G = ( g i s ) ∈ R n × h G = (g_{is}) ∈ R ^{n×h} G=(gis)∈Rn×h 进行编码:
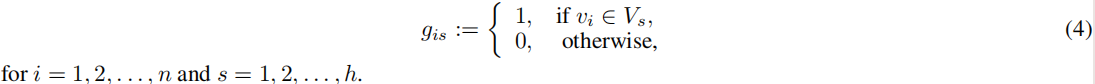
- G G G 是一个 n × h n×h n×h 的矩阵,其中 n n n 是数据点的数量, h h h 是群体的数量。
- 矩阵 G G G 的每一行代表一个数据点,每一列代表一个群体。
- 如果数据点 i i i 属于群体 s s s,则 G G G 的第 i i i 行第 s s s 列的元素 g i s g_{is} gis 为 1,否则为 0。
通过群体指示矩阵 G,我们可以识别数据点所属的群体。在聚类中实施群体公平性意味着努力确保不同群体的对象在聚类结果中按比例存在。
下面的定义是 Kleindessner 等人(2019)扩展了 Chierichetti 等人(2017)关于群体公平性的概念后提出的。
定义 2.1. 对于给定的群体划分 (1),如果在每个聚类中,每个群体的对象按照与原始数据集相同的比例存在,则聚类 (1) 在群体公平性方面是公平的。也就是说,对于 l = 1 , 2 , ⋅ ⋅ ⋅ , k l = 1, 2, · · · , k l=1,2,⋅⋅⋅,k 和 s = 1 , 2 , ⋅ ⋅ ⋅ , h s = 1, 2, · · · , h s=1,2,⋅⋅⋅,h,满足以下条件:
- 对于每个簇 l l l ,群体 s s s 中的对象在簇 l l l 中的比例与群体 s$ 中的对象在原始数据集中的比例相同。
- 即对于每个簇 l l l,满足以下公式:

其中 ∣ V ∣ |V| ∣V∣ 表示集合 V V V 中的顶点数量。
公平性条件(5)可以使用式(2)中的指示矩阵 H H H 和式(4)中的指示矩阵 G G G 来紧凑表示。让我们引入以下符号:
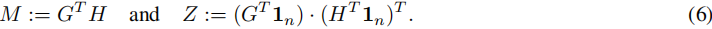
那么,矩阵 M M M 和 Z Z Z 的元素为 m s l = ∣ V s ∩ C l ∣ m_{sl} = |V_s ∩ C_l | msl=∣Vs∩Cl∣ 和 z s l = ∣ V s ∣ ⋅ ∣ C l ∣ z_{sl} = |V_s| · |C_l| zsl=∣Vs∣⋅∣Cl∣,其中 s = 1 , 2 , . . . , h , l = 1 , 2 , . . . , k s = 1, 2, . . . , h,l = 1, 2, . . . , k s=1,2,...,h,l=1,2,...,k。因此,公平性条件(5)等价于以下表达式:

其中 n = ∣ V ∣ n = |V| n=∣V∣。根据公式(6),我们知道公式(7)成立当且仅当:

其中 F 0 : = G − 1 n z T ∈ R n × h , z : = ( G T 1 n ) / n ∈ R h F_0 := G-1_ n z^T ∈ R^{n×h},z := (G^T 1_n)/n ∈ R^h F0:=G−1nzT∈Rn×h,z:=(GT1n)/n∈Rh。观察到向量 z z z 的元素满足 z i = ∣ V i ∣ / n z_i = |V_i|/n zi=∣Vi∣/n,对于 i = 1 , 2 , . . . , h i = 1, 2, . . . , h i=1,2,...,h,根据公式(4)中 G 的定义。
下面的引理表明,在约束条件(8)中,仅使用 F 0 F_0 F0 的前 h − 1 h-1 h−1 列就足够了。使用 F 0 F_0 F0 的前 h − 1 h-1 h−1 列的想法来自 Kleindessner 等人(2019)。在这个想法的基础上,我们通过 F 0 F_0 F0 的秩来证明选择 h − 1 h-1 h−1 的合理性,并证明 h − 1 h-1 h−1 确实是所需的最少列数。
引理 2.1. 设
H
H
H 是由式(2)定义的聚类指示矩阵,
G
G
G 是由式(4)定义的群体指示矩阵。设
F
0
∈
R
n
×
h
F_0 ∈ R^{n×h}
F0∈Rn×h 如式(8)所定义,
F
:
=
F
0
(
:
,
1
:
h
−
1
)
∈
R
n
×
(
h
−
1
)
F := F_0(:, 1 : h − 1) ∈ R^{n×(h−1)}
F:=F0(:,1:h−1)∈Rn×(h−1) 由
F
0
F_0
F0 的前
h
−
1
h-1
h−1 列组成。那么,
(i)
r
a
n
k
(
F
0
)
=
r
a
n
k
(
F
)
=
h
−
1
rank (F_0) = rank (F) = h − 1
rank(F0)=rank(F)=h−1;
(ii) 如果且仅如果聚类 (1) 相对于群体划分 (3) 是群体公平的,那么:

证明:
对于 (i):G 的每一行都只包含一个非零元素等于 1。因此,

因为 G G G 的列是正交的,上面的第一个方程还意味着

其中 G † : = ( G T G ) − 1 G T G^† := (G^T G)^{-1} G^T G†:=(GTG)−1GT 表示 G G G 的伪逆。对于 r a n k ( F 0 ) = h − 1 rank(F_0) = h − 1 rank(F0)=h−1,我们只需证明 F 0 F_0 F0 的零空间的维数为一维。设 x ∈ R p x ∈ R^p x∈Rp 是 F 0 F_0 F0 的零向量,即 F 0 x = 0 F_0x = 0 F0x=0。根据 F 0 F0 F0 的定义,我们有:

将 G † G^† G† 乘以方程,结合方程(38),得到 x = α 1 h x = α1_h x=α1h。另一方面, 1 h 1_h 1h 确实是 F 0 F_0 F0 的零向量:
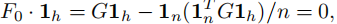
我们使用了(37)。因此, F 0 F_0 F0 的零空间由向量 1 h 1_h 1h 张成。根据秩-零度定理, r a n k ( F 0 ) = h − 1 rank(F_0) = h − 1 rank(F0)=h−1。由 F 0 ⋅ 1 h = 0 F_0 · 1_h = 0 F0⋅1h=0 可知, F 0 F_0 F0 的最后一列是前 h − 1 h − 1 h−1 列的线性组合。因此,我们有 r a n k ( F 0 ) = r a n k ( F ) rank(F_0) = rank(F) rank(F0)=rank(F)。
**对于 (ii):**根据(i),
F
0
F_0
F0 和
F
F
F 具有相同的值域空间。因此,
F
0
T
y
=
0
F_0^T y = 0
F0Ty=0 当且仅当
F
T
y
=
0
F^T y = 0
FTy=0。
然后,根据(8),得出了(ii)。
2.2 SC and fair SC
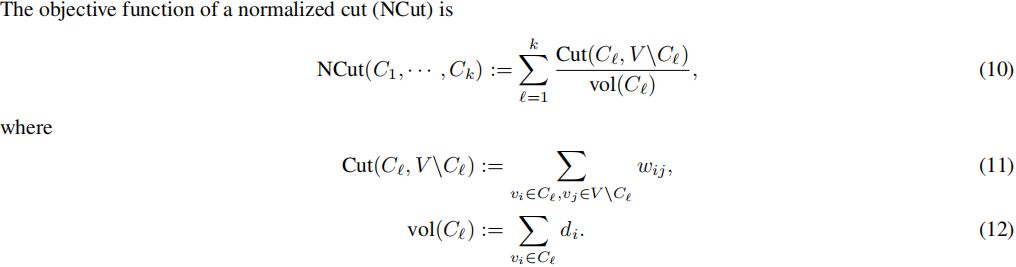
NCut 函数计算跨群簇边缘的缩放总权重。NCut 用于衡量簇之间的相似性:较小的 NCut 表示更好的聚类结果。因此,目标是最小化 NCut。需要注意的是,式(10)中通过 v o l ( C l ) vol(C_l) vol(Cl) 的缩放考虑了簇的大小,以避免异常值的影响。
NCut 函数 式(10)可以使用聚类指示矩阵得到一个简洁的表达式。首先,我们将聚类指示矩阵 H H H 式(2)进行缩放,变为:

其中 D ^ = d i a g ( v o l ( C 1 ) , ⋅ ⋅ ⋅ , v o l ( C k ) ) \hat{D} = diag( \sqrt{ vol(C_1)}, · · · , \sqrt{ vol(C_k)}) D^=diag(vol(C1),⋅⋅⋅,vol(Ck))。我们称新的矩阵 H 为缩放的指示矩阵。为了方便起见,我们对两个指示矩阵使用相同的符号。然后,NCut 函数与矩阵的迹之间存在以下关系:
其中 L = D − W L = D - W L=D−W 是图 G ( V , W ) G(V, W) G(V,W) 的拉普拉斯矩阵。如果 $G(V, W) $是连通的,那么 L L L 是半正定的,并且恰有一个零特征值。
根据(14),NCut 的最小化等价于迹的最小化问题

直接解决问题(15)被证明是 NP 难的。通常会解决以下问题(15)的松弛版本代替:
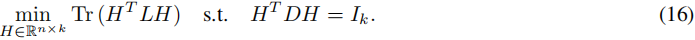 一旦获得了上述的最优解 H,可以通过近似来获得问题(15)的离散解。在这里,通常会应用 k-means 算法(对于 H 的行),但也可以使用其他技术。
一旦获得了上述的最优解 H,可以通过近似来获得问题(15)的离散解。在这里,通常会应用 k-means 算法(对于 H 的行),但也可以使用其他技术。
问题(16)是一个经典的迹最小化问题,最初在 Fan (1949) 中进行了研究。以下定理可以在(Horn 和 Johnson,2012,第248页)中找到。

回到问题(16),我们可以通过变量的改变将其重新表述为标准的迹最小化问题,即 X = D 1 / 2 H X = D^{1/2} H X=D1/2H:
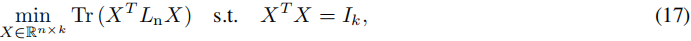
其中 L n = D − 1 / 2 L D − 1 / 2 L_n = D^{-1/2} L D^{-1/2} Ln=D−1/2LD−1/2 被称为归一化拉普拉斯矩阵。根据定理 2.1,问题(17)的最优解 X X X 包含 L n Ln Ln 的 k k k 个最小特征值对应的特征向量。然后,我们可以通过 H = D − 1 / 2 X H = D^{-1/2}X H=D−1/2X 来恢复松弛问题(16)的解,并使用它进行聚类。
我们在算法1中总结了谱聚类(SC)。SC算法由Shi和Malik(2000)以及Ng等人(2001)提出,是一种非常成功的聚类算法。它高效且可扩展,因为它可以利用SC模型的稀疏性,并使用最先进的可扩展稀疏特征求解器。

群体公平性约束可以优雅地融入到谱聚类中。为了实现这一点,可以简单地将线性约束(9)添加到迹最小化问题(16)中,从而得到:
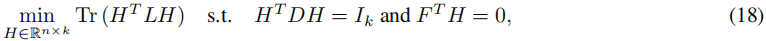
其中 L ∈ R n × n L ∈ R^{n×n} L∈Rn×n 是图拉普拉斯矩阵, F ∈ R n × ( h − 1 ) F ∈ R^{n×(h−1)} F∈Rn×(h−1) 是来自(9)的矩阵,而 F T H = 0 F^T H = 0 FTH=0 是由于 H H H 的缩放(13)而将原始的(9)右乘以 D ^ − 1 \hat{D}^{-1} D^−1 得到的。
在 Kleindessner 等人(2019)的论文中,提出了使用优化问题(18)在谱聚类中实施群体公平性的想法。我们将展示,与仅解决谱聚类相比,(18)中的额外线性约束引入的成本是较小的。
3 FAIR SC ALGORITHMS
在本节中,我们考虑约束迹最小化问题(18)的数值算法。首先回顾 Kleindessner 等人(2019)提出的 FairSC 算法,然后解决 FairSC 算法的可扩展性问题。
3.1 FairSC algorithm
在 Kleindessner 等人(2019)提出的解决问题(18)的基于零空间的算法中,可以按如下方式进行。由于 H H H 的列位于 F T F^T FT 的零空间中,我们可以将 H H H 表示为 H = Z Y H = ZY H=ZY,其中 Y ∈ R ( ( n − h + 1 ) × k ) Y ∈ R^((n−h+1)×k) Y∈R((n−h+1)×k) 且 Z ∈ R ( n × ( n − h + 1 ) ) Z ∈ R^(n×(n−h+1)) Z∈R(n×(n−h+1)) 是 n u l l ( F T ) null(F^T) null(FT) 的正交基矩阵。因此,优化问题(18)等价于以下不带线性约束的迹优化问题:
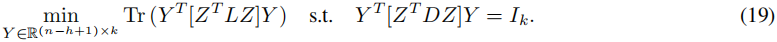
通过变量变换 X = Q Y X = QY X=QY,其中 Q = ( Z T D Z ) 1 / 2 Q = (Z^T DZ)^{1/2} Q=(ZTDZ)1/2,我们可以将(19)转化为标准的迹最小化问题(16)。这导致以下问题:
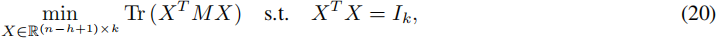
其中 M = Q − 1 Z T L Z Q − 1 M = Q^{-1} Z^T L Z Q^{-1} M=Q−1ZTLZQ−1。观察到 M 是尺寸为 n − h + 1 n - h + 1 n−h+1 的正半定矩阵。根据定理 2.1,问题(20)的解可以通过线性特征值问题 M x = λ x Mx = λx Mx=λx 来求解。最优解 X = [ x 1 , . . . , x k ] X = [x_1, . . . , x_k] X=[x1,...,xk] 包含 M M M 的 k k k 个最小特征值对应的特征向量。最后,将其转换回 H H H,我们有 H = Z Q − 1 X H = ZQ^{-1}X H=ZQ−1X 是问题(18)的解。
我们在算法2中总结了群体公平谱聚类算法FairSC。FairSC算法需要两个主要的计算核心。第一个计算核心是在第2步中计算 F T F^T FT 的零空间。这可以通过对F进行奇异值分解 F = U Σ V T F = UΣV^T F=UΣVT 来实现,其中 U ∈ R n × n U ∈ R^{n×n} U∈Rn×n 和 V ∈ R ( h − 1 ) × ( h − 1 ) V ∈ R^{(h-1)×(h-1)} V∈R(h−1)×(h−1) 是正交矩阵, Σ ∈ R n × ( h − 1 ) Σ ∈ R^{n×(h-1)} Σ∈Rn×(h−1) 是对角矩阵。根据 定理2.1, F F F 的列满秩为 h − 1 h-1 h−1。因此, U ( : , h : n ) U(:, h : n) U(:,h:n) 是 F T F^T FT 的零空间的标准正交基。我们也可以使用 QR 分解 F = U R F = UR F=UR,其中 U ∈ R n × n U ∈ R^{n×n} U∈Rn×n 是正交矩阵, R ∈ R n × ( h − 1 ) R ∈ R^{n×(h-1)} R∈Rn×(h−1) 是上三角矩阵。然后我们可以设置 Z = U ( : , h : n ) Z = U(:, h : n) Z=U(:,h:n)。对于 SVD 和 QR 两种方法,计算复杂度约为 O ( n ( h − 1 ) 2 ) O(n(h-1)^2) O(n(h−1)2)。第二个计算核心是在第3步中计算尺寸为 n − h + 1 n - h + 1 n−h+1 的矩阵的平方根。这可以通过使用块舒尔算法来实现。计算复杂度为 O ( ( n − h + 1 ) 3 ) O((n-h+1)^3) O((n−h+1)3)。对于尺寸较大的矩阵,涉及大型稠密矩阵的这两个计算核心由于内存空间和数据通信成本而计算代价较高。因此,FairSC算法仅适用于中小尺寸的公平谱聚类模型;请参考第4节的数值结果。

3.2 A simple variant of FairSC
作为FairSC的一个简单变体,我们可以首先将优化问题(18)转化为带有线性约束的标准迹最小化问题,然后使用零空间投影来消除约束,而无需计算矩阵的平方根。我们通过变量变换 X = D − 1 / 2 H X = D^{-1/2} H X=D−1/2H,并将优化问题(18)转化为以下形式:

其中 L n = D − 1 / 2 L D − 1 / 2 L_n = D^{-1/2} L D^{-1/2} Ln=D−1/2LD−1/2 是归一化拉普拉斯矩阵, C = D − 1 / 2 F C = D^{-1/2} F C=D−1/2F。请注意,度矩阵 D D D 是对角矩阵,因此生成 L n L_n Ln 和 C C C 只需要进行行和列的缩放。接下来,我们使用零空间基来消除线性约束 C T X = 0 C^T X = 0 CTX=0(在(21)中)。由于 X X X 的列位于 C T C^T CT 的零空间中,我们可以将 X X X 参数化为 X = V Y X = VY X=VY,其中 Y ∈ R ( n − h + 1 ) × k Y ∈ R^{(n-h+1)×k} Y∈R(n−h+1)×k,而 V ∈ R n × ( n − h + 1 ) V ∈ R^{n×(n-h+1)} V∈Rn×(n−h+1) 是 C T C^T CT 零空间的标准正交基矩阵。然后,(21)等价于标准的迹最小化问题:
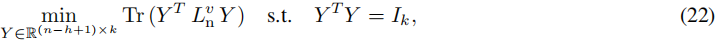
其中 L n v = V T L n V ∈ R ( n − h + 1 ) × ( n − h + 1 ) L^v_n = V^T L_n V ∈ R^{(n-h+1)×(n-h+1)} Lnv=VTLnV∈R(n−h+1)×(n−h+1)。因此,我们可以求解对称特征值问题:

由于特征值问题的解包括与k个最小特征值相对应的特征向量 Y Y Y,我们可以通过这些特征向量来获得方程(22)的解。通过解方程(22),我们可以恢复原始最小化问题(18)的解 H = D − 1 / 2 V Y H = D^{-1/2}VY H=D−1/2VY。
尽管FairSC的这个简单变体避免了计算矩阵平方根,但是 FairSC 的其他缺点仍然存在,即需要显式计算 C T C^T CT 的零空间和计算密集矩阵 L n v L^v_n Lnv 的特征值。
3.3 Scalable FairSC algorithm
现在我们来说明如何重新构造特征值问题(23),以解决 FairSC 剩下的缺点。我们从 L n v L^v_n Lnv 的特征值问题(23)开始:
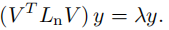
对 V V V 进行左乘得到:

在左侧,由于V的正交性,
V
V
T
⋅
V
y
≡
V
y
V V^T · V y ≡ V y
VVT⋅Vy≡Vy。记
P
=
V
V
T
P = V V^T
P=VVT为一个投影矩阵,投影到V的值域空间(即C^T的零空间)。那么(24)导致了以下投影特征值问题:

其中 x = V y x = Vy x=Vy,而 L n p = P L n P ∈ R n × n L^p_n = P L_n P ∈ R^{n×n} Lnp=PLnP∈Rn×n。因此,特征值问题(23)中的特征值 λ λ λ 也是(23)中的 L n v L^v_n Lnv 的特征值。
投影特征值问题(25)的一个主要优点是它可以通过利用以下事实来避免计算 C T C^T CT 的零空间:

其中 U 2 ∈ R n × ( h − 1 ) U_2 ∈ R^{n×(h-1)} U2∈Rn×(h−1)是空间 C C C 的正交基(回想 [ V , U 2 ] ∈ R n × n [V, U_2] ∈ R^{n×n} [V,U2]∈Rn×n 是正交的)。当 C C C 是一个高瘦矩阵时,这尤其有利,因为 U 2 ∈ R n × ( h − 1 ) U_2 ∈ R^{n×(h-1)} U2∈Rn×(h−1) 比 V ∈ R n × ( n − h + 1 ) V ∈ R^{n×(n-h+1)} V∈Rn×(n−h+1) 要小得多。此外,为了通过迭代特征值求解器计算 L n p L^p_n Lnp 的特征值,我们只需要对于给定的向量 w w w 计算矩阵-向量乘积 L n p w L^p_n w Lnpw,因此 L n p L^p_n Lnp 从未被显式地形成,且可以在不构造 U 2 U_2 U2 的情况下应用 P w P w Pw;请参考第3.3节中的实现细节。
对于FairSC,我们需要 L n v L^v_n Lnv 的 k k k 个最小特征值。为了理解这些特征值与 L n p L^p_n Lnp 的对应关系,我们有以下结果来关联这两个特征值问题(23)和(25)的特征结构。
命题3.1. 假设
L
n
v
L^v_n
Lnv 具有特征分解:

其中
Λ
v
=
d
i
a
g
(
λ
1
,
λ
2
,
.
.
.
,
λ
n
−
h
+
1
)
Λ_v = diag(λ_1, λ_2, ..., λ_{n-h+1)}
Λv=diag(λ1,λ2,...,λn−h+1) 包含特征值,
Y
Y
Y 是一个大小为
n
−
h
+
1
n-h+1
n−h+1 的正交矩阵,包含特征向量。那么从(25)得到的 L_pn具有特征分解:
其中
U
=
[
U
1
,
U
2
]
∈
R
n
×
n
U = [U_1, U_2] ∈ R^{n×n}
U=[U1,U2]∈Rn×n 是正交的,其中
U
1
=
V
Y
∈
R
n
×
(
n
−
h
+
1
)
U_1 = VY ∈ R^{n×(n-h+1)}
U1=VY∈Rn×(n−h+1),
U
2
∈
R
n
×
(
h
−
1
)
U_2 ∈ R^{n×(h-1)}
U2∈Rn×(h−1) 是
C
C
C 值域的任意正交基。
证明:
我们验证(28)是一个特征值分解。首先,由于 V V V 是 C T C^T CT 的零空间的基,而 U 2 U_2 U2 是 C C C 值域的基,我们有 V T U 2 = 0 V^T U_2 = 0 VTU2=0,且
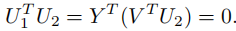
通过快速验证可以得知 U = [ U 1 , U 2 ] U = [U_1, U_2] U=[U1,U2] 满足 U T U = I n U^TU = I_n UTU=In,因此 U U U 是正交的。
另一方面,由
L
n
v
=
V
T
L
n
V
L^v_n = V^TL_nV
Lnv=VTLnV 和
L
n
p
=
P
L
n
P
L^p_n = P L_nP
Lnp=PLnP,我们可以得到:
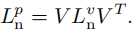
因此,
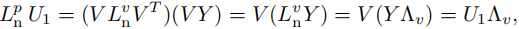
在第三个等式中我们使用了(27)。另一方面, V T U 2 = 0 V^TU_2 = 0 VTU2=0 也意味着:
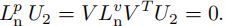
因此, L n p [ U 1 , U 2 ] = [ U 1 , U 2 ] ⋅ b l o c k d i a g ( Λ v , 0 h − 1 , h − 1 ) L^p_n [U_1, U_2]= [U_1, U_2] · blockdiag(Λ_v, 0_{h-1,h-1}) Lnp[U1,U2]=[U1,U2]⋅blockdiag(Λv,0h−1,h−1),即(28)成立。
推论3.1. 设 L n v L^v_n Lnv 和 L n p L^p_n Lnp 如(22)和(25)所定义。那么(i)如果 ( λ , y ) (λ,y) (λ,y) 是 L n v L^v_n Lnv 的特征对,则对应的 ( λ , x ) (λ,x) (λ,x),其中 x = V y x = Vy x=Vy,是 L n p L^p_n Lnp 的特征对。(ii)如果 ( λ , x ) (λ,x) (λ,x)是 L n p L^p_n Lnp 的特征对,并且 C T x = 0 C^Tx = 0 CTx=0,则对应的 ( λ , y ) (λ,y) (λ,y),其中 y = V T x y = V^Tx y=VTx,是 L n v L^v_n Lnv 的特征对。
回到计算 L n v L^v_n Lnv 的 k k k 个最小特征值的过程。由于原始矩阵 L n v L^v_n Lnv 是半正定的,它有 n − h + 1 n-h+1 n−h+1 个特征值,满足, 0 ≤ λ 1 ≤ ⋅ ⋅ ⋅ ≤ λ n − h + 1 0 ≤ λ_1 ≤ · · · ≤ λ_{n-h+1} 0≤λ1≤⋅⋅⋅≤λn−h+1。根据(28),投影矩阵 L n p L^p_n Lnp 具有 n n n个有序特征值: 0 = ⋅ ⋅ ⋅ = 0 ≤ λ 1 ≤ ⋅ ⋅ ⋅ ≤ λ n − h + 1 0 = · · · = 0 ≤ λ_1 ≤ · · · ≤ λ_{n-h+1} 0=⋅⋅⋅=0≤λ1≤⋅⋅⋅≤λn−h+1 ,其中前 h − 1 h-1 h−1 个零特征值(考虑重复)具有 C C C 值域中的特征向量。
在 λ 1 > 0 λ_1 > 0 λ1>0 的简单情况下, L n v L^v_n Lnv 的 k k k 个最小特征值 λ 1 , . . . , λ k λ_1, ..., λ_k λ1,...,λk 对应于 L n v L^v_n Lnv 的 k k k 个最小正特征值。为了找到这些特征值,我们可以首先通过特征值求解器计算 L n p L^p_n Lnp 的 K = k + h − 1 K = k + h - 1 K=k+h−1 个最小特征值,然后选择与非零特征值相对应的 k k k 个特征对(或者选择那些与 C C C 正交的特征值)。然而,如果 λ 1 = 0 λ_1 = 0 λ1=0(或 λ 1 ≈ 0 λ_1 ≈ 0 λ1≈0),那么上述简单的选择方案将无法奏效,因为与 λ 1 = 0 λ_1 = 0 λ1=0 相对应的特征向量与 h − 1 h - 1 h−1 个零特征值的特征空间混合在一起(或者在数值上混合)。特征空间混合问题尤其在使用低精度的迭代方法计算解时会发生。
在接下来的内容中,我们首先讨论Hotelling的缩减方法(Hotelling, 1943),然后展示如何将其应用于解决投影特征值问题(25)的特征值选择问题。Hotelling的缩减方法也被称为显式外部缩减方法,适用于高性能计算。Hotelling的缩减方法的主要思想如下命题所述。
命题3.2. 设一个对称矩阵
M
∈
R
n
×
n
M ∈ R^{n×n}
M∈Rn×n 具有特征值分解:
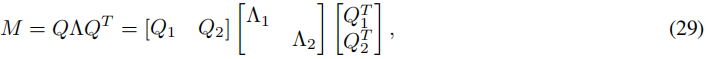
其中 Λ 1 ∈ R k × k Λ_1 ∈ R^{k×k} Λ1∈Rk×k 和 Λ 2 ∈ R ( n − k ) × ( n − k ) Λ_2 ∈ R^{(n−k)×(n−k)} Λ2∈R(n−k)×(n−k) 包含特征值,而 Q 1 ∈ R n × k Q_1 ∈ R^{n×k} Q1∈Rn×k 和 Q 2 ∈ R n × ( n − k ) Q_2 ∈ R^{n×(n−k)} Q2∈Rn×(n−k) 是标准正交特征向量。对于给定的偏移量 σ ∈ R σ ∈ R σ∈R,定义偏移后的矩阵 M σ = M + σ Q 1 Q 1 T M_σ = M + σQ_1Q^T_1 Mσ=M+σQ1Q1T。那么 M σ M_σ Mσ 的特征值分解有如下形式
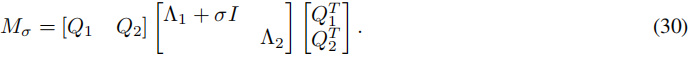
证明:
假设我们对特征值 Λ 2 Λ_2 Λ2 和相应的特征向量 Q 2 Q_2 Q2 感兴趣。根据命题3.2,通过选择足够大的偏移量 σ σ σ, Λ 2 Λ_2 Λ2 中的特征值将始终对应于 M σ M_σ Mσ 的 ( n − k ) (n-k) (n−k) 个最小特征值,因为不需要的特征值 Λ 1 Λ_1 Λ1 被偏移到 Λ 1 + σ I Λ_1 + σI Λ1+σI。所有特征向量保持不变。这正是我们需要将(28)中的 ( p − 1 ) (p-1) (p−1) 个零特征值与其他特征值λi区分开来的方法。
回想一下(28)中 L n p L^p_n Lnp 的特征值分解。为了将不需要的 p − 1 p-1 p−1 个零特征值偏移掉,我们可以应用Hotelling的缩减方法,使用偏移量 σ σ σ 得到:

回想一下 U 2 U_2 U2 是 C C C 的值域的一个标准正交基。如果选择偏移量 σ σ σ,使得 σ > Λ v σ > Λ_v σ>Λv 的第 k k k 小特征值 λ k λ_k λk,则我们所需的 Λ v Λ_v Λv 的 k k k 个最小特征值对应于 L n σ L^σ_n Lnσ 的 k k k 个最小特征值。因此,特征空间混合问题得到解决。
另一方面,根据公式 (26),可以将 (31) 中的偏移矩阵表示为以下形式:
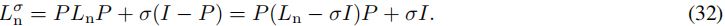
使用
L
n
σ
L^σ_n
Lnσ 进行矩阵-向量乘法仅需要对
P
P
P 和
L
n
L_n
Ln 进行操作。这对于大规模公平性SC模型非常有益。
算法和实现。 正如我们所描述的,通过在投影特征值问题(25)中进行适当选择的 σ σ σ,Hotelling的缩减方法解决了特征值选择问题。总结起来,约束迹最小化问题(18)的解现在可以通过以下命题来刻画。
命题3.3. 设 L n σ ∈ R n × n L^σ_n ∈ R^{n×n} Lnσ∈Rn×n 如式(32)所定义,并假设 σ σ σ 足够大,使得 σ > λ k ( L n v ) σ > λ_k(L^v_n) σ>λk(Lnv),其中 λ k ( L n v ) λ_k(L^v_n) λk(Lnv) 是 L n v L^v_n Lnv 的第 k k k 个最小特征值(参见(23))。那么,如果且仅如果 H = D − 1 / 2 X H = D^{-1/2}X H=D−1/2X,其中 X = [ x 1 , x 2 , . . . , x k ] ∈ R n × k X = [x_1, x_2, ..., x_k] ∈ R^{n×k} X=[x1,x2,...,xk]∈Rn×k 包含与 L n σ L^σ_n Lnσ 的 k k k 个最小特征值对应的 k k k 个特征向量,则 H H H 是迹最小化问题(18)的解。
我们基于投影特征值问题(25)和Hotelling的缩减方法的最终算法在算法3中呈现,简称为可伸缩FairSC算法,简记为s-FairSC。
实现问题 关于s-FairSC,我们讨论了几个实现问题。(i) 对于 L n σ L^σ_n Lnσ 的特征值计算,我们可以使用迭代特征值求解器,比如MATLAB中的eigs函数,它基于ARPACK(Lehoucq等,1998),一种隐式重启Arnoldi方法。特征值求解器只需要通过矩阵向量乘法 L n σ w L^σ_nw Lnσw 来访问 L n σ L^σ_n Lnσ。根据(32),我们有:
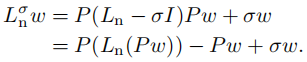

这需要两次使用投影操作与矩阵 P P P。 (ii) 投影P在(26)中可以写作 P = I − C ( C T C ) − 1 C T P = I - C(C^TC)^{-1}C^T P=I−C(CTC)−1CT,参考文献例如Golub等人(2000)。因此, P w Pw Pw 仅需要与矩阵 C C C 进行操作:
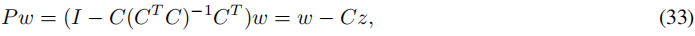
其中 z = ( C T C ) − 1 C T w z = (C^TC)^{-1}C^Tw z=(CTC)−1CTw 是最小二乘问题 m i n z ∥ C z − w ∥ 2 min_z \left \| Cz - w \right \|_2 minz∥Cz−w∥2 的解。对于小到中等规模的问题,可以使用直接的最小二乘求解器求解z。对于大规模问题,可以使用迭代方法如 LSQR (Paige和Saunders, 1982);这与计算 P L n P P L_nP PLnP 的特征值的内外迭代过程是一致的 (Golub等,2000)。 (iii) 对于适当选择的移位 σ σ σ,可以使用 Lin 等人(2021)中推荐的 L n L_n Ln 的最大特征值估计。这样的移位也保证了Hotelling的缩减的数值稳定性 (Lin等,2021)。
3.4 Related work
将优化问题(18)转化为等价的特征值问题的想法非常自然。对于 k = 1 k = 1 k=1 的情况,投影特征值问题(25)在Golub(1973)和(Golub and Van Loan,1996,p. 621)中得到了考虑。
从(25)式得到的投影特征值问题是所谓的约束特征值问题的一种形式,更一般地可以表述为 A x = λ M x Ax = λMx Ax=λMx,满足 C T x = 0 C^Tx = 0 CTx=0 的约束条件,其中 A A A 和 M M M 是对称矩阵, M M M 是正定的。约束特征值问题在许多应用中都会出现。有许多可用的方法;例如,Arbenz 和Drmac(2002)提供了一个针对已知零空间的正半定A的算法;Baker和Lehoucq(2009)提供了一种预处理技术;Golub等人(2000)提供了一种用于处理大型矩阵的内外迭代的Lanczos过程;Porcelli等人(2015)提供了一种在结构有限元代码NOSA-ITACA中的解决过程。
对于许多约束特征值问题,矩阵 C C C 对应于A的零空间,而约束条件 C T x = 0 C^Tx = 0 CTx=0 是为了避免计算“零特征向量”。由于完全避免了A的零空间,因此与我们的问题(25)相比,不存在特征向量选择问题。特别地,Simoncini(2003)提出了一种基于零特征值偏移的约束特征值问题的重新表述。她的方法本质上将Hotelling的缩减作为一种特殊情况,但其目标是将整个A的零空间偏移。通过第3节的讨论,我们展示了Hotelling的缩减也能够将不需要的零向量与所需的向量分开。
4 EXPERIMENTS
4.1 Datasets
Modified Stochastic block model修改的随机块模型(m-SBM)。随机块模型(SBM)(Holland等,1983)是一种具有预定义块(真实聚类)的随机图模型。它被广泛用于生成用于聚类和社区检测的合成网络。为了考虑组公平性,我们利用了Kleindessner等人(2019)提出的修改的SBM(m-SBM)。在m-SBM中,将
n
n
n 个顶点分配给
k
k
k 个簇,以获得预定义的公平真实聚类
V
=
C
1
∪
⋅
⋅
⋅
∪
C
k
V = C_1 ∪ · · · ∪ C_k
V=C1∪⋅⋅⋅∪Ck,并且仅依赖于它们是否属于相同的簇或组的顶点对之间放置边,从而生成图
G
(
V
,
W
)
G(V,W)
G(V,W)(有关详细信息,请参见附录B.1)。假设
V
=
C
1
^
∪
⋅
⋅
⋅
∪
C
k
^
V = \hat{C_1} ∪ · · · ∪ \hat{C_k}
V=C1^∪⋅⋅⋅∪Ck^ 是计算得到的聚类。相对于公平真实聚类的质量通过错误率来衡量:
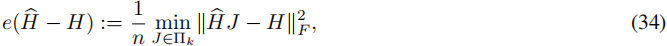
其中,
H
H
H 和
H
^
\hat{H}
H^ 分别是公平真实聚类和计算得到的聚类的指示矩阵,
Π
k
Π_k
Πk 是所有
k
×
k
k×k
k×k 排列矩阵的集合。错误率计算了聚类错误的顶点比例。
FacebookNet是一个小型数据集,对应于2013年法国一所高中学生之间的Facebook友谊关系。该数据集是由Mastrandrea等人(2015)收集的,用于研究人类社交网络、信息传播渠道和观点形成。它也被用于聚类。数据集由两部分组成。一部分包含图 G ( V , W ) G(V, W) G(V,W) 中学生之间的关系。V是学生的集合, n = ∣ V ∣ = 155 n = |V| = 155 n=∣V∣=155, W W W 中的一条边表示两个学生之间的友谊关系。另一部分记录了学生的性别, V = V 1 ∪ V 2 V = V_1 ∪ V_2 V=V1∪V2,其中 V 1 V_1 V1 和 V 2 V_2 V2 分别表示女生和男生, ∣ V 1 ∣ = 70 |V1| = 70 ∣V1∣=70, ∣ V 2 ∣ = 85 |V2| = 85 ∣V2∣=85。
随机拉普拉斯矩阵:为了创建一个随机图 G ( V , W ) G(V, W) G(V,W),我们生成一个维度为 R n × n R^{n×n} Rn×n 的随机对称权重矩阵 W W W,其预设稀疏度为 s = 10 s = 10% s=10,其中 ∣ V ∣ = n |V| = n ∣V∣=n。基于 W W W,计算度矩阵 D D D 和拉普拉斯矩阵 L L L。矩阵 F ∈ R n × ( h − 1 ) F ∈ R^{n×(h-1)} F∈Rn×(h−1) 也被构建为一个随机矩阵。需要注意的是,在这个数据集中,F并不包含组成员信息,只保留了维度信息。该数据集仅用于可扩展性实验。
4.2 Experimental results
**实验4.1:**这个实验是在修改后的SBM上进行的。我们比较了SC、FairSC和s-FairSC的错误率(34式)和运行时间。
图1描述了SC、FairSC和s-FairSC的错误率和运行时间。SC和s-FairSC的测试模型大小从n = 1000增加到10000。由于计算成本较高,FairSC在n = 4000处停止,这与Kleindessner等人(2019)的研究结果相一致。
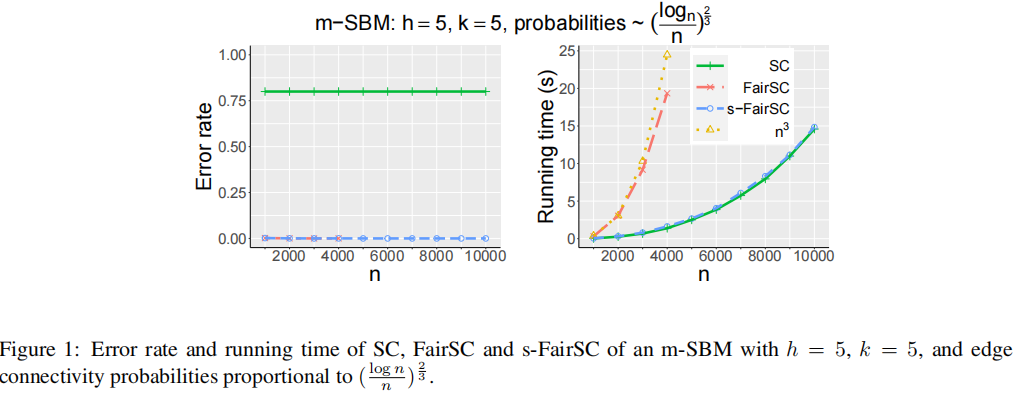
根据图1,我们观察到SC无法恢复公平的真实聚类,而FairSC和s-FairSC都能够恢复公平的真实聚类。就计算得到的聚类的公平性质而言,s-FairSC与FairSC一样公平。然而,s-FairSC的运行时间仅为FairSC的一小部分。例如,当n = 4000时,s-FairSC比FairSC快12倍。我们还观察到,s-FairSC在可扩展性方面与SC(即没有公平性约束)一样可靠。
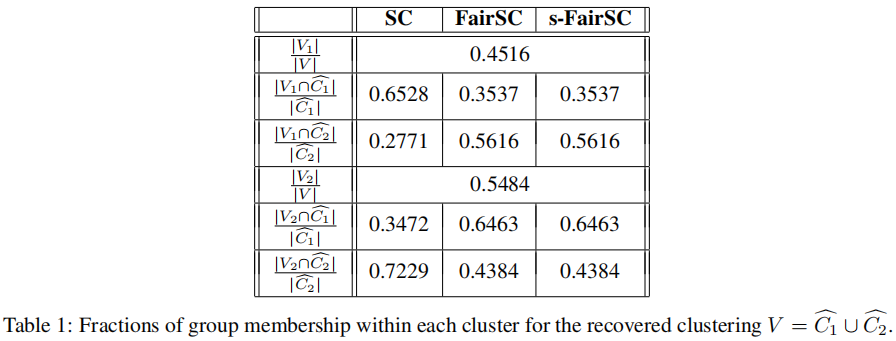
**实验4.2:**在这个实验中,我们使用FacebookNet数据集来量化对精确组公平性的近似程度。表1记录了定义2.1中的数量。
作为替代,可以使用Chierichetti等人(2017)引入的平均平衡概念作为评估聚类的公平性的度量标准。给定一个计算得到的聚类 V = C 1 ^ ∪ ⋅ ⋅ ⋅ ∪ C k ^ V = \hat{C_1} ∪ · · · ∪ \hat{C_k} V=C1^∪⋅⋅⋅∪Ck^ 和组分割 V = V 1 ∪ ⋅ ⋅ ⋅ ∪ V h V = V_1 ∪ · · · ∪ V_h V=V1∪⋅⋅⋅∪Vh,对于 l = 1 , 2 , ⋅ ⋅ ⋅ , k l = 1, 2, · · · , k l=1,2,⋅⋅⋅,k,聚类 C l ^ \hat{C_l} Cl^ 的平衡定义如下:
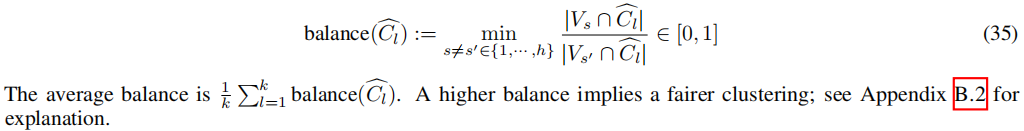

根据表1和图2,我们观察到由于问题(15)被放松为问题(16),因此(5)中的等式不再成立。尽管如此,与SC相比,FairSC和s-FairSC在公平性方面都有所改善。此外,FairSC和s-FairSC产生的结果几乎完全相同。
**实验4.3:**在这个实验中,我们使用随机拉普拉斯矩阵来证明s-FairSC与SC一样可扩展。图3报告了SC和s-FairSC在问题规模从5000到10000时的运行时间。我们观察到,与SC相比,s-FairSC的计算成本只略高一些。
5 CONCLUDING REMARKS
FairSC(Kleindessner等人,2019)能够恢复更公平的聚类,但牺牲了性能和可扩展性。在本文中,我们提出了一种可扩展的FairSC(s-FairSC)。s-FairSC结合了零空间投影和Hotelling的缩减,使得所有的计算核心只涉及稀疏矩阵-向量乘积,并能充分利用公平SC模型的稀疏性。我们使用修改后的SBM来证明s-FairSC在恢复公平聚类方面与FairSC一样准确。与此同时,对于中等规模的SC模型,s-FairSC的速度提高了12倍,并且在计算成本上与没有公平性约束的SC相比,显示出可扩展性的特点,计算成本只有轻微增加。
一个有趣的未来工作问题是开发可扩展的算法,以更宽松的方式解决组公平性条件5。例如,Bera等人(2019)引入了一种具有下界和上界的聚类组公平性概念:
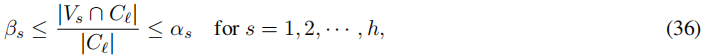
其中βs和αs分别是组Vs的下界和上界,满足0 < βs ≤ αs < 1(见表1中报告的数值数据)。另一个研究课题是将对s-FairSC的研究扩展到个体公平性,即任何两个在特定敏感属性上相似的个体应该被同等对待(Dwork等人,2012;Zemel等人,2013)。Gupta和Dukkipati(2021)提出了一个带有个体公平性约束的SC模型。然而,由于计算核心的高成本,现有算法无法扩展。
























 5592
5592











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








