图片仿射变换矩阵

Nightmare004

已于 2023-03-11 16:26:06 修改

阅读量242

点赞数 1

分类专栏：深度学习数据结构与算法文章标签：矩阵线性代数算法

于 2023-03-11 11:31:12 首次发布

本文链接：https://blog.csdn.net/qq_39942341/article/details/129440487

版权

数据结构与算法同时被 2 个专栏收录

103 篇文章 1 订阅

订阅专栏

深度学习

48 篇文章 2 订阅

订阅专栏

这里用齐次坐标系

平移

$\begin{aligned} x^{\prime} &= x + tx\\ y^{\prime} &= y + ty\\ z^{\prime} &= z + tz\\ \end{aligned}$
于是可以写出
$\begin{pmatrix} x^{\prime}\\ y^{\prime}\\ z^{\prime}\\ 1\\ \end{pmatrix} = \mathbf{T}\left(tx,ty,tz\right) \begin{pmatrix} x\\ y\\ z\\ 1\\ \end{pmatrix}=\begin{pmatrix} 1&0&0&tx\\ 0&1&0&ty\\ 0&0&1&tz\\ 0&0&0&1 \end{pmatrix}\begin{pmatrix} x\\ y\\ z\\ 1\\ \end{pmatrix}$
容易验证,反着平移，也就是求逆
$\left(\mathbf{T}\left(tx,ty,tz\right)\right)^{-1} = \begin{pmatrix} 1&0&0&-tx\\ 0&1&0&-ty\\ 0&0&1&-tz\\ 0&0&0&1 \end{pmatrix} = \mathbf{T}\left(-tx,-ty,-tz\right)$

旋转

2d

绕原点逆时针旋转

$\begin{aligned} x &= r\cos \alpha\\ y & = r\sin \alpha\\ \end{aligned}$
$\begin{aligned} x^{\prime}&= r\cos \beta= r\cos \left(\alpha + \theta\right)\\ y^{\prime}&= r\sin \beta= r\sin\left(\alpha + \theta\right)\\ \end{aligned}$
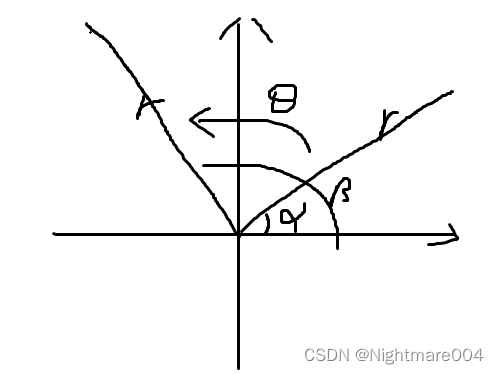
在这里插入图片描述
展开后，容易写出
$\begin{pmatrix} x^{\prime}\\ y^{\prime}\\ \end{pmatrix}=\mathbf{G}\begin{pmatrix} x\\ y\\ \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}\begin{pmatrix} x\\ y\\ \end{pmatrix}$
也就是Givens旋转变换
顺时针旋转，也就是求逆（相当于逆时针旋转 $-\theta$ )
$\mathbf{G}^{-1} = \mathbf{G}^T = \begin{pmatrix} \cos \theta & \sin\theta\\ -\sin\theta & \cos\theta \end{pmatrix}$
齐次坐标里
$\begin{pmatrix} x^{\prime}\\ y^{\prime}\\ 1\\ \end{pmatrix}=\begin{pmatrix} \mathbf{G} &\mathbf{0}\\ \mathbf{0}^T&1\\ \end{pmatrix}\begin{pmatrix} x\\ y\\ 1\\ \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1\\ \end{pmatrix}\begin{pmatrix} x\\ y\\ 1\\ \end{pmatrix}$

绕任意点逆时针旋转

先平移到原点，旋转，再平移回去
假设绕 $\left(c_x,c_y\right)$
$\begin{aligned} \begin{pmatrix} x^{\prime}\\ y^{\prime}\\ 1\\ \end{pmatrix} &= \mathbf{T}\left(c_x,c_y\right)\begin{pmatrix} \mathbf{G} &\mathbf{0}\\ \mathbf{0}^T&1\\ \end{pmatrix}\mathbf{T}\left(-c_x,-c_y\right)\begin{pmatrix} x\\ y\\ 1\\ \end{pmatrix}\\ &= \begin{pmatrix} \cos \theta & -\sin\theta & \left(1-\cos\theta\right)c_x + c_y \sin \theta\\ \sin\theta & \cos\theta & \left(1-\cos\theta\right)c_y - c_x\sin\theta\\ 0 & 0 & 1\\ \end{pmatrix}\begin{pmatrix} x\\ y\\ 1\\ \end{pmatrix} \end{aligned}$
顺时针旋转，也就是求逆（相当于逆时针旋转 $-\theta$ )
$\begin{aligned} \left(\mathbf{T}\left(c_x,c_y\right)\begin{pmatrix} \mathbf{G} &\mathbf{0}\\ \mathbf{0}^T&1\\ \end{pmatrix}\mathbf{T}\left(-c_x,-c_y\right)\right)^{-1} &= \mathbf{T}\left(c_x,c_y\right)\begin{pmatrix} \mathbf{G}^T &\mathbf{0}\\ \mathbf{0}^T&1\\ \end{pmatrix}\mathbf{T}\left(-c_x,-c_y\right)\\ &=\begin{pmatrix} \cos \theta & \sin\theta & \left(1-\cos\theta\right)c_x - c_y \sin \theta\\ -\sin\theta & \cos\theta & \left(1-\cos\theta\right)c_y + c_x\sin\theta\\ 0 & 0 & 1\\ \end{pmatrix} \end{aligned}$

缩放

$\begin{aligned} x^{\prime} &= S_xx\\ y^{\prime} &= S_yy\\ z^{\prime} &= S_zz\\ \end{aligned}$
于是可以写出
$\begin{pmatrix} x^{\prime}\\ y^{\prime}\\ z^{\prime}\\ 1\\ \end{pmatrix} = \mathbf{S}\left(Sx,Sy,Sz\right) \begin{pmatrix} x\\ y\\ z\\ 1\\ \end{pmatrix}=\begin{pmatrix} Sx&0&0&0\\ 0&Sy&0&0\\ 0&0&Sz&0\\ 0&0&0&1 \end{pmatrix}\begin{pmatrix} x\\ y\\ z\\ 1\\ \end{pmatrix}$
求逆
$\left(\mathbf{S}\left(Sx,Sy,Sz\right)\right)^{-1} =\begin{pmatrix} \frac{1}{Sx}&0&0&0\\ 0&\frac{1}{Sy}&0&0\\ 0&0&\frac{1}{Sz}&0\\ 0&0&0&1 \end{pmatrix} =\mathbf{S}\left(\frac{1}{Sx},\frac{1}{Sy},\frac{1}{Sz}\right)$

#!/usr/bin/env python
# _*_ coding:utf-8 _*_
import numpy as np
from cv2 import cv2

path = '000001163.jpg'

if __name__ == '__main__':
    img = cv2.imread(path)
    h, w = img.shape[:2]
    print(img.shape)
    angle = 30
    matrix = cv2.getRotationMatrix2D((w // 2, h // 2), angle, 1)
    rad = np.deg2rad(angle)
    cosine = np.cos(rad)
    sine = np.sin(rad)
    new_h = int(np.round(np.abs(h * cosine) + np.abs(w * sine)))
    new_w = int(np.round(np.abs(w * cosine) + np.abs(h * sine)))
    print(matrix)
    dst = cv2.warpAffine(img, matrix, (new_w, new_h))
    print(dst.shape)
    cv2.imshow("src", img)
    cv2.imshow("dst", dst)
    cv2.waitKey()
    cv2.destroyAllWindows()