CMA-ES 算法初探

最新推荐文章于 2024-04-13 21:43:33 发布

UQI-LIUWJ

最新推荐文章于 2024-04-13 21:43:33 发布

阅读量7.4k

点赞数 11

分类专栏：演化学习文章标签：机器学习算法人工智能矩阵

本文链接：https://blog.csdn.net/qq_40206371/article/details/117091441

版权

演化学习专栏收录该内容

2 篇文章 1 订阅

订阅专栏

1 进化算法

在学习最优模型参数的时候，梯度下降并不是唯一的选择。在我们不知道目标函数的精确解析或者不能直接计算梯度的情况下，进化算法是有效的。

进化算法的灵感来源于自然选择，具有有利于生存的特征的个体可以世代生存，并将好的特性传给下一代；具有不利于生存的特正的个体则会被不断淘汰，最后减少甚至消失。进化是在选择过程中逐渐发生的，进化使得种群可以更好地适应环境。

下面这张图可以很好地解释进化算法的想法，一开始岛上有数量相等的白老鼠和黑老鼠，但是因为黑老鼠和土地的颜色相近，所以老鼠的天敌不易于发现这一种类的老鼠。而白老鼠由于过于显眼，在不断地被吃掉的过程中，慢慢地被淘汰了。久而久之，最后剩的多的就是黑老鼠。

进化算法旨在优化无法直接建模的函数，核心是采样和更新。它在在每一代估计基因型的实值，然后保留最佳的基因型，其他的基因型被丢弃，精英基因被保留并产生。

如下图所示，虚线圆是初始的正态分布，星星表示采样生成的后代，蓝色的星星表示排序后被选中的后代，红色表示没有选中的。那么虚线椭圆就是新一代的概率采样分布。

进化算法作为一种通用的优化方式，可以归纳为：

1，假设我们想优化一个函数f(x)，但f(x)的梯度难以求解。只能得到在特定x下f(x)的确定值。

2，我们认为随机变量x的概率分布p(θ,x)是函数f(x)优化问题的一个较优的解,θ是分布p(θ,x)的参数。我们最终的目标是找到θ的最优配置。

3，在给定分布形式（例如，高斯分布）的情况下，参数 θ 包含了最优解的知识，在一代与一代间进行迭代更新。

4，

2 简单高斯进化策略

即在分布 $N(\mu (t), \sigma ^2(t) I )$ 中随机采样

4，

5，重复（2）-（4）步直到结果足够好

3 协方差自适应进化策略CMA-ES

3.1 基本原理

协方差矩阵自适应演化策略（CMA-ES）通过使用协方差矩阵 C 跟踪分布上得到的样本两两之间的依赖关系，解决了上述这一问题。新的分布参数变为了：

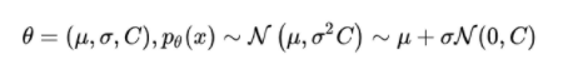
3.1.1 协方差矩阵性质

1，始终都是对角阵

2，始终都是半正定矩阵

3，所有的特征值为非负实数

4，所有的特征向量都是正交的

5，特征向量可以组成一个Rn的标准正交基

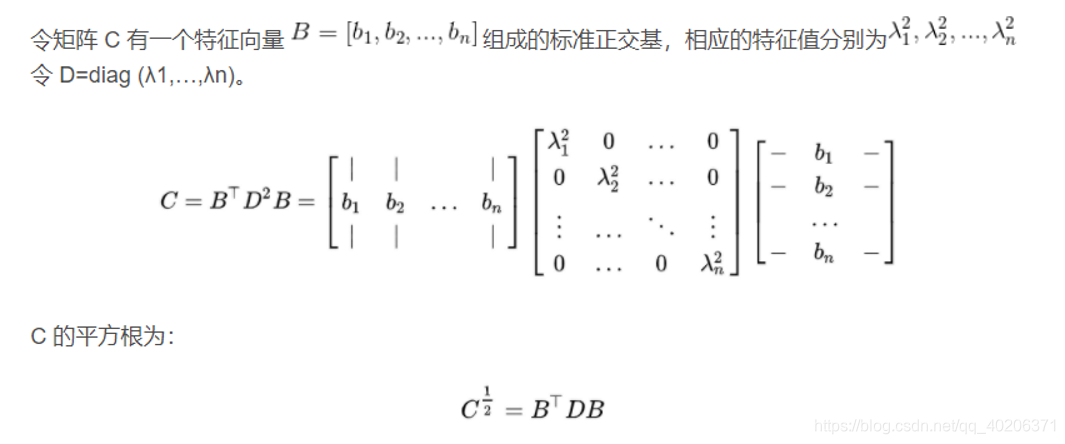
3.1.2 本节涉及符号及其意义

$x_i^{(t)}$ 是在分布 $N(\mu,\sigma ^2 C)$ 上随机采样； $y_i^{(t)}$ 是在分布 $N(0, C)$ 上随机采样。

$\mu ^{(t)}$ 是第t代的平均值； $\sigma ^{(t)}$ 是第t代采样时候的步长; $C ^{(t)}$ 是第t代的协方差矩阵。

$B ^{(t)}$ 和 $D ^{(t)}$ 是 $C ^{(t)}$ 进行特征值分解的结果（见3.1.1）。

$p_\sigma ^{(t)} , p_c ^{(t)}$ 是第t代步长σ和协方差矩阵C的进化路径

$\alpha_\mu, \alpha_\sigma, \alpha_{cp}, \alpha_{c \lambda}, \alpha_{c 1}$ 分别是μ,σ,pc,C的两种路径（后文会涉及）的学习率

$d_\sigma$ 是步长σ更新时候的阻尼系数

3.1.3 更新均值

μ的学习率为1的时候，就是

3.1.4 控制步长

即 $C^{(t) \frac{1}{2}} \sum y_i$ ~N(0,I) （第二行式子是因为每一个yi都是N(0,C)中采样的）

有了演化路径之后，我们就可以根据演化路径来更新我们的σ进化路径了

注：这里公式有一处笔误，第二行根号里面第一项为 $\alpha_\sigma$

注：这里调整步长的思想来源于CSA-ES（累积步长调整策略），这种思路使用多代来记录同一条路径，即进化路径。演化路径是连续几代路径的总和，在每次迭代中对多个精英子代的搜索方向做加权平均，相反分量相互抵消，相同分量进行叠加。如果成功的步骤都朝着相同的方向发展累加起来，那么该方向的发展路径就会相对较长，我们可以用一个较大的步长来代替该方向的总进化距离；反之，则需要简短步长，即：

3.1.4.1 Polyak算法回忆

3.1.5 调整协方差矩阵

看起来是可以的，但是只有当我们选择出的种群足够大，上述估计才可靠。然而，在每一代中，我们希望使用较小的样本种群进行快速的迭代。这就是 CMA-ES 发明了一种更加可靠，但同时也更加复杂的方式去更新 C 的原因。它包含两种独立的演化路径：

注：n是每个样本的维度，λ是每一代取的精英样本数

3.2 总体CMA-ES

这是一篇论文里面的CMA-ES的总体方案；第一步取值；第二步挑精英值；第三步，更新均值μ；第四步更新步长σ需要的演化路径 $p_\sigma ^{(t)}$ ；第五步更新步长；第六步更新path2 需要的C的演化路径；第七步我个人觉得不需要？（同时在另一篇论文“基于改进的CMA_ES的仿真足球机器人的行走优化”里面，也是直接第八步的，这个欢迎讨论哈！）；第八步更新协方差矩阵

UQI-LIUWJ

关注

11
点赞
踩
50

收藏

觉得还不错? 一键收藏
打赏
0
评论
CMA-ES 算法初探

1 进化算法在学习最优模型参数的时候，梯度下降并不是唯一的选择。在我们不知道目标函数的精确解析或者不能直接计算梯度的情况下，进化算法是有效的。进化算法的灵感来源于自然选择，具有有利于生存的特征的个体可以世代生存，并将好的特性传给下一代；具有不利于生存的特正的个体则会被不断淘汰，最后减少甚至消失。进化是在选择过程中逐渐发生的，进化使得种群可以更好地适应环境。下面这张图可以很好地解释进化算法的想法，一开始岛上有数量相等的白老鼠和黑老鼠，但是因为黑老鼠和土地的颜色相近，所以老鼠的天敌不易于发现这一种类
复制链接

扫一扫