机器学习笔记：卡尔曼滤波

UQI-LIUWJ

已于 2023-02-08 22:25:39 修改

阅读量4.8k

点赞数 2

分类专栏：机器学习文章标签：人工智能

于 2022-07-12 19:02:52 首次发布

本文链接：https://blog.csdn.net/qq_40206371/article/details/125741593

版权

机器学习专栏收录该内容

157 篇文章

订阅专栏

1 滤波

滤波的作用就是给不同的信号分量不同的权重
- 比如低通滤波，就是直接给低频信号权重1；高频信号权重0
- 降噪可以看成一种滤波：降噪就是给信号一个高的权重而给噪声一个低的权重

1.1 滤波、插值与预测

插值（interpolation）

平滑（smoothing）

用过去的数据来拟合过去的数据

滤波（filtering）

用当前和过去的数据来求取当前的数据

预测（prediction）

用当前和过去的数据来求取未来的数据

2 卡尔曼滤波

卡尔曼滤波器由一系列递归数学公式描述。它们提供了一种高效可计算的方法来估计过程的状态，并使估计均方误差最小。
卡尔曼滤波器应用广泛且功能强大：它可以估计信号的过去和当前状态，甚至能估计将来的状态，即使并不知道模型的确切性
Kalman Filter 只能减小均值为0的测量噪声带来的影响。只要噪声期望为0，那么不管方差多大，只要迭代次数足够多，那效果都很好。反之，噪声期望不为0，那么估计值就还是与实际值有偏差。

2.1 图示卡尔曼滤波的作用

我们考虑一辆小车在一条直线上行驶。
如果我们知道小车的运动方向、所受的力、质量等等参数，以及小车的初始状态，理论上我们可以求出它任意时刻的状态
但是小车内部（小车结构、车轮质地等）以及小车外部（环境因素）等可能存在不确定因素（噪声），这会导致小车不一定正正好好在预测的位置，会存在一定的噪声
——>我们假设每种不确定因素（噪声）都满足正态分布，那么我们可以据此对小车的位置进行估计：

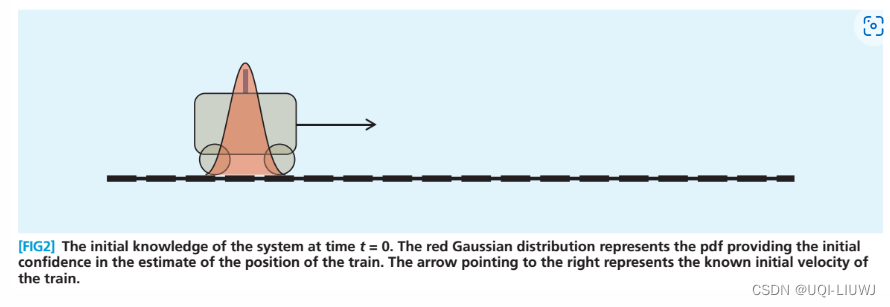
根据小车的运动方程、小车的属性，我们可以估计处小车在下一时刻的位置

小车运动过程中，会不断地收到噪声的影响，因而t=1时刻方差（不确定性）比t=0时刻还要大。

为了避免纯理论估计估计带来的偏差，在 t=1 时刻对小车的位置坐标进行一次测量，当然对小车距离的测量也会受到种种不确定因素的影响，所以小车t=1 时的测量位置服从蓝色的正态分布：

于是我们得到了两个不同的分布，都是来描述小车的位置的。那么应该怎么结合这两个分布呢？

卡尔曼滤波的作用是找一个权重，将二者加权平均，合并为绿色的正态分布。那个就是卡尔曼滤波的结果

2.2 离散卡尔曼滤波

2.2.1 过程状态

注：这一小节的上下标和之后卡尔曼滤波的部分会有一定的差异

离散卡尔曼滤波器用于估计离散时间过程的状态变量 $x \in R^n$ （小车的方向，速度等）

这个离散时间过程由以下离散随机差分方程描述：

$X_k=F_k \cdot X_{k-1}+B_k \cdot U_k +W_k$

$X_k$	估计的当前状态
$X_{k-1}$	上一时刻的状态
$U_k$	输入值
$W_k$	噪声（满足正态分布） $p(w) \sim N(0,Q)$

定义观测变量 $z \in R^m$ （小车的位置），我们有： $Z_k=H_k \cdot X_k +V_k$

$Z_k$	当前时刻的观测变量
$X_k$	当前状态变量
$V_k$	噪声（和W独立，且也满足正态分布） $p(V) \sim N(0,R)$

2.2.2 时间更新方程

时间更新方程根据上一时刻（k－1 时刻) 的后验估计值，推算当前状态变量和误差协方差估计的值
- 先验估计
- 用来得到小车例子中的红色部分

更新方程如下：

$\hat{x_k}^-=F \cdot \hat{x_{k-1}}+B\cdot u_k$

$P_k^-=F\cdot P_{k-1}\cdot F^T+Q$

$\hat{x_k}^-\in R^n$

( − 代表先验，

^ 代表估计)
已知第 k 步以前状态情况下，第 k 步的先验状态估计
$\hat{x_{k-1}}$
知道测量变量 $Z_{k-1}$ 之后，第k-1步的后验状态估计

（第k-1步卡尔曼滤波的结果）

F（后面的A）
将上一时刻k−1 的状态变量线性映射到当前时刻 k 的状态转换矩阵
实际中 F应随时间变化，这里假设为常数。
B 控制输入矩阵，假设为常数
$U_k$ 输入值
$P_k^-$ 先验协方差

——>通过时间更新方程，我们得到k时刻状态变量的先验估计（均值） $\hat{x_k}^-$ 和先验协方差估计 $P_k^-$

2.2.2.1 先验协方差估计 $P_k^-$ 的推导

记先验和后验估计的误差为

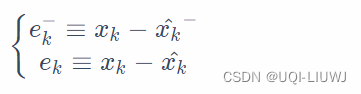
于是先验和后验估计的协方差矩阵为

我们接下来推导 $P_k^-$

2.2.3 测量（状态）更新方程

使用当前时刻的测量值来更正预测阶段估计值，得到当前时刻的后验估计值。

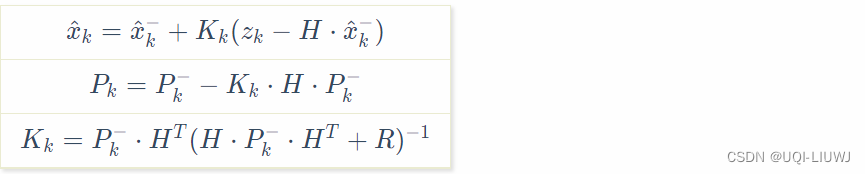
测量状态方程的顺序是：

计算卡尔曼增益 Kk （第三行）
- 作用是使后验估计误差协方差 Pk 最小
- - 观测误差的协方差矩阵R越大（观测的准确性越不能得到保障），越小（变相地先验预测的权重越大）
    - 如果观测误差的协方差矩阵R趋近于0——> $K_k$ 趋近于1/H
  - 先验协方差估计越小（观测的准确性有保障），越小（先验预测的权重越大）
    - 如果先验协方差估计 $P_k^-$ 趋近于0——> $K_k$ 趋近于0
测量输出以获得 Zk
产生k时刻状态的后验估计（第一行）
- 先验估计 $\hat{x_k}^-$ 、测量变量Zk和预测 $H \cdot \hat{x_k}^-$ 的差【测量过程的观测值和预估值之间的差异】，这两项的线性组合
估计状态的后验协方差Pk （第二行）

——>

2.3 卡尔曼滤波的迭代

上一时刻计算得到的后验估计被作为下一时刻计算的先验估计

3 python实现

3.0 参数设置

令：

真实值x	-0.377
A（观测状态——>状态变量）	1
H（状态变量——>测量值）	1
R（测量噪声协方差）	0.01
Q（过程激励噪声协方差（系统过程的协方差））	1e-5

3.1 手动实现

3.1.1 导入库

import numpy  
import pylab
#导入库

n_iter = 50  
sz = (n_iter,)  
x = -0.37727 # 真实值  
z = numpy.random.normal(x,0.1,size=sz) 
# 50个观测值 ,观测时存在噪声
#n_iter个样本点

3.1.2 参数设置

xhat=numpy.zeros(sz)      
# x 滤波估计值 （后验）

P=numpy.zeros(sz)         
# 滤波估计协方差矩阵  (后验)

xhatminus=numpy.zeros(sz) 
#  x 估计值  （先验）

Pminus=numpy.zeros(sz)    
# 估计协方差矩阵  （先验）

K=numpy.zeros(sz)         
# 卡尔曼增益

Q = 1e-5 
# 过程激励噪声协方差

xhat[0] = 0.0  
P[0] = 1.0 
R=0.01

3.1.3 卡尔曼滤波

for k in range(1,n_iter):  
    # 预测  
    xhatminus[k] = xhat[k-1]  
    #^X_k_=A^X_{k-1}+BU(k-1) 
    #A=1, 这里没有输入，所以U= 0  

    Pminus[k] = P[k-1]+Q     
    #Pk_=AP_{k-1}A^T+Q
     


    # 更新  
    K[k] = Pminus[k]/( Pminus[k]+R ) 
    #K(k)=Pk_H'/[HPk_H' + R]
    #H=1  

    xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) 
    #X_k = X_k_ + K(k)[Z(k) - HX_k_], H=1  

    P[k] = (1-K[k])*Pminus[k] 
    #Pk = (1 - K(k)H)Pk_, H=1

3.1.4 绘制结果

pylab.figure()  
pylab.plot(z,'k+',label='noisy measurements')     
#观测值  
pylab.plot(xhat,'b-',label='a posteri estimate')  
#滤波估计值  
pylab.axhline(x,color='g',label='truth value')    
#真实值  
pylab.legend()  
pylab.xlabel('Iteration')  
pylab.ylabel('Voltage')

3.2 使用filterpy包

3.2.1 导入库

from filterpy.kalman import KalmanFilter
import numpy as np


n_iter = 50  
sz = (n_iter,)  
x = -0.37727 # 真实值  
z = numpy.random.normal(x,0.1,size=sz) 
# 50个观测值 ,观测时存在噪声
#n_iter个样本点

3.2.2 参数设置

kf = KalmanFilter(dim_x=1, dim_z=1)
kf.F = np.array([1])
kf.H = np.array([1])
kf.R = np.array([0.1**2])
kf.P = np.array([1.0])
kf.Q = 1e-5 
xhat[0] = 0.0  
P[0] = 1.0

3.2.3 训练

for k in range(1,n_iter):  
    kf.predict()
    xhat[k] = kf.x
    kf.update(z[k], 0.1**2, np.array([1]))

3.2.4 画图

pylab.figure()  
pylab.plot(z,'k+',label='noisy measurements')     
#观测值  
pylab.plot(xhat,'b-',label='a posteri estimate')  
#滤波估计值  
pylab.axhline(x,color='g',label='truth value')    
#真实值  
pylab.legend()  
pylab.xlabel('Iteration')  
pylab.ylabel('Voltage')