矩阵的条件数、奇异值分解（SVD)

最新推荐文章于 2025-06-29 12:13:28 发布
原创 最新推荐文章于 2025-06-29 12:13:28 发布 · 2.4k 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

矩阵条件数是衡量矩阵运算稳定性的关键指标，它描述了矩阵对输入向量的放大或压缩效应。大条件数意味着矩阵操作可能导致数值误差显著增加。奇异值分解（SVD）则提供了一种对任意矩阵进行分解的方法，即使在非方阵情况下。SVD将矩阵分解为酉矩阵U、奇异值矩阵Σ和酉矩阵V，奇异值决定了矩阵的秩和条件数。在数值计算中，SVD常用于求解病态问题，因为其能揭示矩阵的弱和强特征。

矩阵的条件数（condition number）是数值分析和线性代数中的一个重要概念，它刻画了矩阵某方面的特性。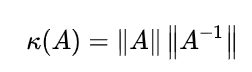在这里插入图片描述
为矩阵 A 的条件数。结合上面提到的几何意义，条件数同时描述了矩阵A 对向量的拉伸能力和压缩能力，换句话说，令向量发生形变的能力。条件数越大，向量在变换后越可能变化得越多。

奇异值分解（SVD）也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：
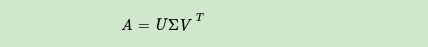
在这里插入图片描述
其中 U是一个 m * m 的矩阵， Σ \Sigma Σ 是一个m * n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个n * n的矩阵。
U 和 V都是酉矩阵，即满足
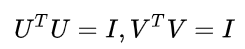
在这里插入图片描述

矩阵奇异值分解算法（SVD）详解
最新发布
qq_36812406的博客
09-18 1799
给定任意实矩阵A∈Rm×n，它的**奇异值分解（SVD）**是AUΣV⊤其中U∈Rm×m是正交矩阵（列为m个正交单位向量），U⊤UIm​；V∈Rn×n是正交矩阵，V⊤VIn​；Σ∈Rm×n是对角（严格说是对角块）矩阵，形如Σdiagσ1​σr​0​00​其中σ1​≥σ2​≥⋯≥σr​0为rrankA。通常写成AUr​Σr​Vr⊤​。
奇异值分解（《矩阵分析》阅读笔记）
m0_52951250的博客
04-23 2181
m×n m×m m×n n×n 1.若A的秩等于r，U的前r列组成A的列空间的标准正交基 U的后n-r列组成A的左零空间的标准正交基 V的前r列组成A的行空间的标准正交基 V的后m-r列组成A的零空间的标准正交基 2.定理：若一矩阵有零奇异值，那么该矩阵一定是奇异的（秩亏缺的） ...
矩阵的条件数、范数、奇异值、特征值
weixin_36347462的博客
05-31 7192
矩阵的条件数 矩阵的条件数用来衡量一个矩阵是“良态的”还是“病态的”。 条件数越大，矩阵越接近于奇异矩阵（不可逆矩阵），矩阵越“病态”。在数值计算中，矩阵的条件数越大，计算的误差越大，精度越低。 如Ax=b中，对A中元素加上一个小扰动，解x的变化都会非常大。 范数 Frobenius范数： 诱导范数 向量Lp范数： 1范数： 2范数： 无穷范数： 奇异值 其中奇异值是按从大到小的顺序排列的 特征值 A是n阶方阵，如果存在常数λ和n维非零列向量x，使得等式Ax=λx成立，称λ为A的特征值，x
数值分析：矩阵求逆-奇异性、条件数
热门推荐
皮皮blog
08-18 3万+
http://blog.csdn.net/pipisorry/article/details/52241141本blog主要内容有：矩阵的奇异性、条件数与病态矩阵、矩阵求逆。奇异矩阵和非奇异矩阵singular matrix&nonsingular matrix概念和定义若n阶矩阵A的行列式不为零，即 |A|≠0，则称A为非奇异矩阵或满秩矩阵，否则称A为奇异矩阵或降秩矩阵。奇异矩阵是线性代数的概念
条件数、奇异值与海森矩阵
Zachzqh的博客
08-09 5178
问题 CS231n: Convolutional Neural Networks for Visual Recognition  / Lecture7: Training Neural Networks, Part 2 在讲到 Optimization: Problems with SGD 时，有这样一段话： As we go up and down in this land...
矩阵的条件数（condition number）
zxs1010的博客
05-14 8797
从优化或者数值计算的角度来说，L2 范数有助于处理 condition number 不好的情况下矩阵求逆很困难的问题。 κ(A)=∥A∥∥A-1∥ 如果方阵 A 是奇异的，那么 A 的 condition number 就是正无穷大了。实际上，每一个可逆方阵都存在一个 condition number。 对condition number来个一句话总结：condition numbe...
机器学习算法：奇异值分解SVD
天涯雨的博客
06-29 1063
机器学习算法：奇异值分解SVD
奇异值分解SVD及其应用
AI天才研究院
05-28 1138
奇异值分解SVD及其应用 1.背景介绍 1.1 什么是奇异值分解(SVD) 奇异值分解(Singular Value Decomposition, SVD)是一种线性代数分解技术,可将任意矩阵分解为三个矩阵的乘积形式。SVD在许多领域都有广泛
SVD奇异值分解——矩阵压缩
WL的博客
07-20 871
图片矩阵压缩SVD
矩阵的奇异值分解
10-25
### 矩阵的奇异值分解（SVD） 在探讨机器人的性能指标时，雅克比矩阵成为了一个关键的研究对象。然而，雅克比矩阵往往不是方阵，这为直接应用传统的线性代数方法带来了挑战。为了克服这一难题，奇异值分解（SVD）...
矩阵的“特征值分解”和“奇异值分解”区别
Wenfei Wang的专栏
01-08 1262
转载（http://blog.163.com/to_be_myself/blog/static/176060227201101253441822/）        特征值分解处理相关矩阵，奇异值分解处理数据矩阵，两者结果相同，特征值分解可以采用K-L变换，奇异值分解可以借助于svd 。svd可以用于求矩阵的伪逆，也可以用来实现降维，K-L变换可以用在信号编码和数据压缩领域 关
矩阵条件数的定义、理解以及matlab代码
hm__2016的博客
11-07 3550
cond⁡(A)=∥A∥∙∥A−1∥cond(A)=∥A∥∙∥∥​A−1∥∥​,其中∥⋅∥\|\cdot\|∥⋅∥代表的是矩阵范数,那么什么是矩阵范数呢矩阵范数需要满足以下三点要求a.正定性 ||A||≥0，only when A为0矩阵，||A|| = 0b.齐次性c.三角不等式如果除了满足上面三点要求外，还满足第四点要求，则称为服从乘法范数（sub-multiplicative norm）d.相容性。
24矩阵——条件数与方程组的性态、“病态”矩阵与方程、系数矩阵与右端微小扰动情况、条件数的几何意义
炫云云
05-30 1432
💖💖感谢各位观看这篇文章，💖💖点赞💖💖、收藏💖💖、你的支持是我前进的动力！💖💖 💖💖感谢你的阅读💖，专栏文章💖持续更新！💖关注不迷路！!💖 矩阵线性代数笔记整理汇总，超全面_ 文章目录 “病态”矩阵与方程 条件数 系数矩阵与右端微小扰动情况 条件数的几何意义 参考
浅谈条件数（condition number）
weixin_45925418的博客
06-20 3531
浅谈条件数（condition number） 目录浅谈条件数（condition number）向量的范数（the norm of a vector）矩阵的范数（the norm of a matrix）三条结论结论1结论2结论3总结参考资料 近日在看线代的书时，正好看到了奇异值（singular value）在计算条件数的应用，于是找了几份资料，似有所悟，在此现学现卖，分享与同道中人。 需要指出的是，条件数是个宽泛的概念，这里讨论的，用[1]的话说是“the condition number for i
分块矩阵求解：条件数与稳定性
AI天才研究院
01-07 1467
1.背景介绍 分块矩阵求解是一种常见的线性代数计算方法，主要用于解决大规模矩阵计算问题。在现代计算机科学和工程技术中，分块矩阵求解技术已经成为了一种重要的计算方法，它可以有效地解决大规模的线性方程组问题。然而，分块矩阵求解也存在一些挑战，其中最主要的问题是条件数和稳定性问题。在本文中，我们将讨论分块矩阵求解的条件数与稳定性，以及如何解决这些问题。 2.核心概念与联系 在分块矩阵求解中，我们需...
SVD奇异值分解（Singular Value Decomposition）
曹浩洋的专栏
07-17 1140
奇异值分解（Singular Value Decomposition）是线性代数中一种重要的矩阵分解，是矩阵分析中正规矩阵酉对角化的推广。在信号处理、统计学等领域有重要应用。 假设M是一个m×n阶矩阵，其中的元素全部属于域 K，也就是 实数域或复数域。如此则存在一个分解使得 其中U是m×m阶酉矩阵；Σ是半正定m×n阶对角矩阵；而V*，即V的共轭转置，是n×n阶酉矩阵
SVD和PCA
思君苑
11-02 3002
说明：此处的LDA对应于Linear Discriminant Analysis，PLDA即对应于Probabilistic LDA. 该代码对应的文章为ICCV2007 paper Probabilistic Linear Discriminant Analysis for Inferences About Identity，源代码可以从 Prince Vision Lab处下载。虽然源
（四）矩阵的条件数
AlbertM的博客
10-02 1446
本文主要内容如下： 1. 矩阵的条件数 2. 条件数的性质 3. 误差与残差
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值