在此记录一些需要理解的概念
超平面的表达
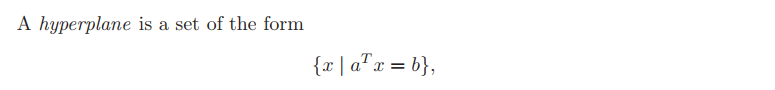
超平面可以看成是
a
T
(
x
−
x
0
)
=
0
a
T
x
=
a
T
x
0
=
b
[
将
a
T
x
0
记
为
b
]
a^T(x-x_0)=0\\a^Tx=a^Tx_0 =b \ \ \ \ [将a^Tx_0记为b]
aT(x−x0)=0aTx=aTx0=b [将aTx0记为b]
相应的，超平面也就分出了两个半空间
a
T
x
≥
b
=
a
T
x
0
a
T
(
x
−
x
0
)
≥
0
a^Tx\ge b=a^Tx_0\\ a^T(x-x_0)\ge0
aTx≥b=aTx0aT(x−x0)≥0
我们知道当两个向量夹角小于九十度的时候内积大于等于0，所以大于等于的半空间就是在法向量a一侧的半空间
向量不等式
对于多个不等式的合成写法，向量不等式（所以这类序并不像定义在R上的序，要么是大于要么是小于，可能整个向量不等式里一部分大于一部分小于，不一定能比较）
半正定锥，正定锥
广义不等式
回顾锥的定义
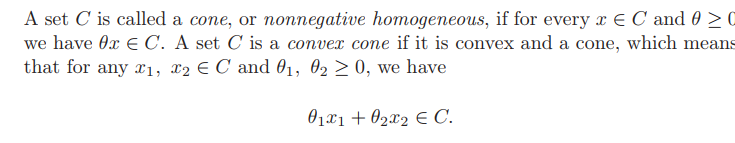
凸和闭都好理解，实的是什么意思？
- 非空内部 ，因为锥可以是一条射线，内部为空
- 尖的，因为锥可以是一个双向的锥（领结型），两个关于某点对称的锥，这就排除了这一种情况
广义不等式是
R
n
R^n
Rn上的半序关系，用proper cone
K
∈
R
n
K\in R^n
K∈Rn来定义
对偶锥和广义不等式
对偶锥一定是凸的，也就是说可以看作是原锥的一个凸近似。
在广义不等式下定义极小元minimal和最小元minimum，需要注意最小元是所有元素都可比较（半序关系不一定非黑即白），他是最小的，极小元是在可以比较的点里比它小的和S的交集只有他一个。
目前对对偶锥和对偶广义不等式的理解是这样的。
- 广义不等式是定义在正常锥下的一种关系
- 用对偶锥定义的对偶广义不等式和原广义不等式之间可以相互转换
- 可以用对偶广义不等式描述原广义不等式下的关系
- 原广义不等式下的关系可能不太好判断？用对偶广义不等式表达可能更好判断？
2192
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
