【物理学】电磁学——麦克斯韦方程组

【物理学】电磁学——麦克斯韦方程组

---

前言

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、麦克斯韦之前的电磁学

对3式，即法拉第定律计算散度，等式左右为0，没问题

对4式，即安培定理计算散度，等式左边为0，右边出现问题，不一定为0；
对于稳恒电流，J散度为0，但若电流不稳定，J散度不一定为0

二、麦克斯韦如何修改安培定理

使用连续性方程及高斯定理，即1式，可推出

修改4式，可得安培-麦克斯韦定理

其积分形式

具体解释

三、麦克斯韦方程组

1.高斯电场定律

麦克斯韦方程处理的两类电场，一类是电荷产生的静电场，一类是变化磁场产生的感生电场
高斯电场定律处理的是静电场

1.积分形式——处理电场在整个曲面

电荷产生电场，电场通过任意闭合曲面的通量正比于曲面所包含的电荷总量

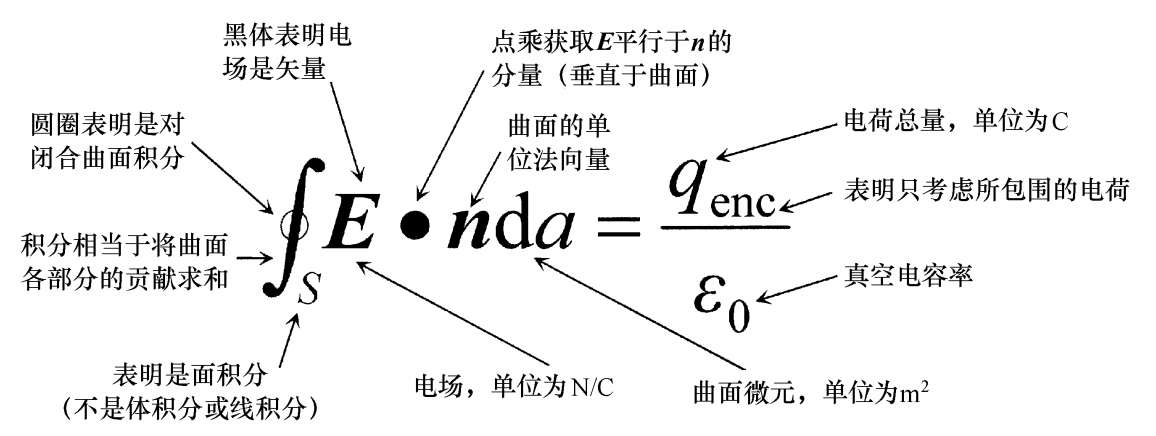
2.微分形式——处理空间中一点处的电场

电荷产生的电场从正电荷散开，汇聚到负电荷

2.高斯磁场定律

1.积分形式

穿过任意闭合曲面的总磁通量为0

2.微分形式

磁场的散度处处为0

3.法拉第定律

1.积分形式

穿过一个曲面的磁通量的变化会在该曲面的任意边界路径上感生出电动势，为感应电动势，并且变化的磁场会感生出环绕的磁场

2.微分形式

随着时间变化的磁场会产生出环绕的电场

4.安培-麦克斯韦定律

1.积分形式

穿过曲面的电流或变化的电通量会产生沿曲面边界的环绕磁场

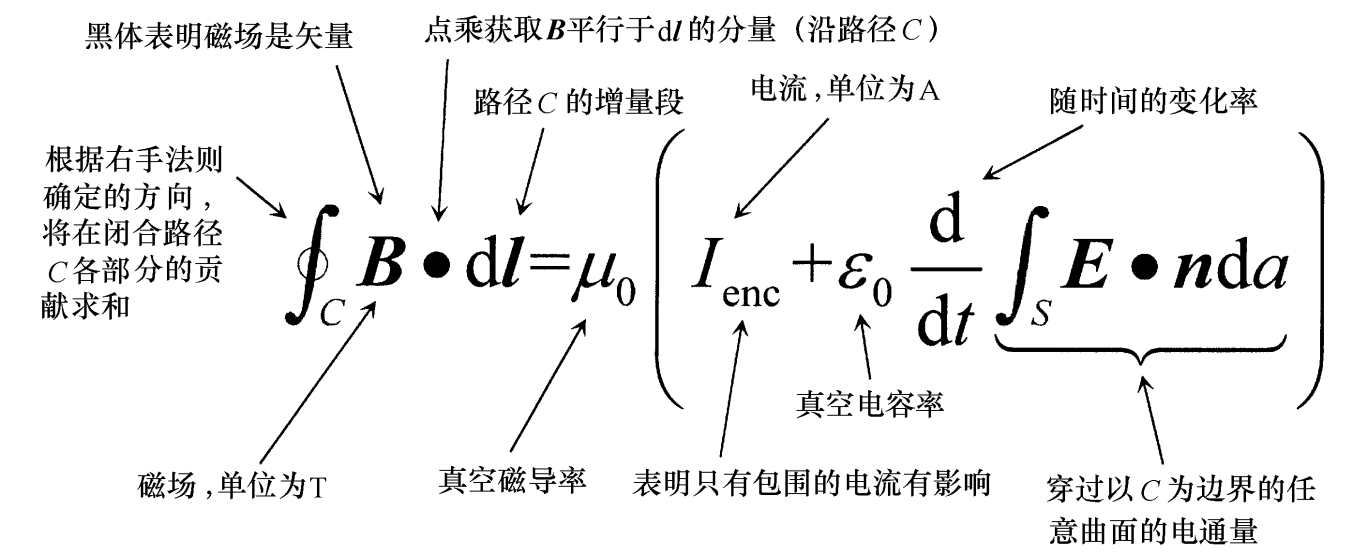
2.微分形式

电流和随着时间变化的电场会产生环绕的电场

洛伦兹力定律

电荷守恒定理

所有的电磁场可归因于电荷与电流，等式左边是输出，右边是输出

四、磁荷

理论物理学家为了对称性的美，期望磁荷的存在，并假设下式

但仍未被证实

五、介质中的麦克斯韦方程组

六、参考资料

总结

本文仅仅简单介绍了【物理学】电磁学——麦克斯韦方程组，评论区欢迎讨论。