DX_五角星计算

基础知识：
正五角星的角尖是36度，拐度是108度。

分析：

可以把五角星分成五个相同的等腰直接三角和一个正五边形，如图片。

多边形内角和计算公式：（n － 2）×180°(n大于等于3且n为整数）。

根据公式，可以算出五边形内角和为（5-2）×180°=540°，所以五边形每个角的度数为：540°÷5=108°。

已知正五边形每个角都是108° ，则等腰直角三角形的下面的两个相等的角为72°。

三角形内角和为180°，则三角形上面的那个角=180°-72°-72°=36°

所以，五角星的五个顶角各是36°，拐角度数=180-（180-36）÷2=108°。

五角星计算 ，确定坐标点：

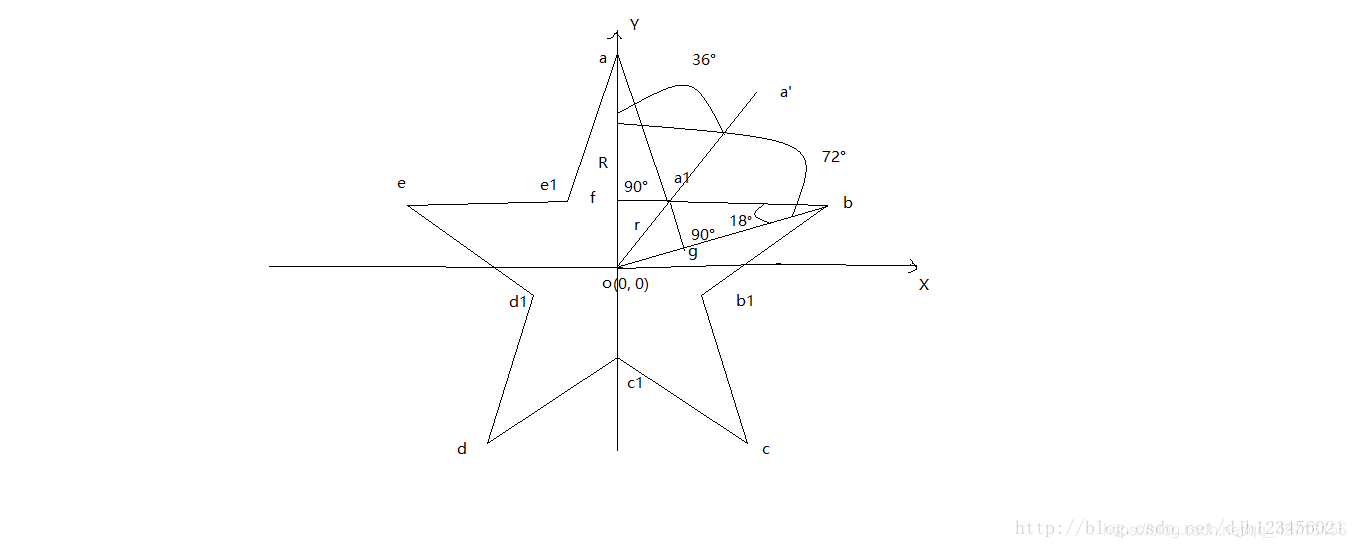
说明：
① 坐标原点o（0,0）为坐标原点
② 五角星的长轴为R = |oa|,长度已知
③ 五角星的短轴为r = |oa1|
④ 弧度制为rad = π/180 rad

五角星分为以下几个步骤：
① 求五角星外五个顶点的坐标（a,b, c, d, e）
由图可知：∠fbg = 18°,∠aoa’ = ∠a’ob = 36°, ∠aob = 72°
由极坐标公式：
x=rcos(θ),
x=rsin(θ),

可以得到外五角星的五个坐标：
（(R * cos(90°+ k * 72°+ yDegree)), (R * sin(90°+ k * 72°+ yDegree))）其中k = 0、1、2、3、4， yDegree为oa与y轴的夹角（如下图），默认为0。

但画图时会由中心点O（x， y）确定五角星外五个顶点的坐标，经过坐标变换为：

（x -(R * cos(90°+ k * 72°+ yDegree)), y - (R * sin(90°+ k * 72°+yDegree))）

②求解五角星内五顶点坐标(a1, b1, c1,d1, e1)

由图可知：r * cos(36°) = |fo| = R * sin(18°)

所以：r = R * sin(18°) / cos(36°);

根据步骤①相同方法得到五角星内五顶点坐标：
（(R* cos(90°+ 36°+ k * 72°+yDegree)), (R * sin(90°+ 36°+ k * 72°+yDegree))）其中k = 0、1、2、3、4， yDegree为oa与y轴的夹角，默认为0。

但画图时会由中心点O（x， y）确定五角星外五个顶点的坐标，经过坐标变换为：
（x -(R * cos(90°+ 36°+ k * 72°+yDegree)), y - (R * sin(90°+ 36°+ k* 72°+ yDegree))）

原文链接：计算机图形学-五角星的画法