数学建模 --- 预测性与解释性回归：多元线性回归用Stata分析

最新推荐文章于 2024-07-24 10:23:42 发布

星码

最新推荐文章于 2024-07-24 10:23:42 发布

阅读量1.5w

点赞数 34

分类专栏：数学建模文章标签： Stata 数学建模

本文链接：https://blog.csdn.net/qq_43779658/article/details/107896721

版权

数学建模专栏收录该内容

16 篇文章

订阅专栏

多元线性回归分析

回归分析
数据分类 --- 通过数据类别选择合适的建模方法
数据网站
线性回归 --- 横截面数据
Stata对数据描述性统计
求出的拟合优度 $R^2$ 较低时
- 拟合优度和调整后的拟合优度

回归分析

研究X与Y的相关性
在这里插入图片描述

X — 自变量， Y — 因变量
回归的分类

解释性回归
预测性回归

回归分析的任务
通过研究X和Y的相关关系，尝试去解释Y的形成机制，进而达到通过去预测Y的目的
使用目的

判断那些X是与Y真的相关
相关的X与Y是正相关还是负相关
不同X有不同的权重(不同的回归系数)，可以得到不同变量之间的相对重要性

回归分析的分类
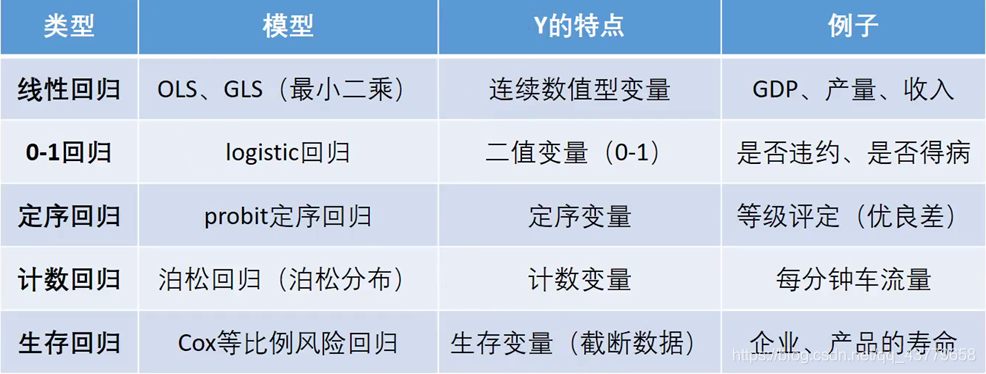
不同数据处理方法

数据分类 — 通过数据类别选择合适的建模方法

横截面数据 — 在某一时间点收集的不同对象的数据
比如：某年各省的GDP
时间序列数据 — 对统一对象在不同时间所得数据
比如：一个省每年的GDP
面板数据 — 横截面数据与时间序列数据综合起来
比如： 2008-2018，各省份GDP

数据网站

【简道云汇总】110+数据网站
 【汇总】数据来源/大数据平台
 大数据工具导航
 大数据查询导航

线性回归 — 横截面数据

对线性的理解

自变量和因变量可以通过变量变换而转化为线性模型
在这里插入图片描述

例如：将 $y_i=\beta_0+\beta_1lnx_i+\mu_i$ 中的 $lnx_i$ 用一个新变量进行替换

用新变量替换时求对应的值可以使用Excel

在这里插入图片描述

回归系数

回归系数解释

在这里插入图片描述

使用回归前，要检验扰动项是否满足某些条件 — 重点

多元线性回归扰动项满足的条件

扰动项 $\mu$ 的内生性

误差项 $\mu$ 与自变量 $x$ 相关
扰动项 $\mu$ 中包含了与 $y$ 有关但没有放到模型中的变量

在这里插入图片描述
1.对于扰动项 $\mu$ 满足一定的条件为：不存在内生性，不存在异方差
2. 例如：在仅有变量 $x$ 为产品品质时，会出现内生性

$\because$ 会有价钱也与 $y$ 有关，因为没有添加到模型中(即存在于 $\mu$ 中)，而价格于品质 $x$ 有关
$\therefore$ 产生了内生性
外生性很难满足
$\therefore$ 为了降低了条件 — 引入核心解释变量和控制变量

解决外生性 — 核心解释变量和控制变量

在这里插入图片描述仅仅保证核心解释变量与 $\mu$ 无关，而不用保证控制变量与 $\mu$ 无关
$\therefore$ 控制变量就是为了控制那些对核心解释变量影响的遗漏的变量(这些变量在 $\mu$ 中)

当式子中有对数时，对回归系数的解释

在这里插入图片描述

总结：四类模型回归系数的解释

在这里插入图片描述

多变量时

加一句：在控制其他自变量不变的情况下

变量

定性变量变为定量变量 — 引入虚拟变量

在这里插入图片描述

虚拟变量解释

例如研究性别与工资影响：
$y_i=\beta_0+\delta_0Female_i+\beta_1x_{1i}+\beta_2x_{2i}+...+\mu_i$

$Female_i =1$ ：表示第 $i$ 个样本为女性
$Female_i =0$ ：表示第 $i$ 个样本为男性
核心解释变量: $F e m a l e$
控制变量: $x_m(m=1,2,...k)$

设置虚拟变量

为了避免完全多重共线性的影响，引入虚拟变量的个数一般为分类数 - 1
比如：定性变量（男/女），有两个分类，所以设置一个虚拟变量
当出现完全多重共线性时，回归系数无法计算

含有交互项的自变量

因变量受到一个核心解释变量和另一个核心解释变量共同影响

在这里插入图片描述

在论文对变量解释介绍

在这里插入图片描述

一元线性回归

与一元线性函数拟合本质类似
仅有一个自变量

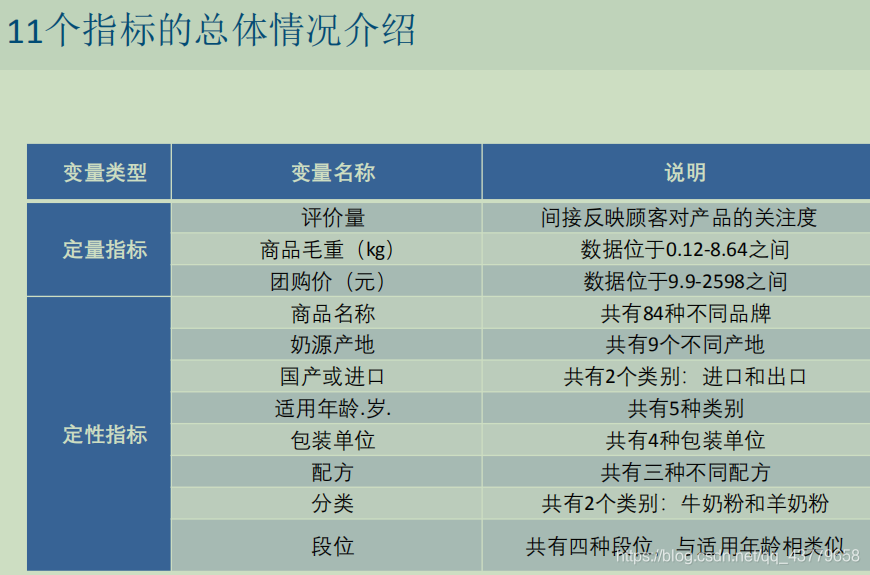
在这里插入图片描述

Stata对数据描述性统计

定量数据

summarize  变量1 变量2 ... 变量n

在这里插入图片描述

如果放入论文中，需要先放到Excel中，变成三线表，然后将三线表放到论文中

定性数据 — 生成虚拟变量

// 得到出现的次数(Freq)
tabulate 变量

该函数每次仅对一个变量进行分析

在这里插入图片描述

tab 变量 ,gen(A)

生成对应变量的虚拟变量 $A 1 . . . A n$

在这里插入图片描述

例如图中，有两种配方，有两个虚拟变量 $A 1, A 2$
当为第一种配方的时候， $A 1 = = 1; A 2 = = 0$
当为第二种配方的时候， $A 1 = = 0; A 2 = = 1$

Excel画出变量的频率扇形图

插入 -> 数据透视表
选择所需字段

可以选择值显示的方式(数字或百分比)
画出扇形图
分析 -> 数据透视图

在图中加入数字
为了让画出来的图有美感
可以先进行排序后再画开始 -> 排序
可以进行颜色的变更：页面布局 -> 颜色

Stata 回归 — 分析各个变量与因变量的关系

使用回归前，要检验扰动项是否满足某些条件 — 重点

多元线性回归扰动项满足的条件

对定量变量回归

regress y x1 x2 ...

在这里插入图片描述

Model: 代表SSR，回归平方和
Residual: 代表SSR，误差平方和
Total: 代表SST

上面三个对应的值在SS列中

R-squared: 代表 $R^2$ ，拟合优度
$0<=R^2<=1$
Adj R-squared: 代表调整后的拟合优度
df: 代表自由度

联合显著性检验 — $P r o b > F$ 的值看模型是否合理

$P r o b > F$ 对应的值要 $< 0.05$ ，否则模型设置不合理

在这里插入图片描述
检验回归系数使用的 $t$ 回归统计量

Coef: 估计出来的回归系数
cons: 常数项的估计值
最后一列为置信区间

分析的变量选择 — 回归系数显著

只需要分析回归系数显著的变量(看 $P > ∣ t ∣ 一列$ ,当值 $< 0.05$ 代表在 $95\%$ 置信水平下，回归系数显著异于 $0$ )

回归系数解释

在这里插入图片描述

在其他变量不变的情况下，团购价元每增加1，会导致评价量减少35.49873

对定性变量回归

使用tab 变量 ,gen(A)产生的虚拟变量 $A 1 . . . A n$
再使用regress y A1 A2 ...An

为了避免多重共线性的影响，会自动将某个虚拟变量设置为对照组

例如图中将G4看为对照组：
在这里插入图片描述

联合显著性检验 — $P r o b > F$ 的值看模型是否合理

$P r o b > F$ 对应的值要 $< 0.05$ ，否则模型设置不合理

图中含义：
在这里插入图片描述

检验回归系数使用的 $t$ 回归统计量

Coef: 估计出来的回归系数
cons: 常数项的估计值
最后一列为置信区间

分析的变量选择 — 回归系数显著

只需要分析回归系数显著的变量(看 $P > ∣ t ∣ 一列$ ,当值 $< 0.05$ 代表在 $95\%$ 置信水平下，回归系数显著异于0)

回归系数的解释

例如：
有四个段位，观察段位与评价量的关系

reg 评价量 G1 G2 G3 G4

在这里插入图片描述

解释回归系数：

G1回归系数（Coef对应的那列）
在控制其他变量不变的情况下，段位1与段位4比较，评价量相差 $- 7595.045$

Stata对回归分析结果用文档保存

regress 评价量 团购价元 商品毛重kg
// 下面的语句可帮助我们把回归结果保存在Word文档中
// 在使用之前需要运行下面这个代码来安装下这个功能包（运行一次之后就可以注释掉了）
// ssc install reg2docx, all replace
// 将模型保存为m1
est store m1
reg2docx m1 using m1.docx, replace
// *** p<0.01  ** p<0.05 * p<0.1