雷达原理---目标回波的频谱特性

最新推荐文章于 2024-04-12 16:22:10 发布

知知知_了

最新推荐文章于 2024-04-12 16:22:10 发布

阅读量6.7k

点赞数 4

分类专栏：雷达原理文章标签：矩形脉冲串 sinc函数天线扫描函数

本文链接：https://blog.csdn.net/qq_45732223/article/details/109744965

版权

雷达原理专栏收录该内容

16 篇文章

订阅专栏

1. 雷达回波信号的频谱

雷达回波信号：
$s_r(t)=ks_t(t-t_r)$
回波信号的频谱：
$S_r(f)=ks_t(f)e^{-j\omega t_r}$
可以看出，接收信号的幅频特性与发射信号的幅频特性是一样的，只不过接收信号的频谱高度有一定的衰减，但是形状是一样的。

因此，我们首先来分析发射信号的频谱特性

2. 无限长相干脉冲串的幅度谱

雷达发射相参脉冲串 $u (t)$ ，其脉冲宽度为 $\tau$ ，脉冲重复频率为 $f_r$
$\sum_{n=-∞}^{∞} rect(t-nT_r,\tau)cos(w_0t)$
式中， $E$ 为信号振幅
$rect(t,\tau)= \begin{cases} 1，|t|\leq \frac{\tau}{2} \\ 0，其它 \end{cases}$

周期化的门函数是通过傅里叶级数来讨论其傅里叶变换的，周期信号的频谱是离散谱，是一根根离散的 $\delta$ 函数，而 $\delta$ 函数之间的间隔等于周期信号周期的倒数，即 $\frac{1}{T_r}$ ，也就是雷达的脉冲重复频率 $f_r$ ，其幅度谱的包络为 $s i n c$ 函数形状。

考虑到 $cos(w_0t)=\frac{1}{2}(e^{jw_0}+e^{-jw_0})$ ，那么 $u (t)$ 的频谱就是将周期门函数的频谱搬到 $f_0$ 的位置处，且幅度下降了一半。

对于运动目标，接收信号的频率比发射信号的频率多了一个多普勒频移 $f_d$ ，此时 $u (t)$ 的频谱就是将周期门函数的频谱搬到 $f_0+f_d)$ 的位置处。

3. 有限长相干脉冲串的幅度谱

实际接收信号不可能是 $- \infty$ 到 $\infty$ ，接收信号必须超过雷达接收机的门限，接收信号什么时候超过门限与接收天线的天线方向图函数有关，当接收到的某一时刻的回波信号是从天线方向图函数的最大值的指向进去的时候，这个幅度就是最大的。

那么，实际接收信号为
$u_r(t)=s_r(t)m(t)$

其中， $m (t)$ 为天线扫描函数.

设天线方向图可用高斯函数表示
$m(t)=\sqrt{2}\pi \sigma e^{-2 \pi^2 \sigma^2 t^2}$
式中， $\sigma$ 是和天线波瓣宽度及扫描速度均有关的参数。 $\sigma$ 减小，表示观察的时间增加。

$m (t)$ 的频谱可求得为
$M(f)=e^{-f^2/(2\sigma^2)}$

天线扫描时实际回波信号的频谱
$U_r(f)=S_r(f)*M(f)=U(f)*M(f)$

可以这么理解，收到的回波不可能像发射的一样 $- \infty$ 到 $\infty$ ，因为天线方向图函数 $m (t)$ 乘以无限脉冲串，落在天线方向图里的脉冲个数为有限数。

$U (f)$ 是 $\delta$ 函数，与 $M (f)$ 做卷积，相当于把 $\delta$ 函数的位置换成 $M (f)$ 的波形，也就是说 $U_r(f)$ 的频谱为无限回波脉冲串频谱 $U (f)$ 的每一根谱线均按 $M (f)$ 的形状展宽。

4. MATLAB仿真

代码：

close all;
clear all;
clc;
%%*************** 目标回波的频谱特性 ***************%%

% 信号参数设置
E   = 1;                % E  : 信号振幅
tau = 2;                % tau: 信号时宽
number = 5;             % 矩形脉冲个数
Fs  =  1000;            % 采样率
PRT = 5*tau;            % 脉冲重复周期
N1  = round( tau*Fs );  % 信号时宽内的采样点数
N   = round( PRT*Fs );  % 一个脉冲重复周期内的采样点数

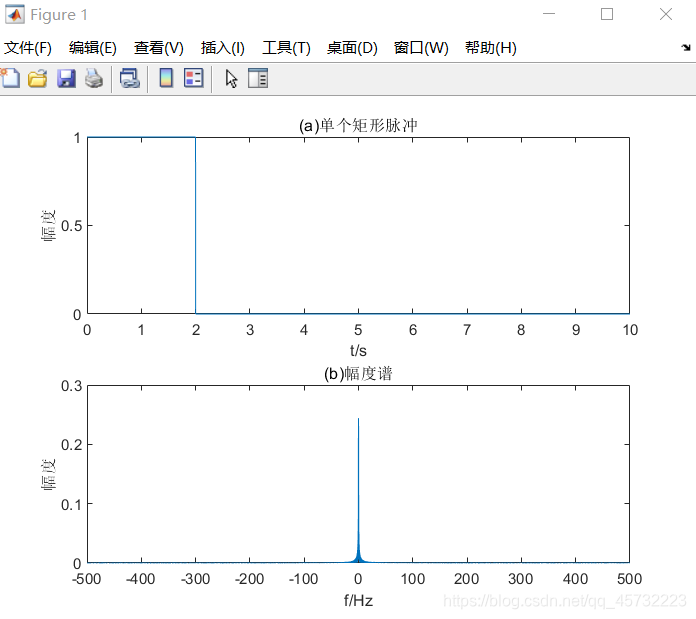
% 单个矩形脉冲：频谱函数为sinc函数
s1 = zeros(1, N);
t1 = linspace(0, PRT , N);
s1 = ( abs(t1) < tau ) .*E; 

L1 = 2^nextpow2(N);
f1 = linspace(-Fs/2, Fs/2, L1);
S1 = fftshift( abs( 2*fft(s1,L1)./L1 ));

figure;
subplot(2,1,1); plot(t1 ,s1); xlabel('t/s'); ylabel('幅度'); title('(a)单个矩形脉冲');
subplot(2,1,2); plot(f1,S1); xlabel('f/Hz'); ylabel('幅度'); title('(b)幅度谱');

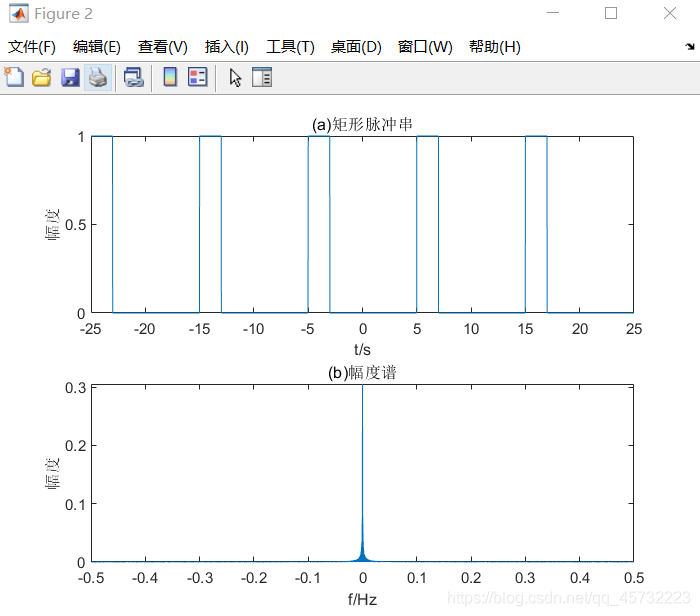
% 无限长矩形脉冲串：频谱函数为离散的δ谱线，包络为sinc函数
N_all = PRT * number * Fs;      % 所有矩形脉冲的采样点数
t2 = (-N_all/2:N_all/2-1)/Fs;
s2 = zeros(1,N_all);            % 初始化所有值为零
for i=1:number
    s2((i-1)*N+(1:N))= s1;
end

L2 = 2^nextpow2(N_all);
f2 = linspace(-PRT*number*Fs/(2*N_all) ,PRT*number*Fs/(2*N_all) ,L2);
S2 = fftshift( abs( 2*fft(s2,L2)./L2 ));

figure;
subplot(2,1,1); plot(t2 ,s2); xlabel('t/s'); ylabel('幅度'); title('(a)矩形脉冲串');
subplot(2,1,2); plot(f2,S2); xlabel('f/Hz'); ylabel('幅度'); title('(b)幅度谱');

% 高斯型天线扫描函数：其频谱函数依然为高斯型
delta=0.05;
m=sqrt(2)*pi*delta*exp(-2*(pi^2)*(delta^2).*(t2.^2));
M = fftshift( abs( 2*fft(m,L2)./L2 ));

figure; 
subplot(2,1,1); plot(t2 ,m ); xlabel('t/s'); ylabel('幅度'); title('高斯型天线扫描函数');
subplot(2,1,2); plot(f2,M); xlabel('f/Hz'); ylabel('幅度'); title('高斯型天线扫描函数幅度谱');

% 天线扫描时回波信号的频谱图
Sr = xcorr(S2,M);
figure;plot(Sr); title('目标回波的频谱特性');

结果：