【超详细】VLN算法学习：AZHP——使用自适应区域分层规划器来实现层次化导航的目的Adaptive Zone-aware Hierarchical Planner for VLN

【VLN入门介绍】

一文搞懂视觉语言导航，从任务介绍到基本算法讲解：https://blog.csdn.net/qq_50001789/article/details/144676313

【VLN算法笔记】

DUET（CVPR2022），首篇使用Transformer来建模全局图节点相关性的工作：https://blog.csdn.net/qq_50001789/article/details/144632851
AZHP（CVPR2023），使用自适应区域分层规划器来实现层次化导航的目的：https://blog.csdn.net/qq_50001789/article/details/144635128
GridMM（ICCV2023），使用网格记忆图来表征历史轨迹中的场景空间关系：https://blog.csdn.net/qq_50001789/article/details/144652403

【VLN辅助任务】

MLM、SAP、SAR、SPREL——预训练、微调中常用的提点策略：https://blog.csdn.net/qq_50001789/article/details/144633984

【VLN环境配置】

Matterport3DSimulator——用于视觉语言导航算法研发的仿真环境配置：https://blog.csdn.net/qq_50001789/article/details/142621259

综述

论文题目：《Adaptive Zone-aware Hierarchical Planner for Vision-Language Navigation》

论文链接：http://openaccess.thecvf.com/content/CVPR2023/papers/Gao_Adaptive_Zone-Aware_Hierarchical_Planner_for_Vision-Language_Navigation_CVPR_2023_paper.pdf

源码链接：https://github.com/chengaopro/AZHP

论文出处：CVPR 2023、刘偲老师团队

关键词：分层导航

背景

  VLN给定的指令往往具有层次性，比如一个指令“Bring me the white pillow"（给我一个白色枕头），这表明智能体需要完成几个潜在的子目标，例如：离开当前房间、找到卧室、找到白色枕头。因此，VLN任务本质上是一种分层导航的过程，我们可以在导航的过程中设置多个子目标，之后逐一完成所有的子目标导航任务，进一步完成整个导航任务，在本文中，子目标的划分称为高阶任务，子目标的执行称为低阶任务。其次，子目标是指一个子区域内的目标，因此需要智能体可以将场景划分为几个区域，并为当前的子目标选择合适的区域，在子区域中执行低阶的动作规划。注意：子目标的选择不仅取决于指令，还需要智能体根据当前的状态环境来设置合适的子目标，这意味着智能体在导航过程中需要自适应地进行区域的划分和选择。例如在下图中，当智能体在客厅时，子目标应该设置为：在出口区域（红色区域）找到出口。第三，由于子目标的设置是没有标签的（无法使用模范学习来优化这一过程），因此如何学习这一高阶策略网络也是一个值得研究的课题。

  当前主流的VLN算法主要为单步规划方法本质上都是单步规划框架，每次根据动作空间和全局目标直接执行一步导航操作，这种范式没有明确地模拟VLN任务的分层规划特性，很大程度上限制了长期决策能力。

主要思想

  本文提出了一种自适应区域感知分层规划器（Adaptive Zone-aware Hierarchical Planner, AZHP），为VLN任务构建一种新的分层规划框架。AZHP将导航过程建模为包含高阶动作和低阶动作的分层动作制定过程，在导航过程中，高阶动作的目标是设置子目标，低阶动作的目标是完成相应的子目标。具体地来说，高阶动作将整个场景划分为不同的区域，并根据当前状态选择合适的区域进行导航，例如图1©中的绿色区域（走廊），之后应用低阶动作在选定的区域内多步执行特定的导航决策，直至到达子目标。
  针对高阶动作的预测，作者提出了一种场景自适应感知区域划分方法（Scene-aware adaptive Zone Partition, SZP）。本文的方法是基于DUET算法来实现的，在该算法中，每执行一步动作，都会更新一次全局拓扑图，全局拓扑图记录了历史轨迹和观测结果，在此基础上，作者根据每个视点的位置和观测值，动态地将全局拓扑图自适应地划分为多个区域。同时，作者设计了一种目标导向的区域选择方法（Goal-oriented Zone Selection, GZS），根据指令和区域属性来选择特定的区域当做下一个子目标区域。此外，作者还设计了状态切换模块（State-Switcher Module, SSM）来判断当前子目标是否已经实现，如果已经实现就切换到下一个子目标。
  由于高阶动作的训练没有直接的标签进行监督，作者提出了分层强化学习（Hierarchical Reinforcement Learning, HRL）来优化这一高阶过程。

补充：本文的分层导航相当于对整个导航任务做一个解耦，想要直接完成整个导航任务是比较困难的，因为一条完整的路径比较长，中途的噪声干扰会给整个导航任务带来非常大的不确定性。对导航任务做解耦，将一个复杂的任务拆解成多个简单的子任务，逐一完成简单的子任务，最终实现复杂的导航目标，是VLN任务中非常常见的算法优化策略，而本文中是在轨迹区域层面实现解耦目的。

方法

分层规划概述

  VLN任务具有分层特性，它由一个高阶过程（即子目标的设置）和一个低阶过程（即子目标的执行）组成，子目标（sub-goal）是指到达一个子区域（sub-region）的目标。本文提出了一个自适应区域感知的分层规划器（Adaptive Zone-aware Hierarchical Planner, AZHP）来建模这一分层规划的过程，具体地来说，AZHP由两个策略网络组成，具体如下图所示。其中，高阶策略${\pi }^H(\cdot )$学习设置子目标$g^H$，低阶策略${\pi }^L(\cdot )$相应地学习实现$g^H$。在导航过程中，每执行一步观测，都会利用DUET算法中的策略来记录历史轨迹和当前观测值，生成全局的拓扑图$G_t$。

​  具体地来说，在时间步$t$时，利用学习到的高阶策略网络${\pi }^H(a_t^H|G_t;{\theta }^H)$来获得$a_t^H$（例如区域划分、区域选择），其中${\theta }^H$为网络的参数。经过区域划分和选择后，会得到一组选定的区域$G_t^{\ast }$，其中$G_t^{\ast }$为$G_t$的子图。之后分多步利用低阶策略网络${\pi }^L(a_t^L|G_t^{\ast };{\theta }^L)$得到低阶动作$a_t^L$，也就是导航决策，智能体只在子图$G_t^{\ast }$中导航决策，最后，作者提出了一个状态切换模型（State-Switcher Module, SSM）来学习子目标$g^H$是否达到，并且在导航中是否切换到下一个子目标。

分层强化学习

  由于没有用于训练高阶策略${\pi }^H(\cdot )$的专家演示（标签），作者在这里提出了一种分层强化学习策略来优化该网络。首先，作者设计了一个低阶策略的奖励函数${\pi }^L(\cdot )$，在第$t$步导航中，智能体会执行一个低阶动作$a_t^L$，奖励$r_t^L$定义为：

• 当离目标位置的距离$di{s}_t$发生变化时，当前步骤的奖励为：$r_t^L=-(di{s}_t-di{s}_{t-1})$；
• 当智能体停在目标位置时，当前步骤的奖励为：$r_t=10$，否则为$-10$；
• 当智能体路过目标位置但是不停止时，当前步骤的奖励为：$r_t=-10$；

之后通过累加所有的奖励，得到高阶策略的奖励：
$$r_t^H=\sum _{t=start}^{end}{r}_t^L$$
其中，$[start,end]$是当前子目标的时间段。

  之后采用时序差分算法（Temporal Difference algorithm, TD）来优化两个策略网络（基于$r_t^H$和$r_t^L$），以高阶策略的优化过程为例。技术上，利用MLP网络来构建状态价值评估函数$v^H(G_t;W^H)$，用于预测每个状态的价值量$v^H$，其中$W^H$是可学习的参数。状态价值函数用于评估当前状态的好坏，之后计算TD目标$y_t^H$和误差${\delta }_t^H$：
$$\begin{gathered} y_t^H=r_t^H+\gamma \cdot v^H(G_{t+1};W^H) \\ {\delta }_t^H=v^H(G_t;W^H)-y_t^H \end{gathered}$$
其中$\gamma$为收益因子，最后${\pi }^H(\cdot )$和$v^H(\cdot )$可以通过梯度下降法来优化：
$$\begin{gathered} {\theta }^H\leftarrow {\theta }^H-\beta \cdot {\delta }_t^H\cdot \frac{\partial }{\partial {\theta }^H}\ln ({\pi }^H(a_t^H|G_t;{\theta }^H)), \\ {W}^H\leftarrow W^H-\alpha \cdot {\delta }_t^H\cdot \frac{\partial }{\partial W^H}\ln (v^H(G_t;W^H)), \end{gathered}$$
其中$\alpha$和$\beta$是超参数。对于优化$W^H$，是朝着降低误差${\delta }_t^H$的方向进行，也就是让状态价值评估函数在评估状态价值方面越来越准。

高阶策略

​  为了自适应地为子目标设置子区域，作者提出了一种高阶策略网络，该网络包括场景感知的自适应区域划分（Scene-aware adaptive Zone Partition, SZP）和目标导向的区域选择（Goal-oriented Zone Selection, GZS）。

场景感知的自适应区域划分（SZP）

​  在时间步长$t$处，作者在当前的视角图中应用目标检测器来提取目标级别的视觉特征，之后参考DUET算法，采用跨模态Transformer来将当前视角/目标的视觉语言特征融入拓扑图$G_t=(H_t,E_t)$中，$G_t$包括$N_t^v$个节点，其中$H_t\in {\mathbb{R}}^{N_t^v\times D_h},E_t\in {\mathbb{R}}^{N_t^v\times N_t^v}$分别表示节点特征矩阵和加权邻接矩阵，$E_t$初始化为相应视点之间的距离。SZP的目标是在$G_t$上进行分区，得到一组子视图${G_t^i}_{i=1}^{N_t^z}$，其中$N_t^z$表示分区序号。本算法在导航过程中自适应设置$N_t^z$，$G_t$越大，对应划分的区域就应该越多，计算公式为：
$$N_t^z=\lceil visit\_le{n}_t\times ratio\rceil$$
其中$visit\_le{n}_t$表示当前轨迹的长度，$ratio\in (0,1)$为超参数。

​  对于区域的划分，首先将所有的节点视为区域中心（zone centre），目标是为每个节点生成对应区域的特征 Z t = { z t i } i = 1 N t v Z_t=\{z^i_t\}_{i=1}^{N^v_t} Zt​={zti​}i=1Ntv​​（具体见图3中的（a）子图），考虑到$z_t^i$应该代表其周围的状态，本算法以一种自适应的方式融合领域特征，具体地来说，我们计算节点特征$h_t^j\in {\mathbb{R}}^{1\times D_h}$对节点特征$h_t^i\in {\mathbb{R}}^{1\times D_h}$，的关系分数$s_t^{i,j}$：
$$s_t^{i,j}=\{\begin{array}{ll}\sigma ([h_t^i{W}_H,h_t^j]W_S)& e_t^{i,j}<TH{R}_d\\ -\inf & \text{else}\end{array}$$
其中$\sigma (\cdot )$为激活函数，$[,]$为拼接操作，$W_H\in {\mathbb{R}}^{D_h\times D_h}$和$W_S\in {\mathbb{R}}^{2D_h\times 1}$分别为可学习的参数，$e_t^{i,j}$为节点$i$和节点$j$之间的距离，预设一个距离阈值$TH{R}_d$，当节点之间的距离超过阈值时，我们认为该节点不是相邻关系，经过上述运算之后，会得到关系分数矩阵$S_t\in {\mathbb{R}}^{N_t^v\times N_t^v}$，之后再经过softmax运算对关系分数矩阵做标准化操作，具体过程可以表示为$S_t\leftarrow softmax(S_t)$，之后通过$Z_t=S_t{H}_t$得到区域特征，即关系分数矩阵和节点特征矩阵相乘。

  其次，如图3(b)所示，通过计算节点$i$的代表性得分${\varphi }_t^i$，我们对区域特征$z_t^i$进行分级：
$${\varphi }_t^i=\sigma (z_t^i{W}_1+\sum (z_t^i{W}_2-z_t^j{W}_3)),e_t^{i,j}<TH{R}_d$$
其中$W_1,W_2,W_3\in {\mathbb{R}}^{D_h\times 1}$为可学习的参数，$(z_t^i{W}_2-z_t^j{W}_3)$表示两个区域之间的差异线索，由于我们预计将$G_t$划分为$N_t^z$个子区域，因此我们根据${\varphi }_t$选择分数最高的前$N_t^z$个区域中心，我们将区域中心的索引表示为${\hat{i}}_t$，因此区域内节点的概率分布为$P_t=softma{x}_{{\hat{i}}_t}(S_t)\in {\mathbb{R}}^{N_t^v\times N_t^z}$（每个区域在内部做一次归一化操作），之后根据$P_t$和距离将其他节点分配到选定的区域中心（具体如图3©所示）。因此，我们将$G_t$划分为$N_t^z$个子区域 { G t i } i = 1 N t z \{G^i_t\}^{N^z_t}_{i=1} {Gti​}i=1Ntz​​，其中$G_t^i=(H_t^i,E_t^i)$，$H_t^i$和$E_t^i$分别表示第$i$个区域内的节点特征和邻接矩阵。

目标导向的区域选择（GZS）

​  本模块用于从 { G t i } i = 1 N t z \{G^i_t\}^{N^z_t}_{i=1} {Gti​}i=1Ntz​​中选择一个区域$G_t^{\ast }$来进行进一步的低阶导航操作。首先，利用文本编码器对语言指令进行编码，得到文本编码特征$I\in {\mathbb{R}}^{L\times D_h}$，其中$L$为语言指令长度。我们将生成的指令的句子级特征表示为$\hat{I}\in {\mathbb{R}}^{1\times D_h}$（这是什么意思？加个上标是什么意思，再看一下论文）。从本质上来说，我们希望所筛选的子目标区域是以指令为导向的，因此，如图3(d)所示，我们通过内部生产函数为每个区域计算一个区域分数：
$$zone\_scor{e}_i=\sigma (\hat{I}{W}_I)\cdot \sigma (z_t^i{W}_Z{)}^T$$
其中，$W_I,W_Z\in {\mathbb{R}}^{D_h\times D_w}$为可学习的参数。因此，我们选择得分最高的区域$G_t^{\ast }=(H_t^{\ast },E_t^{\ast })$当做当前子目标的导航区域，其中$N_t^{\ast }$为节点数，$H_t^{\ast }$和$E_t^{\ast }$分别为节点特征和邻接矩阵。选择完子区域之后，智能体沿着最短的路径移动到选定的区域中心，并在区域内执行后续的低阶动作预测。

低阶策略

导航决策

​  在时间步长为$t$时，低阶策略网络${\pi }^L(\cdot )$产生低阶动作$a_t^L$（即导航决策）。具体地来说，只有当前区域$G_t^{\ast }=(H_t^{\ast },E_t^{\ast })$中的视点才能作为导航动作。我们采用多层交叉注意力来对$G_t^{\ast }$中的每个节点特征$h_t^{\ast i}$进行评估，并选择得分最高的视点$a_t^L$作为导航目标，过程可以表示为：
$$a_t^L=arg\underset{i\in G_t^{\ast }}{\max }CorssAttention(h_t^{\ast i},I)$$
这里具体的节点动作预测过程可以参考DUET算法。

状态切换模块（SSM）

​  为了确定是否将当前状态切换到下一个子目标，即应用另一组高阶和低阶动作，作者在这里提出了SSM。具体地来说，我们对时间步$t$处的状态分数做评估：
$$state\_scor{e}_t=\text{sigmoid}(\sigma (\hat{I}{W}_I^{\prime })\cdot \sigma (h_t^c{W}_S))$$
其中$h_i^c\in {\mathbb{R}}^{1\times D_h}$为当前视点的特征，$W_I^{\prime },W_S\in {\mathbb{R}}^{D_h\times D_w}$为可学习的参数。然后，我们为状态分数设置阈值$TH{R}_S\in [0,1]$，用于判断是否切换到下一个子目标，即是否重新划分整个图$G$并重新选择$G^{\ast }$进行导航，如果智能体保持当前子目标，它将通过低级动作继续在当前区域中进行导航，并将新观察到的视点添加到当前区域的图结构$G_t^{\ast }$以进行更新。

训练目标

  训练损失主要包括两部分：高阶策略网络的辅助损失和低阶策略网络的行动损失。

辅助损失

​  对于高阶动作，作者采用分层强化学习和辅助损失来训练高阶策略网络，辅助损失包括区域划分损失$L_{zp}$和区域选择损失$L_{zs}$。对于$L_{zp}$，我们用启发式的方法划分$G_t$，并将结果作为分区标签，具体地来说，作者通过公式得到$N_t^z$区域的中心索引${\overline{i}}_t$：
i ‾ t = { r o u n d ( 1 + ( k − 0.5 ) × s t e p t ) ∣ k = 1 , … , N t z } \overline{i}_t=\{round(1+(k-0.5)\times step_t)|k=1,\dots,N^z_t\} it​={round(1+(k−0.5)×stept​)∣k=1,…,Ntz​}
其中，$round(\cdot )$表示四舍五入函数，$ste{p}_t=(visit\_le{n}_t-1)/N_t^z$，${\overline{i}}_t^k$表示第$k$个区域中心的索引，该运算过程会使区域中心分布均匀。之后通过最近邻搜索算法来计算节点$j$的区域标签${\overline{z}}_t^j$：
$${\overline{z}}_t^j=\arg \underset{i\in {\overline{i}}_t}{\min }{e}_t^{i,j}$$
此外，节点属于该分区的概率分布为$P_t$，其中$P_t(i,j)$为节点$j$属于分区$i$的可能性，$L_{zp}$的计算过程可以表示为：
$$L_{zp}=\sum _{t=1}^T\sum _{j=1}^{N_t^v}-\log P_t(j,{\overline{z}}_t^j)$$
​  对于$L_{zs}$，在时间步$t$时，我们取${\overline{i}}_t^{\ast }$为标签，其中${\overline{i}}_t^{\ast }$为标签GT视点所在区域的索引号：
$$L_{zs}=\sum _{t=1}^T-\log [softmax(zone\_score){]}_{{\overline{i}}_t^{\ast }}$$
课程学习策略：由于所提出的$L_{zp}$和$L_{zs}$不基于GT标签，仅提供启发式监督，因此，我们在训练阶段开始时应用它们以提高初始学习的鲁棒性。之后，我们利用HRL对网络进行训练，旨在获得更灵活的高层策略。

行动损失：这一模块主要用低阶的导航动作损失来计算：
$$L_{nav}=-\sum _{t=1}^T[\log p({\overline{a}}_t)+\log p({\overline{a}}_t^{\pi })]$$
其中${\overline{a}}_t$为教师动作，${\overline{a}}_t^{\pi }$为启发式动作标签（例如：从当前节点到目标节点的最短路径）。另外再采用$L_{og}=-\log p(\overline{o})$作为object grounding损失，其中$\overline{o}$为真实的对象。因此，总损失可以表示为：
$$L={\lambda }_1{L}_{zp}+{\lambda }_2{L}_{zs}+{\lambda }_3{L}_{nav}+L_{og}$$

补充：该算法同样分为预训练和微调两个阶段，具体用到的辅助损失与DUET中使用的相同。

实验结果

REVERIE数据集

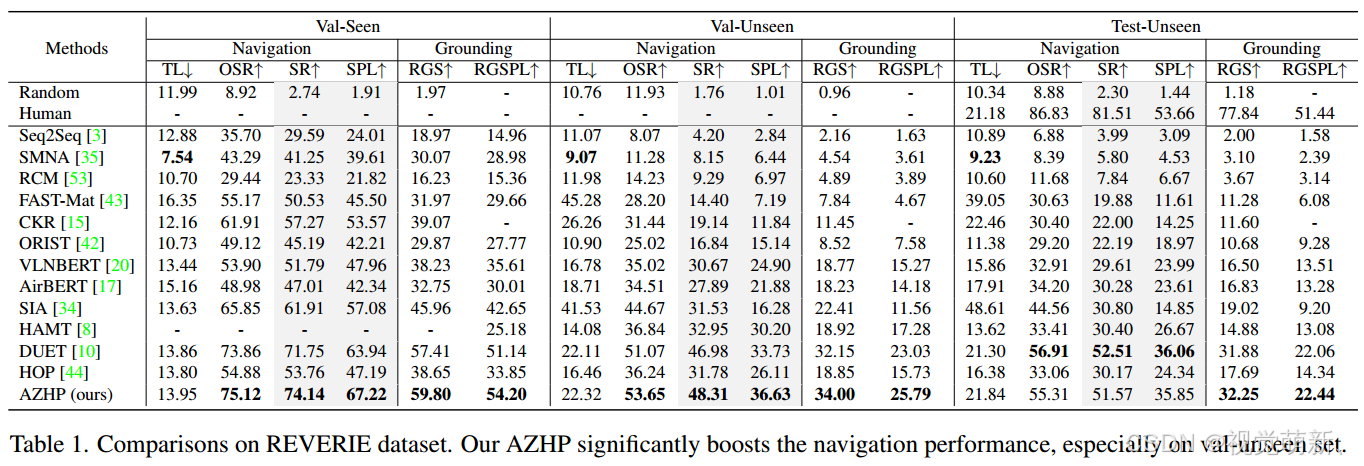
R2R数据集

以上仅是笔者个人见解，若有问题，欢迎指正。