线性代数——理解向（4）

最新推荐文章于 2025-01-17 10:22:07 发布

小小老大MUTA️

最新推荐文章于 2025-01-17 10:22:07 发布

阅读量3.5k

点赞数 2

分类专栏：线性代数文章标签：线性代数开发语言

本文链接：https://blog.csdn.net/qq_50645064/article/details/126798637

版权

线性代数专栏收录该内容

6 篇文章

订阅专栏

本文深入探讨了线性代数中的核心概念，包括矩阵行列式与体积的关系、特征值和特征向量的定义及性质。通过实例解析了特征值如何反映矩阵的伸缩和旋转效应，并介绍了矩阵对角化的过程及其在计算矩阵幂中的应用。此外，还提及了复数特征值、重特征值以及如何处理它们。内容涵盖矩阵的迹、对称矩阵的特征向量正交性以及退化矩阵的情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

麻省理工学院 - MIT - 线性代数（我愿称之为线性代数教程天花板）_哔哩哔哩_bilibili

MIT—线性代数笔记00 - 知乎 (zhihu.com)

行列式的部分相关性质与知识点这里暂不描述，可看上面给出的知乎笔记

一、行列式与体积之间的关系

矩阵A行列式的绝对值等于以矩阵A行（列）向量为边所构成的平行六面体的体积。行列式的正负对应左手系和右手系。

如果矩阵A是单位矩阵，则其构成的是三个边长均为1且互相垂直的立方体，其体积为1，这与上面的结论相符

而如果矩阵A为正交矩阵Q，则其构成的也是三个边边长为1且三边互相垂直的立方体，其体积也为1只是取向与单位阵不同。这也与上面的结论相符，因为 $Q^{T}Q=I$ ，且 det(Q)=det(QT) ，所以detQ=1。

交换矩阵A中的行并不会改变其行列式的绝对值，显然也不会改变向量围成的体积，因此这也和体积理论相符。

二、特征值和特征向量

如何通俗地解释特征值与特征向量_哔哩哔哩_bilibili（非常有助理解）

矩阵A完成的是一个向量空间到另一个向量空间的映射，有些向量映射前后在一条直线上，该向量称为特征向量。这里的矩阵A就只起到了伸缩作用，因此可以表示为 $\lambda$ ，称为特征值；

非零x满足 $Ax=\lambda x$ , $\lambda$ 就被称为A的特征值，x称为A的对应于特征值 $\lambda$ 的特征向量；

举例：求 $A=\begin{bmatrix} -1 & 0\\ 0&1 \end{bmatrix}$ 的特征值，特征向量：

$Ax=\lambda x\rightarrow (A-\lambda I)x=0$ ;

如果方程有非零解，那么系数矩阵为奇异矩阵，行列式为零，求出 $\lambda$ 的值，分别带入方程，求出方程的解

迹

迹是对角线所有元素的和；

矩阵的迹等于特征值之和；

对称矩阵的特征向量正交；

特征值之积等于行列式；

复数特征值

$Q=\begin{bmatrix} 0 &-1 \\ 1& 0 \end{bmatrix}=\begin{bmatrix} cos90^{\circ} & -sin90^{\circ}\\ sin90^{\circ} & cos90^{\circ} \end{bmatrix}$ 是一个90°的旋转矩阵，从矩阵的迹和行列式的值可以得到 $\lambda _{1}+\lambda _{2}=0$ ,所以两个数一正一负； $\lambda _{1}\lambda _{2}=1$ 所以两个数同符号，综上无解。从矩阵的性质可知它的实数特征向量只有零向量，因为其他任何向量乘以旋转矩阵，向量的方向都会发生改变。计算可得：

可以解得λ1=i 和 λ2=−i 。如果一个矩阵具有复数特征值a+bi则，它的共轭复数a-bi也是矩阵的特征值。实数特征值让特征向量伸缩而虚数让其旋转。

三角阵和重特征值

对于 $A=\begin{bmatrix} 3 &1 \\ 0 &3 \end{bmatrix}$ 的三角矩阵，特征值就是矩阵对角线上的元素；

说明A是一个退化矩阵，对应相同的特征值而特征向量短缺；

四、对角化和矩阵的幂

对角化矩阵

如果矩阵A具有n个线性无关的特征向量，将他们作为列向量可以组成一个可逆方阵S，并且有：

这里的矩阵 $\wedge$ 为对角阵，他的非零元素就是矩阵A的特征值。因为举证S中的列向量线性无关，因此逆矩阵 $S^{-1}$ 存在。在等是两侧左乘逆矩阵，得到 $S^{-1}AS=\wedge$ ,同样 $A=S\wedge S^{-1}$ 。

现在我们得到的是矩阵的”相似标准型“，它还保留来了矩阵操作的基本性质——特征值；

而之前的消元行操作和列操作得到的”相抵标准型“，之神下最内核的秩；

矩阵的幂

如果矩阵A具有n个线性无关的特征向量，如果所有的特征值均满足 $\left | \lambda _{i} \right |< 1$ ,则 $k\rightarrow \propto$ 时， $A^{k}\rightarrow 0$ .

重特征值

如果矩阵A没有重特征值，则其一定具有n个线性无关的特征向量。

如果矩阵A有重特征值，它有可能具有n个线性无关的特征向量，也可能没有。比如单位阵的特征值为重特征值1，但是其具有n个线性无关的特征向量。

差分方程

用斐波那契数列举例：

为了凑成矩阵形式，列以下方程组：

令 $u_{k}=\begin{bmatrix} F_{k+2}\\ F_{k+1} \end{bmatrix}$ ,则有 $u_{k+1}=\begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}u_{k}$ ,观察矩阵 $A=\begin{bmatrix} 1 &1 \\ 1 & 0 \end{bmatrix}$ 的特征向量和特征值，因为是对称矩阵，特征值为实数，特征向量正交；

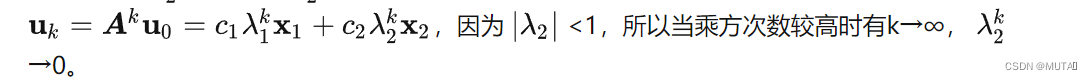
求解方程，这里使用小技巧：

$(A-\lambda I)x=0\rightarrow \begin{bmatrix} 1-\lambda & 1\\ 1& -\lambda \end{bmatrix}x=0$ ，求非零解，那么左边是奇异矩阵，所以行向量线性相关，用系数矩阵第二行乘以x的结果和第一行相同，而可以一眼第二行乘x=0， $x=\begin{bmatrix} \lambda \\ 1 \end{bmatrix}$