【算法系列】终于有人把隐马尔可夫链的前向后向算法讲懂了！

前言

视频讲解在我女朋友的B站『终于有人把隐马尔可夫链的前向后向算法讲懂了！』

在上一篇文章《你真的理解隐马尔可夫模型了吗？》中，我们讲解了隐马尔科夫链中的基本概念，并在最后说明了隐马尔可夫链中三个基本问题：

1. 概率计算问题：给定模型参数$\lambda =(A,B,\pi )$和观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_1,x_2,...,x_n\} x={x1​,x2​,...,xn​}计算在模型参数$\lambda$下观测到x的概率$P(x|\lambda )$(评估模型和观测序列之间的匹配程度)

2. 预测问题：给定模型$\lambda =(A,B,\pi )$和观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_1,x_2,...,x_n\} x={x1​,x2​,...,xn​}，求使得$P(y|x,\lambda )$最大的状态观测序列 y = { y 1 , y 2 , . . . , y n } y=\{y_1,y_2,...,y_n\} y={y1​,y2​,...,yn​}(根据观测序列推断最有可能的状态序列)

3. 学习问题：给定观测序列 x = { x 1 , x 2 , . . . , x n } x=\{x_1,x_2,...,x_n\} x={x1​,x2​,...,xn​}，调整模型参数$\lambda =(A,B,\pi )$，使得该序列出现的概率$P(x|\lambda )$最大(训练模型使其更好地描述观测序列)

这篇文章将会以尽可能通俗易懂的方式为大家讲解这几个问题的解法，其中概率计算问题将主要讲解前向、后向算法，预测问题将主要讲解维特比算法，学习问题主要讲解神经网络学习的方式。

1.直接计算法

直接计算法就是枚举所有的路径，然后将所有路径求和，得到最终答案，这种计算方法计算复杂度为$O(n{N}^m)$(每条路经有2n个乘法操作，共$N^n$个路径)，计算过程复杂，且耗时，我们仅列举一下计算方法，不过多解释：

2.前向算法

我们使用这样一个信封抽球问题作为例子讲解，状态为第0/1号信封，观测为球的颜色为红/黑

我们先不管观测到的5个状态，就假设观测到了第一个球为红色，这个概率该怎么计算呢？

我们不知道第一个状态是哪个信封，我们只能根据一些先验去猜：有两种可能状态0/1，可能得到红球，如果第一个状态为0，那么得到红球观测的概率为$B_{00}$,如果第一个状态为1，那么得到红球观测的概率为$B_{10}$。

而这里我们用来猜的的先验就是稳态向量$\pi$，我们拿到这个稳态向量可能会猜，是0的概率为0.5，是1的概率为0.5,那么:

• 如果第一个状态为0，得到观测为红球的概率就是$P=\pi (0)B_{00}$
• 如果第一个状态为1，得到观测为红球的概率就是$P=\pi (1)B_{10}$

然后将二者加起来就可以得到第一个观测为红球的概率$P(x_1|\lambda )=\pi (0)B_{00}\ast \pi (1)B_{10}$

我们将$P=\pi (0)B_{00}$记为${\alpha }_1(0)$，这表示第1个状态(下标)为0(值)的概率；同样将$P=\pi (1)B_{10}$记为${\alpha }_1(1)$，这表示第1个状态(下标)为1(值)的概率，这样表示是因为后面计算我们会用到，以简化我们的计算量。

我们再加入进来一个状态–$x_2=黑$，我们采用同样的方法，得到第二个观测为黑球，也只有两种可能状态0/1，这时我们的先验就变成了我们之前记录的${\alpha }_1(0)$和${\alpha }_1(1)$，它们分别表示了第一个状态为0/1的概率：

• 如果第二个状态为0，可能由第一个状态为0/1转移而来，那么其概率为$P={\alpha }_1(0)\ast A_{00}+{\alpha }_1(1)\ast A_{10}$，然后再由状态0观测到黑球概率为$B_{01}$，综合起来概率为${\alpha }_2(0)=({\alpha }_1(0)\ast A_{00}+{\alpha }_1(1)\ast A_{10})\ast B_{01}$
• 同样的，如果第二个状态为1，可能由第一个状态为0/1转移而来，那么其概率为$P={\alpha }_1(0)\ast A_{01}+{\alpha }_1(1)\ast A_{11}$，然后再由状态1观测到黑球概率为$B_{11}$，综合起来概率为${\alpha }_2(1)=({\alpha }_1(0)\ast A_{01}+{\alpha }_1(1)\ast A_{11})\ast B_{11}$

这样我们就得到了前两个观测和状态组成的马尔科夫链的概率，我们重复上述步骤，一直到得到5个状态的马尔科夫链概率：

• ${\alpha }_5(0)=({\alpha }_4(0)\ast A_{00}+{\alpha }_1(1)\ast A_{10})\ast B_{00}$
• ${\alpha }_5(1)=({\alpha }_4(0)\ast A_{01}+{\alpha }_1(1)\ast A_{11})\ast B_{10}$

将这两个概率加起来，就得到了最终的，在模型参数$\lambda$下观测到x的概率$P(x|\lambda )={\alpha }_5(0)+{\alpha }_5(1)$

附录展示了完整的计算过程！

可以把这个过程化成一个树状图：

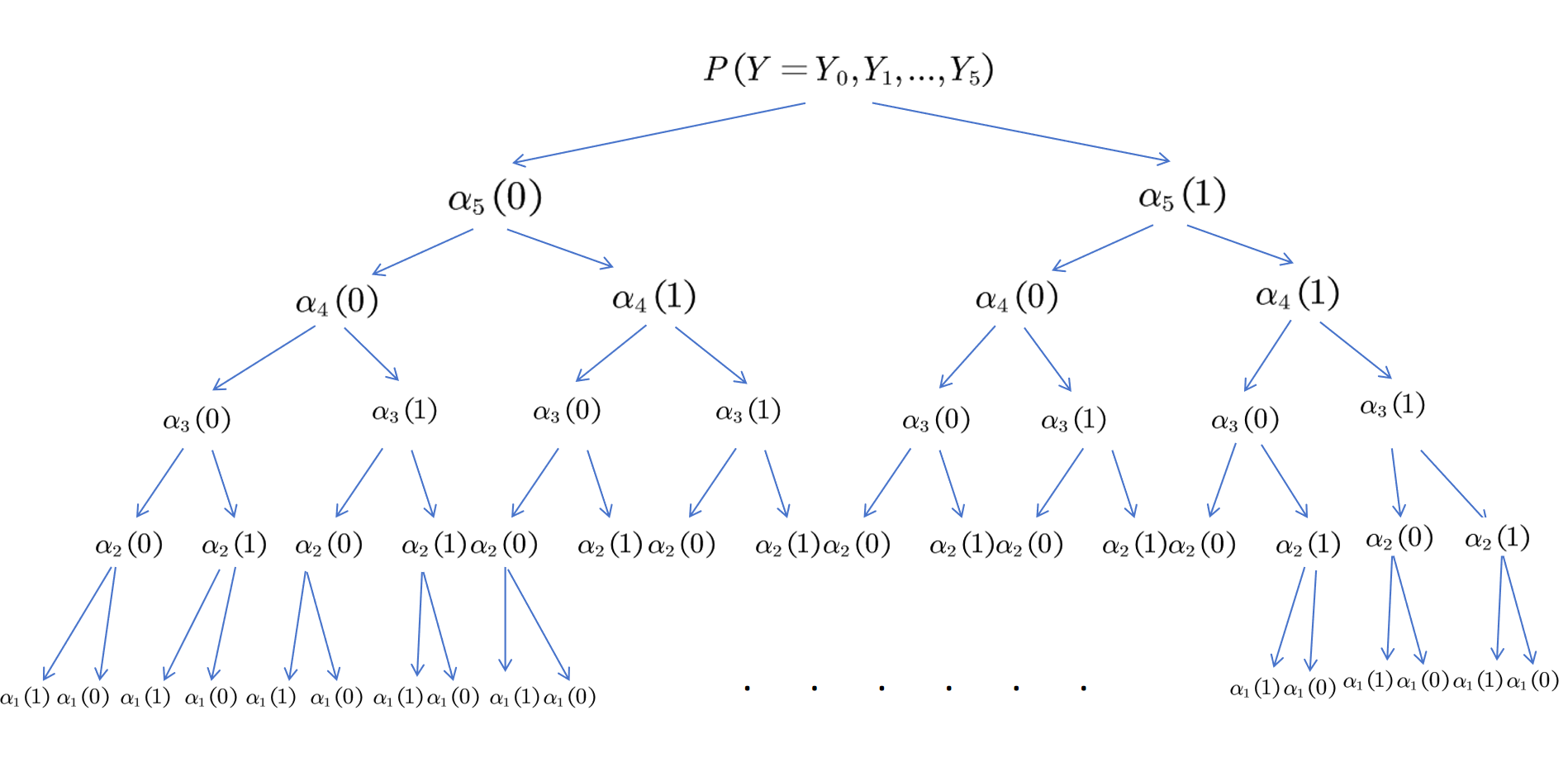
3.后向算法

后向算法，顾名思义就是从后往前算，我们先定义一个类似于$\alpha$的中间变量$\beta$，${\beta }_t(i)$表示：在t时刻的状态为i的条件下，从t+1时刻到n时刻(最后时刻)的部分观测变量$x_{t+1},x_{t+2},...,x_n$的概率。

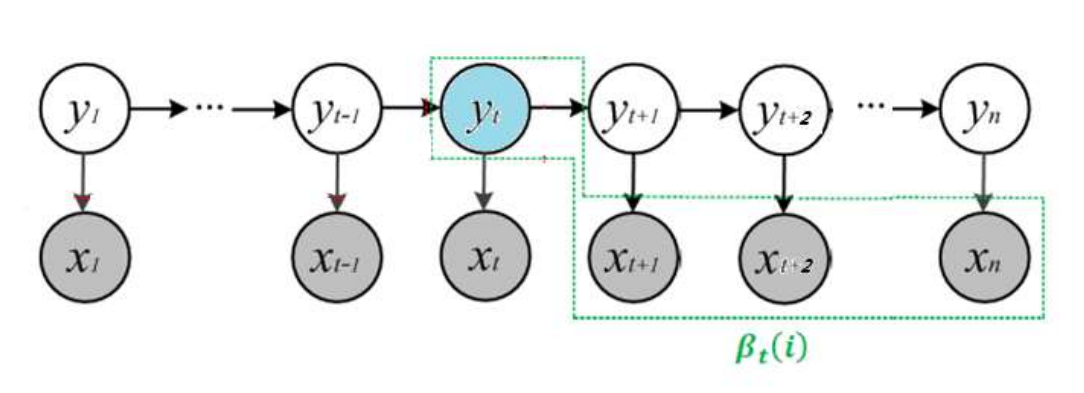
那么，我们现在开始逐步计算：

1. ${\beta }_5(0)$表示，假设第5个状态为0,得到6到最后观测的概率，因为一共5个状态，那么这个概率为1；同理${\beta }_5(1)=1$

2. ${\beta }_4(0)$表示，假设第4个状态为0,得到5到最后观测(第5个观测为红)的概率，第5个状态可能为0/1，那么我们应该这样计算${\beta }_4(0)=A_{00}\ast {\beta }_5(0)\ast B_{00}+A_{01}\ast {\beta }_5(1)\ast B_{01}$；同理，假设第4个状态为1，${\beta }_4(1)=A_{10}\ast B_{00}\ast {\beta }_5(0)+A_{11}\ast B_{11}\ast {\beta }_5(1)$

进一步解释：${\beta }_4(0)=A_{00}\ast {\beta }_5(0)\ast B_{00}$，表示第四个状态为0(\beta_4(0))，到第五个状态为0(A_{00}*\beta_5(0))，然后观测为红球(B_{00})

3. 依次从后向前计算，最后计算得到${\beta }_1(0)$和${\beta }_1(1)$，表示假设第1个状态为0或1,得到2到最后观测的概率，也就是得到了下图的马尔科夫链的概率。

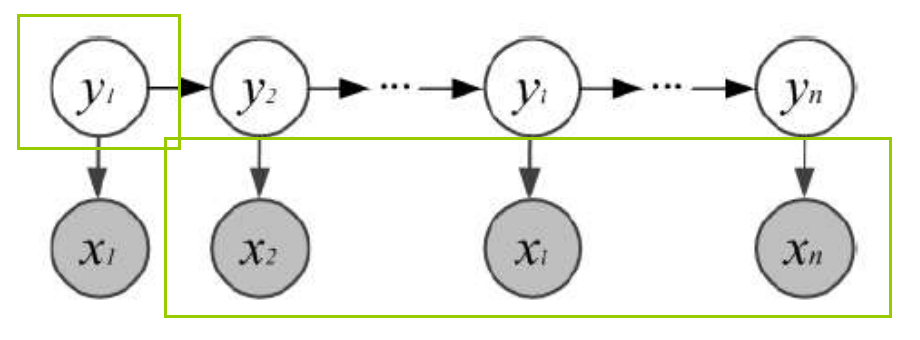
4. 这时，注意到还有第一个观测没有考虑进来，所以我们要再向前推一个，第0个状态(稳态先验)为0或1,得到1到最后观测的概率，第0的状态是不存在在马尔科夫链中的，我们用先验知识(稳态向量$\pi$)进行猜测，然后相加就得到了最终的概率

附录展示了完整的计算过程！

$$P(x|\lambda )=\pi (0)\ast B_{00}\ast {\beta }_1(0)+\pi (1)\ast B_{10}\ast {\beta }_1(1)$$

对应上面的树状图，前向算法相当于树自顶向下不断分叉，后向算法相当于自底向上不断合并，两个过程都可以得到最终的概率。

总结

现在我们已经掌握了，在给定隐马尔科夫链参数的条件下，如何计算获得当前观测的概率，对应这组观测序列，有很多可能得状态序列，比如：0,1,0,1,0;1,1,1,0,1;1,1,1,1,1等等，哪一条才是最有可能得到这组观测的状态序列呢？

这就是预测问题，我们将在下一篇文章介绍解决这个问题的经典算法-维特比算法。

附录