无穷级数（4）

本文讲解一些关于数项级数的习题。

1.

 条件收敛是说原级数收敛，但是它的绝对值级数发散，由无穷级数性质2知题中给出的两个级数都发散。

选B

2.

 记

, 由已知条件，原级数发散，它肯定不会绝对收敛，因此这两个部分和都无界；故C项级数的部分和肯定无界。

A、B项是根据之前的结论可以判错的，发散级数之和、积敛散性未知，要看具体情况，比如

B,取, 它们乘积的级数收敛；

A，取;

D项，取

3.

D项明显正确， 两个收敛级数的和仍收敛。

4. 

A项，未说明是正项级数，不能直接使用正项级数审敛法

B项，取 

C项，取

5.

6.

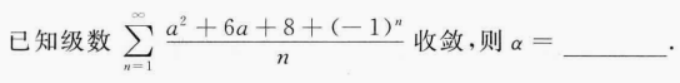
 我们知道，是收敛的，现在它加上另一个级数仍收敛，那么就要求这个加上的级数必须收敛；而当分子不为零时，这个级数是一个p级数，发散，因此分子必须为零。

7.

 选D。

A、C表示的条件很弱，不足以证明级数收敛；

B的前提是级数是一个正项级数，对于一般的级数而言，应该是其部分和数列收敛；

D项实际上就是柯西收敛原理的表述，正确。

柯西收敛原理表述如下：

8.

此题举反例如同即可，作为交错级数时，p不为零时，该级数都是收敛的；但是一旦由于加平方、加绝对值等操作让分子变成了1，这就是一个p级数，敛散性根据p来定。

 

应选D。